Introduction to Supercomputing

Overview

Teaching: 60 min
Exercises: 30 min

Topics

What is High-Performance Computing?

What is an HPC cluster or Supercomputer?

How does my computer compare with an HPC cluster?

Which are the main concepts in High-Performance Computing?

Objectives

Learn the components of the HPC

Learn the basic terminology in HPC

High-Performance Computing

In everyday life, we are doing calculations. Before paying for some items, we may be interested in the total price. For that, we can do the sum on our heads, on paper, or by using the calculator that is now integrated into today’s smartphones. Those are simple operations. To compute interest on a loan or mortgage, we could better use a spreadsheet or web application to calculate loans and mortgages. There are more demanding calculations like those needed for computing statistics for a project, fitting some experimental values to a theoretical function, or analyzing the features of an image. Modern computers are more than capable of these tasks, and many friendly software applications are capable of solving those problems with an ordinary computer.

Scientific computing consists of using computers to answer questions that require computational resources. Several of the examples given fit the definition of scientific computations. Experimental problems can be modeled in the framework of some theory. We can use known scientific principles to simulate the behavior of atoms, molecules, fluids, bridges, or stars. We can train computers to recognize cancer on images or cardiac diseases from electrocardiograms. Some of those problems could be beyond the capabilities of regular desktop and laptop computers. In those cases, we need special machines capable of processing all the necessary computations in a reasonable time to get the answers we expect.

When the known solution to a computational problem exceeds what you can typically do with a single computer, we are in the realm of Supercomputing, and one area in supercomputing is called High-Performance Computing (HPC).

There are supercomputers of the most diverse kinds. Some of them do not resemble at all what you can think about a computer. Those are machines designed from scratch for very particular tasks, all the electronics are specifically designed to run very efficiently a narrow set of calculations, and those machines could be as big as entire rooms.

However, there is a class of supercomputers made of machines relatively similar to regular computers. Regular desktop computers (towers) aggregated and connected with some network, such as Ethernet, were one of the first supercomputers built from commodity hardware. These clusters were instrumental in developing the cheaper supercomputers devoted to scientific computing and are called Beowulf clusters.

When more customized computers are used, those towers are replaced by slabs and positioned in racks. To increase the number of machines on the rack, several motherboards are sometimes added to a single chassis, and to improve performance, very fast networks are used. Those are what we understand today as HPC clusters.

In the world of HPC, machines are conceived based on the concepts of size and speed. The machines used for HPC are called Supercomputers, big machines designed to perform large-scale calculations. Supercomputers can be built for particular tasks or as aggregated or relatively common computers; in the latter case, we call those machines HPC clusters. An HPC cluster comprises tens, hundreds, or even thousands of relatively normal computers, especially connected to perform intensive computational operations and using software that makes these computers appear as a single entity rather than a network of independent machines.

Those computers are called nodes and can work independently of each other or together on a single job. In most cases, the kind of operations that supercomputers try to solve involves extensive numerical calculations that take too much time to complete and, therefore, are unfeasible to perform on an ordinary desktop computer or even the most powerful workstations.

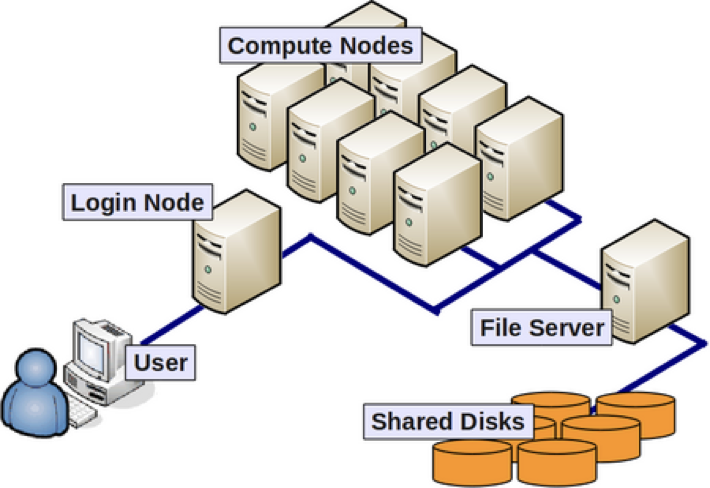
Anatomy of an HPC Cluster

The diagram above shows that an HPC cluster comprises several computers, here depicted as desktop towers. Still, in modern HPC clusters, those towers are replaced by computers that can be stacked into racks. All those computers are called nodes, the machines that execute your jobs are called “compute nodes,” and all other computers in charge of orchestration, monitoring, storage, and allowing access to users are called “infrastructure nodes.” Storage is usually separated into nodes specialized to read and write from large pools of drives, either mechanical drives (HDD), solid-state drives (SSD), or even a combination of both. Access to the HPC cluster is done via a special infrastructure node called the “login node.” A single login node is enough in clusters serving a relatively small number of users. Larger clusters with thousands of users can have several login nodes to balance the load.

Despite an HPC cluster being composed of several computers, the cluster itself should be considered an entity, i.e., a system. In most cases, you are not concerned about where your code is executed or whether one or two machines are online or offline. All that matters is the capacity of the system to process jobs, execute your calculations in one of the many resources available, and deliver the results in a storage that you can easily access.

What are the specifications of my computer?

One way of understanding what Supercomputing is all about is to start by comparing an HPC cluster with your desktop computer. This is a good way of understanding supercomputers’ scale, speed, and power.

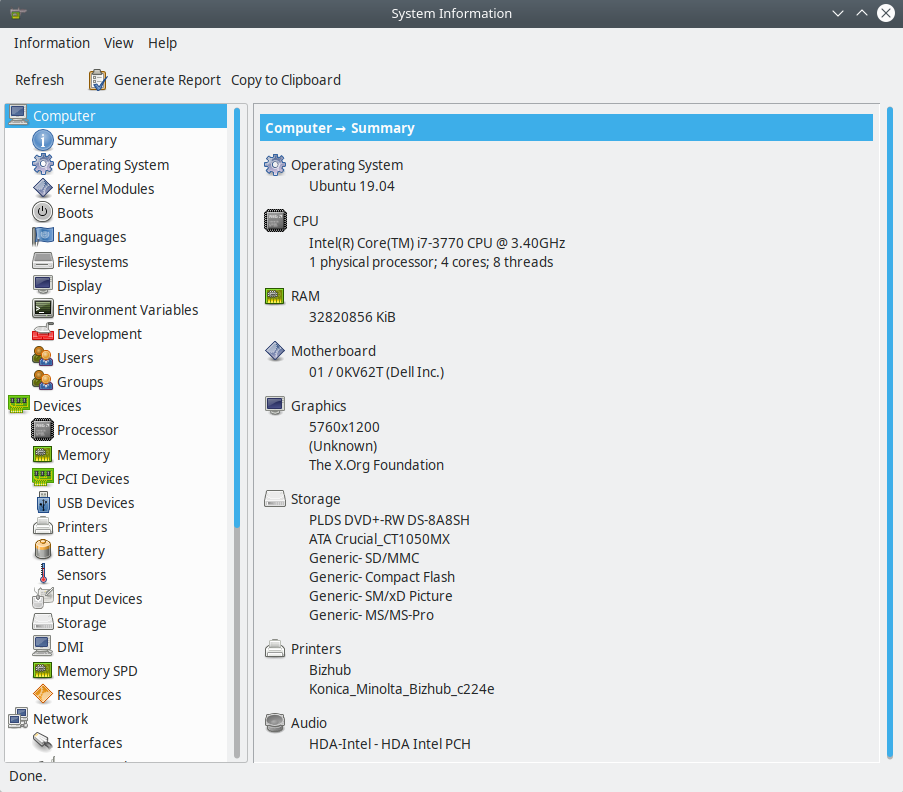
The first exercise consists of collecting critical information about the computer you have in front of you. We will use that information to identify the features of our HPC cluster. Gather information about the CPU, number of Cores, Total RAM, and Hard Drive from your computer.

You can see specs for our cluster Thorny Flat

Try to gather an idea of the Hardware present on your machine and see the hardware we have on Thorny Flat.

Here are some tricks to get that data from several Operating Systems

Open the File Explorer, search for the icon "This PC" click with the right mouse button and click properties. You should be able to see something like:

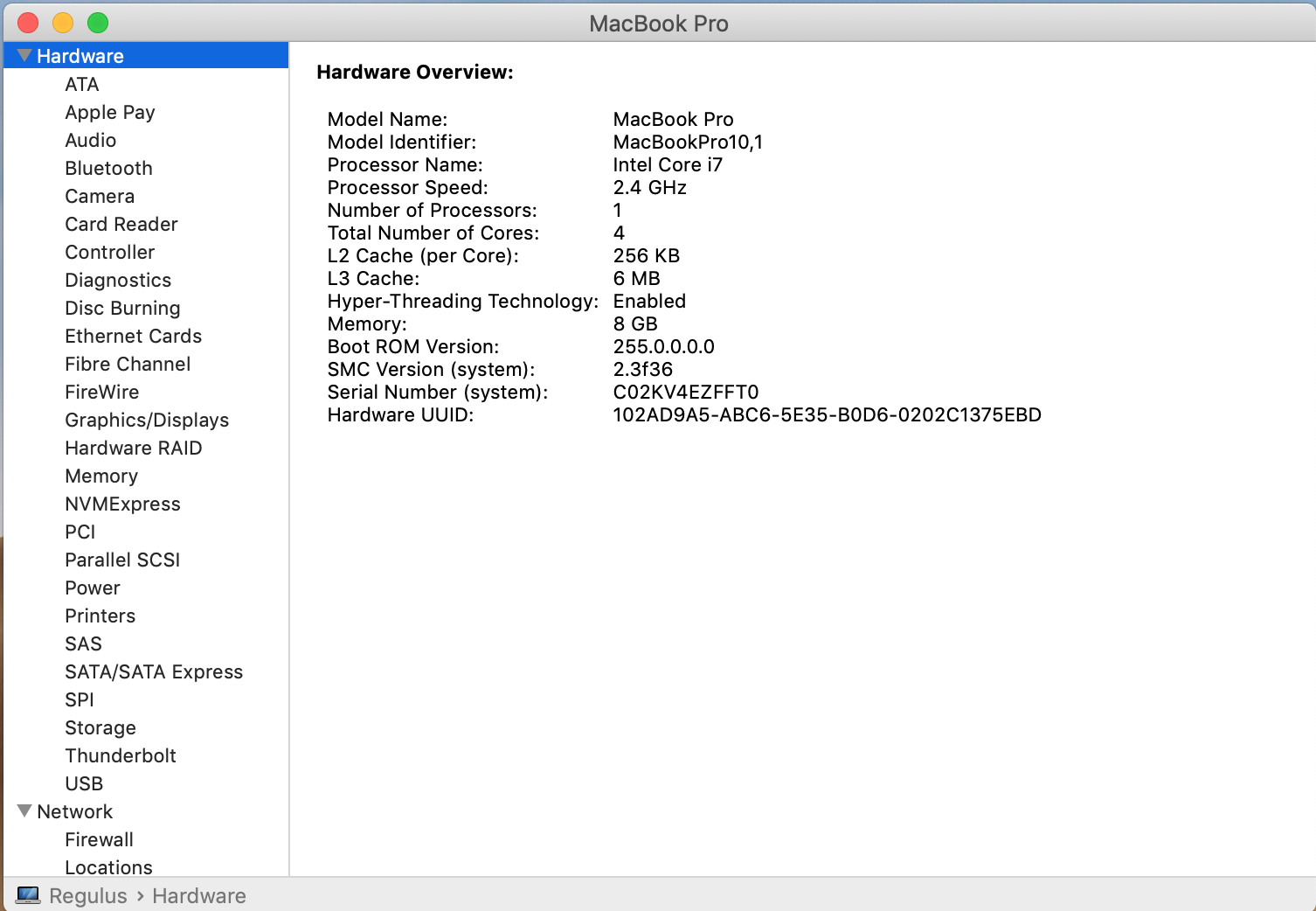
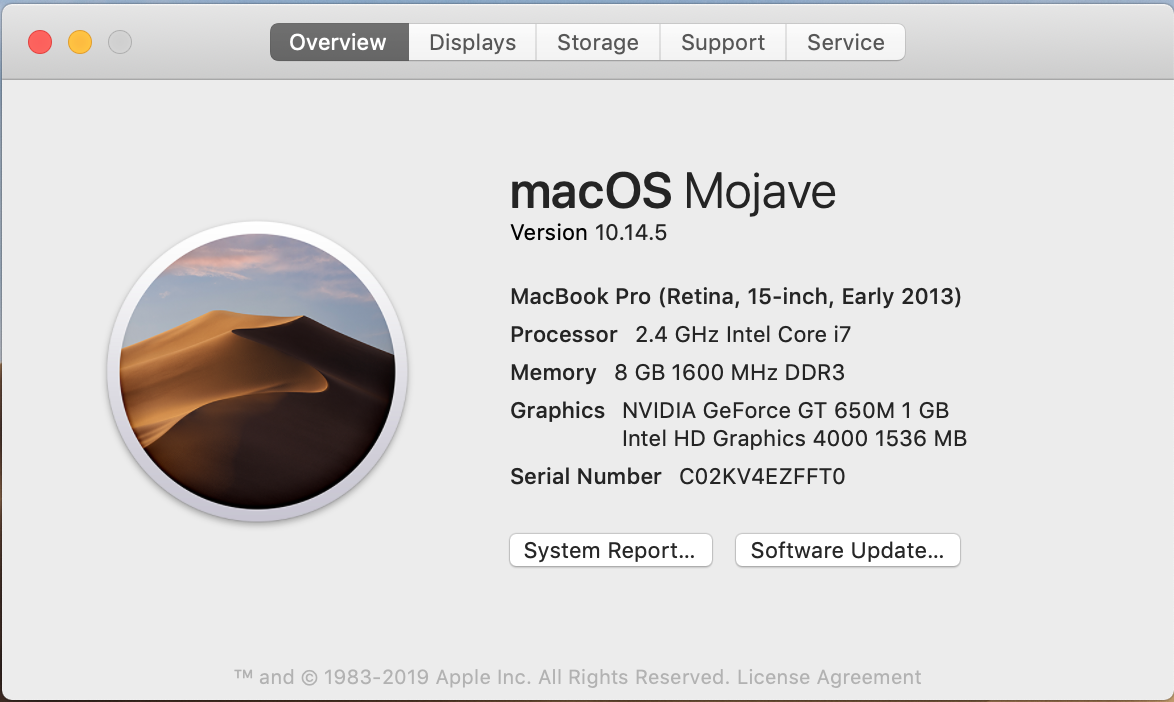On MacOS click on the top left corner (The Apple Icon), click on "About this Mac" and you will get the basic information.

If you want more data click on "System Report..." and you will get:

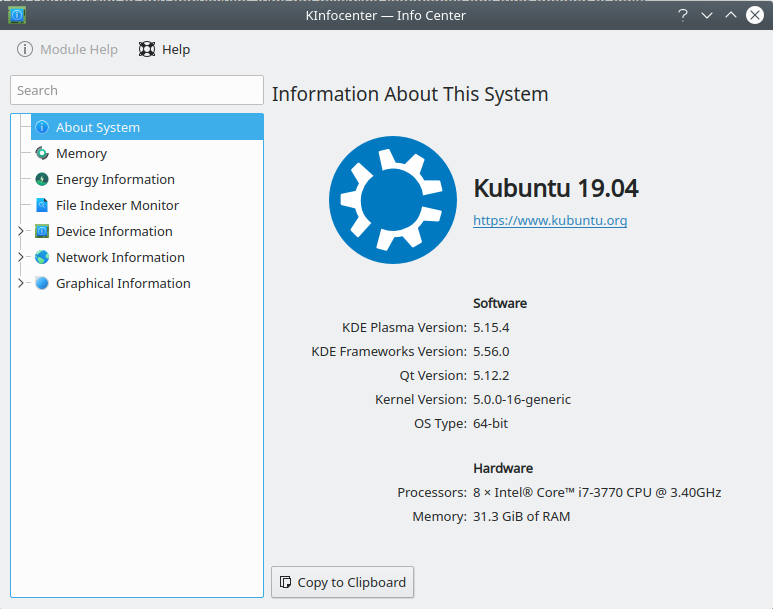
In Linux, gathering the data from a GUI depends much more on the exact distribution you use. Here are some tools that you can try:

KDE Info Center

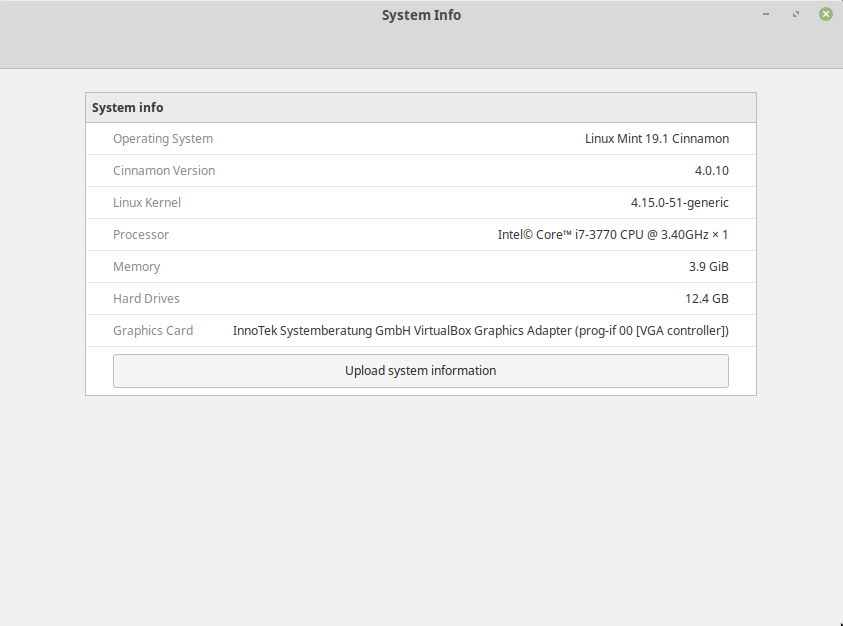
Linux Mint Cinnamon System Info

Advantages of using an HPC cluster for research

Using a cluster often has the following advantages for researchers:

Speed. An HPC cluster has many more CPU cores, often with higher performance specs, than a typical laptop or desktop, HPC systems can offer significant speed up.
Volume. Many HPC systems have processing memory (RAM) and disk storage to handle large amounts of data. Many GB of RAM and TeraBytes (TB) storage is available for research projects. Desktop computers rarely achieve the same amount of memory and storage.
Efficiency. Many HPC systems operate a pool of resources drawn on by many users. In most cases when the pool is large and diverse enough, the resources on the system are used almost constantly. A healthy HPC system usually achieves utilization on top of 80%. A normal desktop computer is idle for most of the day.
Cost. Bulk purchasing and government funding mean that the cost to the a research community for using these systems is significantly less than it would be otherwise. There are also economies done in terms of energy and human maintenance costs compared with desktop computers
Convenience. Maybe your calculations take a long time to run or are otherwise inconvenient to run on your personal computer. There’s no need to tie up your computer for hours when you can use someone else’s instead. Running on your machine could make it impossible to use it for other common tasks.

Compute nodes

On an HPC cluster, we have many machines, and each of them is a perfectly functional computer. It runs its copy of the Operating System, its mainboard, memory, and CPUs. All the internal components are the same as inside a desktop or laptop computer. The difference is subtle details like heat management systems, remote administration, subsystems to notify errors, special network storage devices, and parallel filesystems. All these subtle, important, and expensive differences make HPC clusters different from Beowulf clusters and normal PCs.

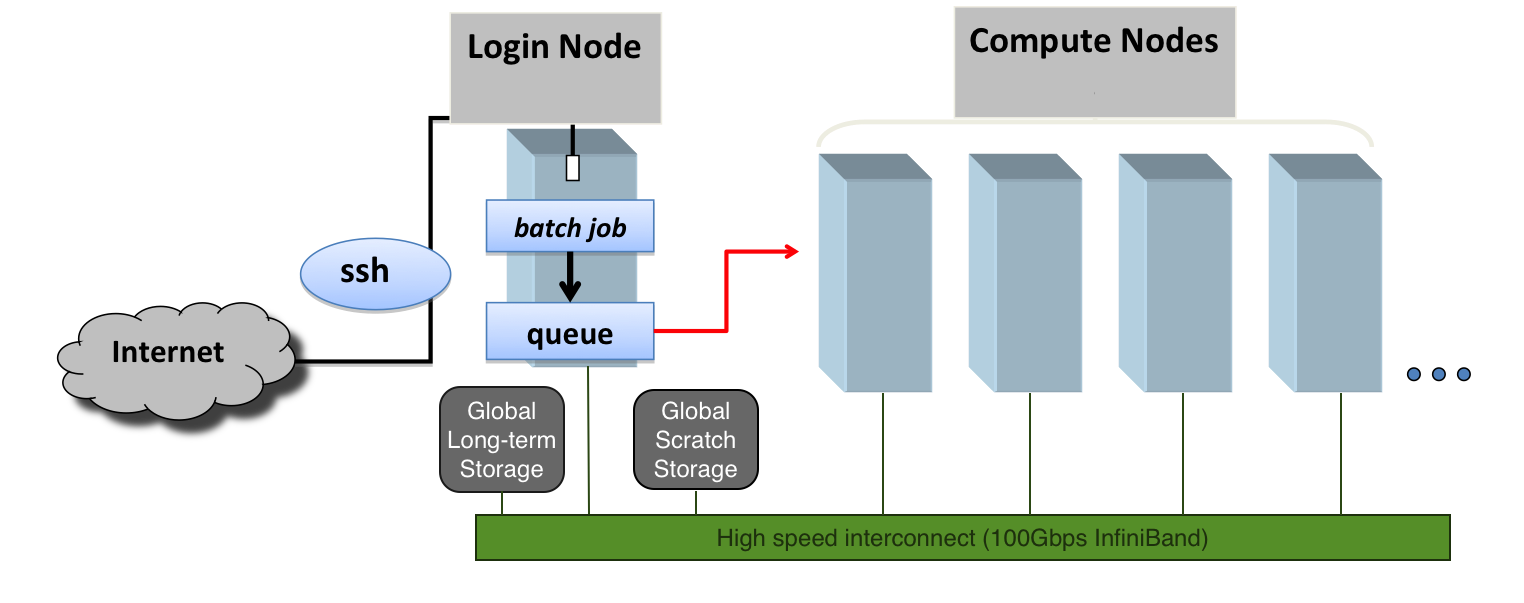
There are several kinds of computers in an HPC cluster. Most machines are used for running scientific calculations and are called Compute Nodes. A few machines are dedicated to administrative tasks, controlling the software that distributes jobs in the cluster, monitoring the health of all compute nodes, and interacting with the distributed storage devices. Among those administrative nodes, one or more are dedicated to be the front door to the cluster; they are called Head nodes. On HPC clusters with small to medium size, just one head node is enough; on larger systems, we can find several Head nodes, and you can end up connecting to one of them randomly to balance the load between them.

It would be best if you never ran intensive operations on the head node. Doing so will prevent the node from fulfilling its primary purpose, which is to serve other users, giving them access and allowing them to submit and manage the jobs running on the cluster. Instead of running on the head node, we use special software to submit jobs to the cluster, a queue system. We will discuss them later on in this lesson.

Central Processing Units

CPU Brands and Product lines

Only two manufacturers hold most of the market for PC consumer computing: Intel and AMD. Several other manufacturers of CPUs offer chips mainly for smartphones, Photo Cameras, Musical Instruments, and other very specialized Supercomputers and related equipment.

More than a decade ago, speed was the main feature used for marketing purposes on a CPU. That has changed as CPUs are not getting much faster due to faster clock speed. It is hard to market the performance of a new processor with a single number. That is why CPUs are now marketed with “Product Lines” and the “Model numbers.” Those numbers bear no direct relation to the actual characteristics of a given processor.

For example, Intel Core i3 processors are marketed for entry-level machines that are more tailored to basic computing tasks like word processing and web browsing. On the other hand, Intel’s Core i7 and i9 processors are for high-end products aimed at top-of-the-line gaming machines, which can run the most recent titles at high FPS and resolutions. Machines for enterprise usage are usually under the Xeon Line.

On AMD’s side, you have the Athlon line aimed at entry-level users, From Ryzen(TM) 3 for essential applications to the Ryzen(TM) 9, designed for enthusiasts and gamers. AMD also has product lines for enterprises like EPYC Server Processors.

Cores

Consumer-level CPUs up to the 2000s only had one core, but Intel and AMD hit a brick wall with incremental clock speed improvements. The heat and power consumption scales non-linearly with the CPU speed. That brings us to the current trend: CPUs now have two, three, four, eight, or sixteen cores on a single CPU instead of a single core. That means each CPU (in marketing terms) is several CPUs (in actual component terms).

There is a good metaphor, but I cannot claim it as mine, about CPUs, Cores, and Threads. The computer is like a Cooking Room; the cooking room could have one stove (CPUs) or several stoves (Dual Socket, for example). Each stove has multiple burners (Cores); you have multiple cookware like pans, casseroles, pots, etc (Threads). And you (OS) have to manage to cook all that in time, so you move the pan out of the burner to cook something else if needed and put it back to keep it warm.

Hyperthreading

Hyper-threading is intrinsically linked to cores and is best understood as a proprietary technology that allows the operating system to recognize the CPU as having double the number of cores.

In practical terms, a CPU with four physical cores would be recognized by the operating system as having eight virtual cores or capable of dealing with eight threads of execution. The idea is that by doing that, the CPU is expected to better manage the extra load by reordering execution and pipelining the workflow to the actual number of physical cores.

In the context of HPC, as loads are high for the CPU, activating hyper-threading is not necessarily beneficial for intensive numerical operations, and the question of whether that brings a benefit is very dependent on the scientific code and even the particular problem being solved. In our clusters, Hyper-threading is disabled on all compute nodes and enabled on service nodes.

CPU Frequency

Back in the 80s and 90s, CPU frequency was the most important feature of a CPU or at least that was how it was marketed.

Other names for CPU frequency are “clock rate”, or “clock speed”. CPUs work in steps instead of a continuous flow of information. Today, the speed of the CPU is measured in GHz, or how quickly the processor can process instructions in any given second (clock cycles per second). 1 Hz equals one cycle per second, so a 2 GHz frequency can handle 2 billion instructions for every second.

The higher the frequency, the more operations can be done. However, today that is not the whole story. Modern CPUs have complex CPU extensions (SSE, AVX, AVX2, and AVX512) that allow the CPU to execute several numerical operations on a single clock step.

On the other hand, CPUs can now change the speed up to certain limits, raising and lowering the value if needed. Sometimes raising the CPU frequency of a multicore CPU means that some cores are disabled.

One technique used to increase the performance of a CPU core is called overclocking. Overclocking is when the base frequency of a CPU is altered beyond the manufacturer’s official clock rate by user-generated means. In HPC, overclocking is not used, as doing so increases the chances of instability of the system. Stability is a well-regarded priority for a system intended for multiple users conducting scientific research.

Cache

The cache is a high-speed momentary memory device part of the CPU to facilitate future retrieval of data and instructions before processing. It’s very similar to RAM in that it acts as a temporary holding pen for data. However, CPUs access this memory in chunks, and the mapping to RAM is different.

Contrary to RAM, whose modules are independent hardware, cache sits on the CPU itself, so access times are significantly faster. The cache is an important portion of the production cost of a CPU, to the point where one of the differences between Intel’s main consumer lines, the Core i3s, i5s, and i7s, is the size of the cache memory.

There are several cache memories inside a CPU. They are called cache levels, or hierarchies, a bit like a pyramid: L1, L2, and L3. The lower the level the closer to the core.

From the HPC perspective, the cache size is an important feature for intensive numerical operations. Many CPU cycles are lost if you need to bring data all the time from the RAM or, even worse, from the Hard Drive. So, having large amounts of cache improves the efficiency of HPC codes. You, as an HPC user, must understand a bit about how cache works and impacts performance; however, users and developers have no direct control over the different cache levels.

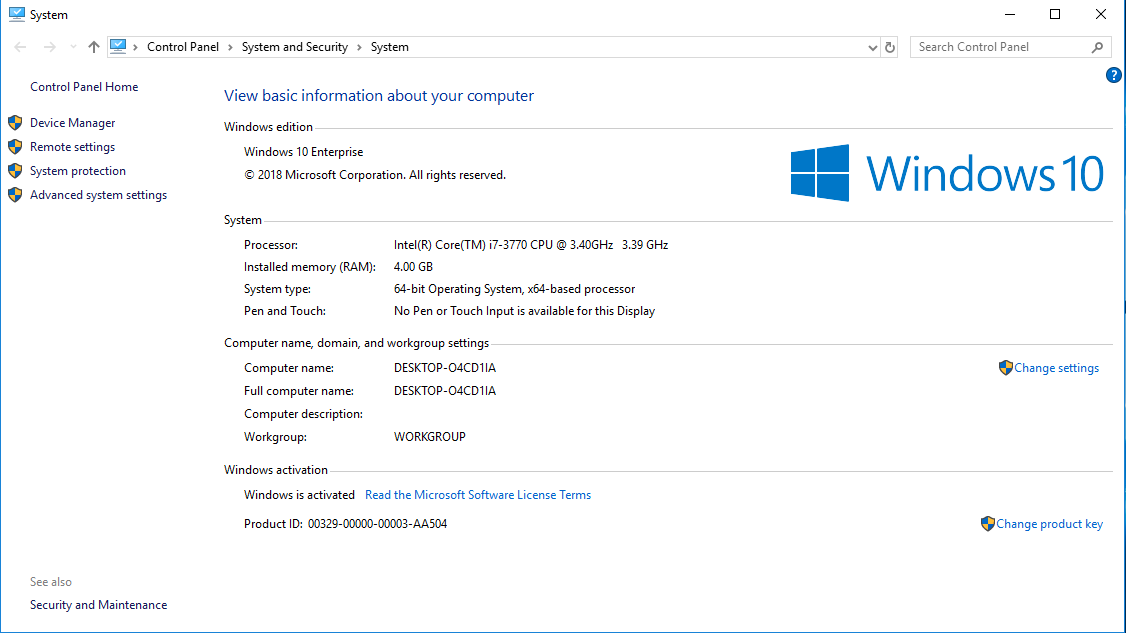
Learn to read computer specifications

One of the central differences between one computer and another is the CPU, the chip or set of chips that control most of the numerical operations. When reading the specifications of a computer, you need to pay attention to the amount of memory, whether the drive is SSD or not, the presence of a dedicated GPU card, and several factors that could or could not be relevant for your computer. Have a look at the CPU specifications on your machine.

Intel

If your machine uses Intel Processors, go to https://ark.intel.com and enter the model of CPU you have. Intel models are, for example: “E5-2680 v3”, “E5-2680 v3”

AMD

If your machine uses AMD processors, go to https://www.amd.com/en/products/specifications/processors and check the details for your machine.

Storage

Storage devices are another area where general supercomputers and HPC clusters differ from normal computers and consumer devices. On a normal computer, you have, in most cases, just one hard drive, maybe a few in some configurations, but that is all. Storage devices are measured by their capacity to store data and the speed at which the data can be written and retrieved from those devices. Today, hard drives are measured in GigaBytes (GB) and TeraBytes (TB). One Byte is a sequence of 8 bits, with a bit being a zero or one. One GB is roughly one billion (10^9) bytes, and a TB is about 1000 GB. Today, it is common to find Hard Drives with 8 or 16 TB per drive.

One HPC cluster’s special storage is needed. There are mainly three reasons for that: you need to store a far larger amount of data. A few TB is not enough; we need 100s of TB, maybe Peta Bytes, ie, 1000s of TB. The data is read and written concurrently by all the nodes on the machine. Speed and resilience is another important factor. For that reason, data is not stored; data is spread across multiple physical hard drives, allowing faster retrieval times and preserving the data in case one or more physical drives fail.

Network

Computers today connect to the internet or other computers via WiFI or Ethernet. Those connections are limited to a few GB/s too slow for HPC clusters where compute nodes need to exchange data for large computational tasks performed by multiple compute nodes simultaneously.

On HPC clusters, we find very specialized networks that are several times faster than Ethernet in several respects. Two important concepts when dealing with data transfer are Band Width and Latency. Bandwidth is the ability to transfer data across a given medium. Latency relates to the obstruction that data faces before the first bit reaches the other end. Both elements are important in HPC data communication and are minimized by expensive network devices. Examples of network technologies in HPC are Infiniband and OmniPath.

WVU High-Performance Computer Clusters

West Virginia University has two main clusters: Thorny Flat and Dolly Sods, our newest cluster that is specialized in GPU computing.

Thorny Flat

Thorny Flat is a general-purpose HPC cluster with 178 compute nodes; most nodes have 40 CPU cores. The total CPU core count is 6516 cores. There are 47 NVIDIA GPU cards ranging from P6000, RTX6000, and A100.

Dolly Sods

Dolly Sods is our newest cluster, and it is specialized in GPU computing. It has 37 nodes and 155 NVIDIA GPU cards ranging from A30, A40 and A100. The total CPU core count is 1248.

Command Line

Using HPC systems often involves the use of a shell through a command line interface (CLI) and either specialized software or programming techniques. The shell is a program with the special role of having the job of running other programs rather than doing calculations or similar tasks itself. What the user types goes into the shell, which then figures out what commands to run and orders the computer to execute them. (Note that the shell is called “the shell” because it encloses the operating system in order to hide some of its complexity and make it simpler to interact with.) The most popular Unix shell is Bash, the Bourne Again SHell (so-called because it’s derived from a shell written by Stephen Bourne). Bash is the default shell on most modern implementations of Unix and in most packages that provide Unix-like tools for Windows.

Interacting with the shell is done via a command line interface (CLI) on most HPC systems. In the earliest days of computers, the only way to interact with early computers was to rewire them. From the 1950s to the 1980s most people used line printers. These devices only allowed input and output of the letters, numbers, and punctuation found on a standard keyboard, so programming languages and software interfaces had to be designed around that constraint and text-based interfaces were the way to do this. Typing-based interfaces are often called a command-line interface, or CLI, to distinguish it from a graphical user interface, or GUI, which most people now use. The heart of a CLI is a read-evaluate-print loop, or REPL: when the user types a command and then presses the Enter (or Return) key, the computer reads it, executes it, and prints its output. The user then types another command, and so on until the user logs off.

Learning to use Bash or any other shell sometimes feels more like programming than like using a mouse. Commands are terse (often only a couple of characters long), their names are frequently cryptic, and their output is lines of text rather than something visual like a graph. However, using a command line interface can be extremely powerful, and learning how to use one will allow you to reap the benefits described above.

Secure Connections

The first step in using a cluster is establishing a connection from our laptop to the cluster. When we are sitting at a computer (or standing, or holding it in our hands or on our wrists), we expect a visual display with icons, widgets, and perhaps some windows or applications: a graphical user interface, or GUI. Since computer clusters are remote resources that we connect to over slow or intermittent interfaces (WiFi and VPNs especially), it is more practical to use a command-line interface, or CLI, to send commands as plain text. If a command returns output, it is printed as plain text as well. The commands we run today will not open a window to show graphical results.

If you have ever opened the Windows Command Prompt or macOS Terminal, you have seen a CLI. If you have already taken The Carpentries’ courses on the UNIX Shell or Version Control, you have used the CLI on your local machine extensively. The only leap to be made here is to open a CLI on a remote machine, while taking some precautions so that other folks on the network can’t see (or change) the commands you’re running or the results the remote machine sends back. We will use the Secure SHell protocol (or SSH) to open an encrypted network connection between two machines, allowing you to send & receive text and data without having to worry about prying eyes.

SSH clients are usually command-line tools, where you provide the remote machine address as the only required argument. If your username on the remote system differs from what you use locally, you must provide that as well. If your SSH client has a graphical front-end, such as PuTTY or MobaXterm, you will set these arguments before clicking “connect.” From the terminal, you’ll write something like ssh userName@hostname, where the argument is just like an email address: the “@” symbol is used to separate the personal ID from the address of the remote machine.

When logging in to a laptop, tablet, or other personal device, a username, password, or pattern is normally required to prevent unauthorized access. In these situations, the likelihood of somebody else intercepting your password is low, since logging your keystrokes requires a malicious exploit or physical access. For systems like running an SSH server, anybody on the network can log in, or try to. Since usernames are often public or easy to guess, your password is often the weakest link in the security chain. Many clusters, therefore, forbid password-based login, requiring instead that you generate and configure a public-private key pair with a much stronger password. Even if your cluster does not require it, the next section will guide you through the use of SSH keys and an SSH agent to both strengthen your security and make it more convenient to log in to remote systems.

Exercise 1

Follow the instructions for connecting to the cluster. Once you are on Thorny, execute
$> lscpu
On your browser, go to https://ark.intel.com and enter the CPU model on the cluster’s head node.

Execute this command to know the amount of RAM on the machine.
$> lsmem

High-Performance Computing and Geopolitics

Western democracies are losing the global technological competition, including the race for scientific and research breakthroughs and the ability to retain global talent—crucial ingredients that underpin the development and control of the world’s most important technologies, including those that don’t yet exist.

The Australian Strategic Policy Institute (ASPI) released in 2023 a report studying the position of big powers in 44 critical areas of technology.

The report says that China’s global lead extends to 37 out of the 44 technologies. Those 44 technologies range from fields spanning defense, space, robotics, energy, the environment, biotechnology, artificial intelligence (AI), advanced materials, and key quantum technology areas.

From that report, the US still leads in High-Performance Computing. HPC is a critical enabler for innovation in other essential technologies and scientific discoveries. New materials, drugs, energy sources, and aerospace technologies. They all rely on simulations and modeling carried out with HPC clusters.

Key Points

Learn about CPUs, cores, and cache, and compare your machine with an HPC cluster.

Identify how an HPC cluster could benefit your research.

Command Line Interface

Overview

Teaching: 60 min
Exercises: 30 min

Topics

How do I use the Linux terminal?

Objectives

Commands to connect to the HPC

Navigating the filesystem

Creating, moving, and removing files/directories

Command Line Interface

At a high level, an HPC cluster is a computer that several users can use simultaneously. The users expect to run a variety of scientific codes. To do that, users store the data needed as input, and at the end of the calculations, the data generated as output is also stored or used to create plots and tables via postprocessing tools and scripts. In HPC, compute nodes can communicate with each other very efficiently. For some calculations that are too demanding for a single computer, several computers could work together on a single calculation, eventually sharing information.

Our daily interactions with regular computers like desktop computers and laptops occur via various devices, such as the keyboard and mouse, touch screen interfaces, or the microphone when using speech recognition systems. Today, we are very used to interact with computers graphically, tablets, and phones, the GUI is widely used to interact with them. Everything takes place with graphics. You click on icons, touch buttons, or drag and resize photos with your fingers.

However, in HPC, we need an efficient and still very light way of communicating with the computer that acts as the front door of the cluster, the login node. We use the shell instead of a graphical user interface (GUI) for interacting with the HPC cluster.

In the GUI, we give instructions using a keyboard, mouse, or touchscreen. This way of interacting with a computer is intuitive and very easy to learn but scales very poorly for large streams of instructions, even if they are similar or identical. All that is very convenient but that is now how we use HPC clusters.

Later on in this lesson, we will show how to use Open On-demand, a web service that allows you to run interactive executions on the cluster using a web interface and your browser. For most of this lesson, we will use the Command Line Interface, and you need to familiarize yourself with it.

For example, you need to copy the third line of each of a thousand text files stored in a thousand different folders and paste it into a single file line by line. Using the traditional GUI approach of mouse clicks will take several hours to do this.

This is where we take advantage of the shell - a command-line interface (CLI) to make such repetitive tasks with less effort. It can take a single instruction and repeat it as is or with some modification as many times as we want. The task in the example above can be accomplished in a single line of a few instructions.

The heart of a command-line interface is a read-evaluate-print loop (REPL) so, called because when you type a command and press Return (also known as Enter), the shell reads your command, evaluates (or “executes”) it, prints the output of your command, loops back and waits for you to enter another command. The REPL is essential in how we interact with HPC clusters.

Even if you are using a GUI frontend such as Jupyter or RStudio, REPL is there for us to instruct computers on what to do next.

The Shell

The Shell is a program that runs other programs rather than doing calculations itself. Those programs can be as complicated as climate modeling software and as simple as a program that creates a new directory. The simple programs which are used to perform stand-alone tasks are usually referred to as commands. The most popular Unix shell is Bash (the Bourne Again SHell — so-called because it’s derived from a shell written by Stephen Bourne). Bash is the default shell on most modern implementations of Unix and in most packages that provide Unix-like tools for Windows.

When the shell is first opened, you are presented with a prompt, indicating that the shell is waiting for input.

The shell typically uses $ as the prompt but may use a different symbol like $>.

The prompt

When typing commands from these lessons or other sources, do not type the prompt, only the commands that follow it.
$> ls -al

Why use the Command Line Interface?

Before the usage of Command Line Interface (CLI), computer interaction took place with perforated cards or even switching cables on a big console. Despite all the years of new technology and innovation, the CLI remains one of the most powerful and flexible tools for interacting with computers.

Because it is radically different from a GUI, the CLI can take some effort and time to learn. A GUI presents you with choices to click on. With a CLI, the choices are combinations of commands and parameters, more akin to words in a language than buttons on a screen. Because the options are not presented to you, some vocabulary is necessary in this new “language.” But a small number of commands gets you a long way, and we’ll cover those essential commands below.

Flexibility and automation

The grammar of a shell allows you to combine existing tools into powerful pipelines and handle large volumes of data automatically. Sequences of commands can be written into a script, improving the reproducibility of workflows and allowing you to repeat them easily.

In addition, the command line is often the easiest way to interact with remote machines and supercomputers. Familiarity with the shell is essential to run a variety of specialized tools and resources including high-performance computing systems. As clusters and cloud computing systems become more popular for scientific data crunching, being able to interact with the shell is becoming a necessary skill. We can build on the command-line skills covered here to tackle a wide range of scientific questions and computational challenges.

Starting with the shell

If you still need to download the hands-on materials. This is the perfect opportunity to do so

$ git clone https://github.com/WVUHPC/workshops_hands-on.git

Let’s look at what is inside the workshops_hands-on folder and explore it further. First, instead of clicking on the folder name to open it and look at its contents, we have to change the folder we are in. When working with any programming tools, folders are called directories. We will be using folder and directory interchangeably moving forward.

To look inside the workshops_hands-on directory, we need to change which directory we are in. To do this, we can use the cd command, which stands for “change directory”.

$ cd workshops_hands-on

Did you notice a change in your command prompt? The “~” symbol from before should have been replaced by the string ~/workshops_hands-on$ . This means our cd command ran successfully, and we are now in the new directory. Let’s see what is in here by listing the contents:

$ ls

You should see:

Introduction_HPC  LICENSE  Parallel_Computing  README.md  Scientific_Programming  Spark

Arguments

Six items are listed when you run ls, but what types of files are they, or are they directories or files?

To get more information, we can modify the default behavior of ls with one or more “arguments”.

$ ls -F

Introduction_HPC/  LICENSE  Parallel_Computing/  README.md  Scientific_Programming/  Spark/

Anything with a “/” after its name is a directory. Things with an asterisk “*” after them are programs. If there are no “decorations” after the name, it’s a regular text file.

You can also use the argument -l to show the directory contents in a long-listing format that provides a lot more information:

$ ls -l

total 64
drwxr-xr-x 13 gufranco its-rc-thorny  4096 Jul 23 22:50 Introduction_HPC
-rw-r--r--  1 gufranco its-rc-thorny 35149 Jul 23 22:50 LICENSE
drwxr-xr-x  6 gufranco its-rc-thorny  4096 Jul 23 22:50 Parallel_Computing
-rw-r--r--  1 gufranco its-rc-thorny   715 Jul 23 22:50 README.md
drwxr-xr-x  9 gufranco its-rc-thorny  4096 Jul 23 22:50 Scientific_Programming
drwxr-xr-x  2 gufranco its-rc-thorny  4096 Jul 23 22:50 Spark

Each line of output represents a file or a directory. The directory lines start with d. If you want to combine the two arguments -l and -F, you can do so by saying the following:

ls -lF

Do you see the modification in the output?

Explanation

Notice that the listed directories now have / at the end of their names.

Tip - All commands are essentially programs that are able to perform specific, commonly-used tasks.

Most commands will take additional arguments controlling their behavior, and some will take a file or directory name as input. How do we know what the available arguments that go with a particular command are? Most commonly used shell commands have a manual available in the shell. You can access the manual using the man command. Let’s try this command with ls:

$ man ls

This will open the manual page for ls, and you will lose the command prompt. It will bring you to a so-called “buffer” page, a page you can navigate with your mouse, or if you want to use your keyboard, we have listed some basic keystrokes:

‘spacebar’ to go forward
‘b’ to go backward
Up or down arrows to go forward or backward, respectively

To get out of the man “buffer” page and to be able to type commands again on the command prompt, press the q key!

Exercise

Open up the manual page for the find command. Skim through some of the information.
- Would you be able to learn this much information about many commands by heart?
- Do you think this format of information display is useful for you?
Quit the man buffer and return to your command prompt.

Tip - Shell commands can get extremely complicated. No one can learn all of these arguments, of course. So you will likely refer to the manual page frequently.

Tip - If the manual page within the Terminal is hard to read and traverse, the manual exists online, too. Use your web-searching powers to get it! In addition to the arguments, you can also find good examples online; Google is your friend.

The Unix directory file structure (a.k.a. where am I?)

Let’s practice moving around a bit. Let’s go into the Introduction_HPC directory and see what is there.

$ cd Introduction_HPC

$ ls -l

Great, we have traversed some sub-directories, but where are we in the context of our pre-designated “home” directory containing the workshops_hands-on directory?!

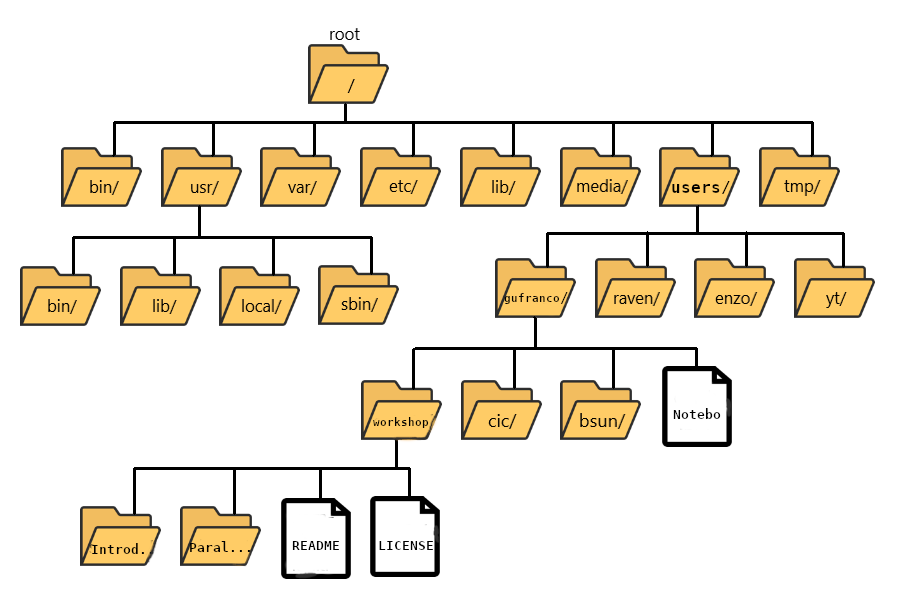
The “root” directory!

Like on any computer you have used before, the file structure within a Unix/Linux system is hierarchical, like an upside-down tree with the “/” directory, called “root” as the starting point of this tree-like structure:

Tip - Yes, the root folder’s actual name is just / (a forward slash).

That / or root is the ‘top’ level.

When you log in to a remote computer, you land on one of the branches of that tree, i.e., your pre-designated “home” directory that usually has your login name as its name (e.g. /users/gufranco).

Tip - On macOS, which is a UNIX-based OS, the root level is also “/”.

Tip - On a Windows OS, it is drive-specific; “C:" is considered the default root, but it changes to “D:", if you are on another drive.

Paths

Now let’s learn more about the “addresses” of directories, called “path”, and move around the file system.

Let’s check to see what directory we are in. The command prompt tells us which directory we are in, but it doesn’t give information about where the Introduction_HPC directory is with respect to our “home” directory or the / directory.

The command to check our current location is pwd. This command does not take any arguments, and it returns the path or address of your present working directory (the folder you are in currently).

$ pwd

In the output here, each folder is separated from its “parent” or “child” folder by a “/”, and the output starts with the root / directory. So, you are now able to determine the location of Introduction_HPC directory relative to the root directory!

But which is your pre-designated home folder? No matter where you have navigated to in the file system, just typing in cd will bring you to your home directory.

$ cd

What is your present working directory now?

$ pwd

This should now display a shorter string of directories starting with root. This is the full address to your home directory, also referred to as “full path”. The “full” here refers to the fact that the path starts with the root, which means you know which branch of the tree you are on in reference to the root.

Take a look at your command prompt now. Does it show you the name of this directory (your username?)?

No, it doesn’t. Instead of the directory name, it shows you a ~.

Why is this so?

This is because ~ = full path to the home directory for the user.

Can we just type ~ instead of /users/username?

Yes, we can!

Using paths with commands

You can do much more with the idea of stringing together parent/child directories. Let’s say we want to look at the contents of the Introduction_HPC folder but do it from our current directory (the home directory. We can use the list command and follow it up with the path to the folder we want to list!

$ cd

$ ls -l ~/workshops_hands-on/Introduction_HPC

Now, what if we wanted to change directories from ~ (home) to Introduction_HPC in a single step?

$ cd ~/workshops_hands-on/Introduction_HPC

Done! You have moved two levels of directories in one command.

What if we want to move back up and out of the Introduction_HPC directory? Can we just type cd workshops_hands-on? Try it and see what happens.

Unfortunately, that won’t work because when you say cd workshops_hands-on, shell is looking for a folder called workshops_hands-on within your current directory, i.e. Introduction_HPC.

Can you think of an alternative?

You can use the full path to workshops_hands-on!

$ cd ~/workshops_hands-on

Tip What if we want to navigate to the previous folder but can’t quite remember the full or relative path, or want to get there quickly without typing a lot? In this case, we can use cd -. When - is used in this context it is referring to a special variable called $OLDPWD that is stored without our having to assign it anything. We’ll learn more about variables in a future lesson, but for now you can see how this command works. Try typing:
cd -
This command will move you to the last folder you were in before your current location, then display where you now are! If you followed the steps up until this point it will have moved you to ~/workshops_hands-on/Introduction_HPC. You can use this command again to get back to where you were before (~/workshops_hands-on) to move on to the Exercises.

Exercises

First, move to your home directory.
Then, list the contents of the Parallel_Computing directory within the workshops_hands-on directory.

Tab completion

Typing out full directory names can be time-consuming and error-prone. One way to avoid that is to use tab completion. The tab key is located on the left side of your keyboard, right above the caps lock key. When you start typing out the first few characters of a directory name, then hit the tab key, Shell will try to fill in the rest of the directory name.

For example, first type cd to get back to your home directly, then type cd uni, followed by pressing the tab key:

$ cd
$ cd work<tab>

The shell will fill in the rest of the directory name for workshops_hands-on.

Now, let’s go into Introduction_HPC, then type ls 1, followed by pressing the tab key once:

$ cd Introduction_HPC/
$ ls 1<tab>

Nothing happens!!

The reason is that there are multiple files in the Introduction_HPC directory that start with 1. As a result, shell needs to know which one to fill in. When you hit tab a second time again, the shell will then list all the possible choices.

$ ls 1<tab><tab>

Now you can select the one you are interested in listed, enter the number, and hit the tab again to fill in the complete name of the file.

$ ls 15._Shell<tab>

NOTE: Tab completion can also fill in the names of commands. For example, enter e<tab><tab>. You will see the name of every command that starts with an e. One of those is echo. If you enter ech<tab>, you will see that tab completion works.

Tab completion is your friend! It helps prevent spelling mistakes and speeds up the process of typing in the full command. We encourage you to use this when working on the command line.

Relative paths

We have talked about full paths so far, but there is a way to specify paths to folders and files without having to worry about the root directory. You used this before when we were learning about the cd command.

Let’s change directories back to our home directory and once more change directories from ~ (home) to Introduction_HPC in a single step. (Feel free to use your tab-completion to complete your path!)

$ cd
$ cd workshops_hands-on/Introduction_HPC

This time we are not using the ~/ before workshops_hands-on. In this case, we are using a relative path, relative to our current location - wherein we know that workshops_hands-on is a child folder in our home folder, and the Introduction_HPC folder is within workshops_hands-on.

Previously, we had used the following:
$ cd ~/workshops_hands-on/Introduction_HPC

There is also a handy shortcut for the relative path to a parent directory, two periods ... Let’s say we wanted to move from the Introduction_HPC folder to its parent folder.

cd ..

You should now be in the workshops_hands-on directory (check the command prompt or run pwd).

You will learn more about the .. shortcut later. Can you think of an example when this shortcut to the parent directory won’t work?

Answer

When you are at the root directory, since there is no parent to the root directory!

When using relative paths, you might need to check what the branches are downstream of the folder you are in. There is a really handy command (tree) that can help you see the structure of any directory.

$ tree

If you are aware of the directory structure, you can string together a list of directories as long as you like using either relative or full paths.

Synopsis of Full versus Relative paths

A full path always starts with a /, a relative path does not.

A relative path is like getting directions from someone on the street. They tell you to “go right at the Stop sign, and then turn left on Main Street”. That works great if you’re standing there together, but not so well if you’re trying to tell someone how to get there from another country. A full path is like GPS coordinates. It tells you exactly where something is, no matter where you are right now.

You can usually use either a full path or a relative path depending on what is most convenient. If we are in the home directory, it is more convenient to just enter the relative path since it involves less typing.

Over time, it will become easier for you to keep a mental note of the structure of the directories that you are using and how to quickly navigate among them.

Copying, creating, moving, and removing data

Now we can move around within the directory structure using the command line. But what if we want to do things like copy files or move them from one directory to another, rename them?

Let’s move into the Introduction_HPC directory, which contains some more folders and files:

cd ~/workshops_hands-on/Introduction_HPC
cd 2._Command_Line_Interface

Copying

Let’s use the copy (cp) command to make a copy of one of the files in this folder, Mov10_oe_1.subset.fq, and call the copied file Mov10_oe_1.subset-copy.fq. The copy command has the following syntax:

cp path/to/item-being-copied path/to/new-copied-item

In this case the files are in our current directory, so we just have to specify the name of the file being copied, followed by whatever we want to call the newly copied file.

$ cp OUTCAR OUTCAR_BKP

$ ls -l

The copy command can also be used for copying over whole directories, but the -r argument has to be added after the cp command. The -r stands for “recursively copy everything from the directory and its sub-directories”. We used it earlier when we copied over the workshops_hands-on directory to our home directories.

Creating

Next, let’s create a directory called ABINIT and we can move the copy of the input files into that directory.

The mkdir command is used to make a directory, syntax: mkdir name-of-folder-to-be-created.

$ mkdir ABINIT

Tip - File/directory/program names with spaces in them do not work well in Unix. Use characters like hyphens or underscores instead. Using underscores instead of spaces is called “snake_case”. Alternatively, some people choose to skip spaces and rather just capitalize the first letter of each new word (i.e. MyNewFile). This alternative technique is called “CamelCase”.

Moving

We can now move our copied input files into the new directory. We can move files around using the move command, mv, syntax:

mv path/to/item-being-moved path/to/destination

In this case, we can use relative paths and just type the name of the file and folder.

$ mv 14si.pspnc INCAR t17.files t17.in ABINIT/

Let’s check if the move command worked like we wanted:

$ ls -l ABINIT

Let us run abinit, this is a quick execution, and you have not yet learned how to submit jobs. So, for this exceptional time, we will execute this on the login node

cd ABINIT
$ module load atomistic/abinit/9.8.4_intel22_impi22 
$ mpirun -np 4 abinit < t17.files 

Renaming

The mv command has a second functionality, it is what you would use to rename files, too. The syntax is identical to when we used mv for moving, but this time instead of giving a directory as its destination, we just give a new name as its destination.

The files t17.out can be renamed, the ABINIT could run again with some change in the input. We want to rename that file:

$ mv t17.out t17.backup.out

$ ls

Tip - You can use mv to move a file and rename it simultaneously!

Important notes about mv:

When using mv, the shell will not ask if you are sure that you want to “replace existing file” or similar unless you use the -i option.
Once replaced, it is not possible to get the replaced file back!

Removing

We did not need to create a backup of our output as we noticed this file is no longer needed; in the interest of saving space on the cluster, we want to delete the contents of the t17.backup.out.

$ rm t17.backup.out

Important notes about rm

rm permanently removes/deletes the file/folder.
There is no concept of “Trash” or “Recycle Bin” on the command line. When you use rm to remove/delete, they’re really gone.
Be careful with this command!
You can use the -i argument if you want it to ask before removing rm -i file-name.

Let’s delete the ABINIT folder too. First, we’ll have to navigate our way to the parent directory (we can’t delete the folder we are currently in/using).

$ cd ..

$ rm  ABINIT

Did that work? Did you get an error?

Explanation

By default, rm, will NOT delete directories, but you use the -r flag if you are sure that you want to delete the directories and everything within them. To be safe, let's use it with the -i flag.

$ rm -ri ABINIT

-r: recursive, commonly used as an option when working with directories, e.g. with cp.
-i: prompt before every removal.

Exercise

Create a new folder in workshops_hands-on called abinit_test
Copy over the abinit inputs from 2._Command_Line_Interface to the ~/workshops_hands-on/Introduction_HPC/2._Command_Line_Interface/abinit_test folder
Rename the abinit_test folder and call it exercise1

Exiting from the cluster

To close the interactive session on the cluster and disconnect from the cluster, the command is exit. So, you are going to have to run the exit command twice.

00:11:05-gufranco@trcis001:~$ exit
logout
Connection to trcis001 closed.
guilleaf@MacBook-Pro-15in-2015 ~ %

10 Unix/Linux commands to learn and use

The `echo` and `cat` commands

The echo command is very basic; it returns what you give back to the terminal, kinda like an echo. Execute the command below.

$ echo "I am learning UNIX Commands"

I am learning UNIX Commands

This may not seem that useful right now. However, echo will also print the contents of a variable to the terminal. There are some default variables set for each user on the HPCs: $HOME is the pathway to the user’s “home” directory, and $SCRATCH is Similarly the pathway to the user’s “scratch” directory. More info on what those directories are for later, but for now, we can print them to the terminal using the echo command.

$ echo $HOME

/users/<username>

$ echo $SCRATCH

/scratch/<username>

In addition, the shell can do basic arithmetical operations, execute this command:

$ echo $((23+45*2))

Notice that, as customary in mathematics, products take precedence over addition. That is called the PEMDAS order of operations, ie "Parentheses, Exponents, Multiplication and Division, and Addition and Subtraction". Check your understanding of the PEMDAS rule with this command:

$ echo $(((1+2**3*(4+5)-7)/2+9))

Notice that the exponential operation is expressed with the ** operator. The usage of echo is important. Otherwise, if you execute the command without echo, the shell will do the operation and will try to execute a command called 42 that does not exist on the system. Try by yourself:

$ $(((1+2**3*(4+5)-7)/2+9))

-bash: 42: command not found

As you have seen before, when you execute a command on the terminal, in most cases you see the output printed on the screen. The next thing to learn is how to redirect the output of a command into a file. It will be very important to submit jobs later and control where and how the output is produced. Execute the following command:

$ echo "I am learning UNIX Commands." > report.log

With the character > redirects the output from echo into a file called report.log. No output is printed on the screen. If the file does not exist, it will be created. If the file existed previously, it was erased, and only the new contents were stored. In fact, > can be used to redirect the output of any command to a file!

To check that the file actually contains the line produced by echo, execute:

$ cat report.log

I am learning UNIX Commands.

The cat (concatenate) command displays the contents of one or several files. In the case of multiple files, the files are printed in the order they are described in the command line, concatenating the output as per the name of the command.

In fact, there are hundreds of commands, most of them with a variety of options that change the behavior of the original command. You can feel bewildered at first by a large number of existing commands, but most of the time, you will be using a very small number of them. Learning those will speed up your learning curve.

Folder commands

As mentioned, UNIX organizes data in storage devices as a tree. The commands pwd, cd and mkdir will allow you to know where you are, move your location on the tree, and create new folders. Later, we will learn how to move folders from one location on the tree to another.

The first command is pwd. Just execute the command on the terminal:

$ pwd

/users/<username>

It is always very important to know where in the tree you are. Doing research usually involves dealing with a large amount of data, and exploring several parameters or physical conditions. Therefore, organizing the filesystem is key.

When you log into a cluster, by default, you are located on your $HOME folder. That is why the pwd command should return that location in the first instance.

The following command cd is used to change the directory. A directory is another name for folder and is widely used; in UNIX, the terms are interchangeable. Other Desktop Operating Systems like Windows and MacOS have the concept of smart folders or virtual folders, where the folder that you see on screen has no correlation with a directory in the filesystem. In those cases, the distinction is relevant.

There is another important folder defined in our clusters, it’s called the scratch folder, and each user has its own. The location of the folder is stored in the variable $SCRATCH. Notice that this is internal convection and is not observed in other HPC clusters.

Use the next command to go to that folder:

$ cd $SCRATCH
$ pwd

/scratch/<username>

Notice that the location is different now; if you are using this account for the first time, you will not have files on this folder. It is time to learn another command to list the contents of a folder, execute:

$ ls

Assuming that you are using your HPC account for the first time, you will not have anything in your $SCRATCH folder and should therefore see no output from ls. This is a good opportunity to start your filesystem by creating one folder and moving into it, execute:

$ mkdir test_folder
$ cd test_folder

mkdir allows you to create folders in places where you are authorized to do so, such as your $HOME and $SCRATCH folders. Try this command:

$ mkdir /test_folder

mkdir: cannot create directory `/test_folder': Permission denied

There is an important difference between test_folder and /test_folder. The former is a location in your current directory, and the latter is a location starting on the root directory /. A normal user has no rights to create folders on that directory so mkdir will fail, and an error message will be shown on your screen.

Notice that we named it test_folder instead of test folder. In UNIX, there is no restriction regarding files or directories with spaces, but using them can become a nuisance on the command line. If you want to create the folder with spaces from the command line, here are the options:

$ mkdir "test folder with spaces"
$ mkdir another\ test\ folder\ with\ spaces

In any case, you have to type extra characters to prevent the command line application from considering those spaces as separators for several arguments in your command. Try executing the following:

$ mkdir another folder with spaces
$ ls

another folder with spaces  folder  spaces  test_folder  test folder with spaces  with

Maybe is not clear what is happening here. There is an option for ls that present the contents of a directory:

$ ls -l

total 0
drwxr-xr-x 2 myname mygroup 512 Nov  2 15:44 another
drwxr-xr-x 2 myname mygroup 512 Nov  2 15:45 another folder with spaces
drwxr-xr-x 2 myname mygroup 512 Nov  2 15:44 folder
drwxr-xr-x 2 myname mygroup 512 Nov  2 15:44 spaces
drwxr-xr-x 2 myname mygroup 512 Nov  2 15:45 test_folder
drwxr-xr-x 2 myname mygroup 512 Nov  2 15:45 test folder with spaces
drwxr-xr-x 2 myname mygroup 512 Nov  2 15:44 with

It should be clear, now what happens when the spaces are not contained in quotes "test folder with spaces" or escaped as another\ folder\ with\ spaces. This is the perfect opportunity to learn how to delete empty folders. Execute:

$ rmdir another
$ rmdir folder spaces with

You can delete one or several folders, but all those folders must be empty. If those folders contain files or more folders, the command will fail and an error message will be displayed.

After deleting those folders created by mistake, let's check the contents of the current directory. The command ls -1 will list the contents of a file one per line, something very convenient for future scripting:

$ ls -1

total 0
drwxr-xr-x 2 myname mygroup 512 Nov  2 15:45 another folder with spaces
drwxr-xr-x 2 myname mygroup 512 Nov  2 15:45 test_folder
drwxr-xr-x 2 myname mygroup 512 Nov  2 15:45 test folder with spaces

Commands for copy and move

The next two commands are cp and mv. They are used to copy or move files or folders from one location to another. In its simplest usage, those two commands take two arguments: the first argument is the source and the last one is the destination. In the case of more than two arguments, the destination must be a directory. The effect will be to copy or move all the source items into the folder indicated as the destination.

Before doing a few examples with cp and mv, let's use a very handy command to create files. The command touch is used to update the access and modification times of a file or folder to the current time. If there is no such file, the command will create a new empty file. We will use that feature to create some empty files for the purpose of demonstrating how to use cp and mv.

Let’s create a few files and directories:

$ mkdir even odd
$ touch f01 f02 f03 f05 f07 f11

Now, lets copy some of those existing files to complete all the numbers up to f11:

$ cp f03 f04
$ cp f05 f06
$ cp f07 f08
$ cp f07 f09
$ cp f07 f10

This is a good opportunity to present the * wildcard, and use it to replace an arbitrary sequence of characters. For instance, execute this command to list all the files created above:

$ ls f*

f01  f02  f03  f04  f05  f06  f07  f08  f09  f10  f11

The wildcard is able to replace zero or more arbitrary characters, for example:

$ ls f*1

f01  f11

There is another way of representing files or directories that follow a pattern, execute this command:

$ ls f0[3,5,7]

f03  f05  f07

The files selected are those whose last character is on the list [3,5,7]. Similarly, a range of characters can be represented. See:

$ ls f0[3-7]

f03  f04  f05  f06  f07

We will use those special characters to move files based on their parity. Execute:

$ mv f[0,1][1,3,5,7,9] odd
$ mv f[0,1][0,2,4,6,8] even

The command above is equivalent to executing the explicit listing of sources:

$ mv f01 f03 f05 f07 f09 f11 odd
$ mv f02 f04 f06 f08 f10 even

Delete files and Folders

As we mentioned above, empty folders can be deleted with the command rmdir, but that only works if there are no subfolders or files inside the folder that you want to delete. See for example, what happens if you try to delete the folder called odd:

$ rmdir odd

rmdir: failed to remove `odd': Directory not empty

If you want to delete odd, you can do it in two ways. The command rm allows you to delete one or more files entered as arguments. Let's delete all the files inside odd, followed by the deletion of the folder odd itself:

$ rm odd/*
$ rmdir odd

Another option is to delete a folder recursively, this is a powerful but also dangerous option. Quite unlike Windows/MacOS, recovering deleted files through a “Trash Can” or “Recycling Bin” does not happen in Linux; deleting is permanent. Let's delete the folder even recursively:

$ rm -r even

Summary of Basic Commands

The purpose of this brief tutorial is to familiarize you with the most common commands used in UNIX environments. We have shown ten commands that you will be using very often in your interaction. These 10 basic commands and one editor from the next section are all that you need to be ready to submit jobs on the cluster.

The next table summarizes those commands.

Command	Description	Examples
`echo`	Display a given message on the screen	`$ echo "This is a message"`
`cat`	Display the contents of a file on screen Concatenate files	`$ cat my_file`
`date`	Shows the current date on screen	`$ date` Sun Jul 26 15:41:03 EDT 2020
`pwd`	Return the path to the current working directory	`$ pwd` /users/username
`cd`	Change directory	`$ cd sub_folder`
`mkdir`	Create directory	`$ mkdir new_folder`
`touch`	Change the access and modification time of a file Create empty files	`$ touch new_file`
`cp`	Copy a file in another location Copy several files into a destination directory	`$ cp old_file new_file`
`mv`	Move a file in another location Move several files into a destination folder	`$ mv old_name new_name`
`rm`	Remove one or more files from the file system tree	`$ rm trash_file` `$ rm -r full_folder`

Exercise 1

Get into Thorny Flat with your training account and execute the commands ls, date, and cal

Exit from the cluster with exit

So let’s try our first command, which will list the contents of the current directory:
[training001@srih0001 ~]$ ls -al
total 64
drwx------   4 training001 training   512 Jun 27 13:24 .
drwxr-xr-x 151 root        root     32768 Jun 27 13:18 ..
-rw-r--r--   1 training001 training    18 Feb 15  2017 .bash_logout
-rw-r--r--   1 training001 training   176 Feb 15  2017 .bash_profile
-rw-r--r--   1 training001 training   124 Feb 15  2017 .bashrc
-rw-r--r--   1 training001 training   171 Jan 22  2018 .kshrc
drwxr-xr-x   4 training001 training   512 Apr 15  2014 .mozilla
drwx------   2 training001 training   512 Jun 27 13:24 .ssh
Command not found

If the shell can’t find a program whose name is the command you typed, it will print an error message such as:
$ ks
ks: command not found
Usually this means that you have mis-typed the command.

Exercise 2

Commands in Unix/Linux are very stable with some existing for decades now. This exercise begins to give you a feeling of the different parts of a command.

Execute the command cal, we executed the command before but this time execute it again like this cal -y. You should get an output like this:

[training001@srih0001 ~]$ cal -y

                         2021

January               February                 March
Su Mo Tu We Th Fr Sa   Su Mo Tu We Th Fr Sa   Su Mo Tu We Th Fr Sa
1  2       1  2  3  4  5  6       1  2  3  4  5  6
3  4  5  6  7  8  9    7  8  9 10 11 12 13    7  8  9 10 11 12 13
10 11 12 13 14 15 16   14 15 16 17 18 19 20   14 15 16 17 18 19 20
17 18 19 20 21 22 23   21 22 23 24 25 26 27   21 22 23 24 25 26 27
24 25 26 27 28 29 30   28                     28 29 30 31
31
April                   May                   June
Su Mo Tu We Th Fr Sa   Su Mo Tu We Th Fr Sa   Su Mo Tu We Th Fr Sa
1  2  3                      1          1  2  3  4  5
4  5  6  7  8  9 10    2  3  4  5  6  7  8    6  7  8  9 10 11 12
11 12 13 14 15 16 17    9 10 11 12 13 14 15   13 14 15 16 17 18 19
18 19 20 21 22 23 24   16 17 18 19 20 21 22   20 21 22 23 24 25 26
25 26 27 28 29 30      23 24 25 26 27 28 29   27 28 29 30
30 31
July                  August                September
Su Mo Tu We Th Fr Sa   Su Mo Tu We Th Fr Sa   Su Mo Tu We Th Fr Sa
1  2  3    1  2  3  4  5  6  7             1  2  3  4
4  5  6  7  8  9 10    8  9 10 11 12 13 14    5  6  7  8  9 10 11
11 12 13 14 15 16 17   15 16 17 18 19 20 21   12 13 14 15 16 17 18
18 19 20 21 22 23 24   22 23 24 25 26 27 28   19 20 21 22 23 24 25
25 26 27 28 29 30 31   29 30 31               26 27 28 29 30

October               November               December
Su Mo Tu We Th Fr Sa   Su Mo Tu We Th Fr Sa   Su Mo Tu We Th Fr Sa
1  2       1  2  3  4  5  6             1  2  3  4
3  4  5  6  7  8  9    7  8  9 10 11 12 13    5  6  7  8  9 10 11
10 11 12 13 14 15 16   14 15 16 17 18 19 20   12 13 14 15 16 17 18
17 18 19 20 21 22 23   21 22 23 24 25 26 27   19 20 21 22 23 24 25
24 25 26 27 28 29 30   28 29 30               26 27 28 29 30 31
31

Another very simple command that is very useful in HPC is date. Without any arguments, it prints the current date to the screen.

$ date

Sun Jul 26 15:41:03 EDT 2020

Exercise 3

Create two folders called one and two. In one create the empty file none1 and in two create > the empty file none2.

Create also in those two folders, files date1 and > date2 by redirecting the output from the command date > using >.
$ date > date1
Check with cat that those files contain dates.

Now, create the folders empty_files and dates and move > the corresponding files none1 and none2 to > empty_files and do the same for date1 and date2.

The folders one and two should be empty now; delete > them with rmdir Do the same with folders empty_files and dates with rm -r.

Exercise 4

The command line is powerful enough even to do programming. Execute the command below and see the answer.
[training001@srih0001 ~]$ n=1; while test $n -lt 10000; do  echo $n; n=`expr 2 \* $n`; done
1
2
4
8
16
32
64
128
256
512
1024
2048
4096
8192
If you are not getting this output check the command line very carefully. Even small changes could be interpreted by the shell as entirely different commands so you need to be extra careful and gather insight when commands are not doing what you want.

Now the challenge consists on tweaking the command line above to show the calendar for August for the next 10 years.

Hint

Use the command cal -h to get a summary of the arguments to show just one month for one specific year You can use expr to increase n by one on each cycle, but you can also use n=$(n+1)

Grabbing files from the internet

To download files from the internet, the absolute best tool is wget. The syntax is relatively straightforwards: wget https://some/link/to/a/file.tar.gz

Downloading the Drosophila genome

The Drosophila melanogaster reference genome is located at the following website: http://metazoa.ensembl.org/Drosophila_melanogaster/Info/Index. Download it to the cluster with wget.
cd to your genome directory
Copy this URL and paste it onto the command line:
$> wget ftp://ftp.ensemblgenomes.org:21/pub/metazoa/release-51/fasta/drosophila_melanogaster/dna/Drosophila_melanogaster.BDGP6.32.dna_rm.toplevel.fa.gz

Working with compressed files, using unzip and gunzip

The file we just downloaded is gzipped (has the .gz extension). You can uncompress it with gunzip filename.gz.

File decompression reference:

.tar.gz - tar -xzvf archive-name.tar.gz

.tar.bz2 - tar -xjvf archive-name.tar.bz2

.zip - unzip archive-name.zip

.rar - unrar archive-name.rar

.7z - 7z x archive-name.7z

However, sometimes we will want to compress files ourselves to make file transfers easier. The larger the file, the longer it will take to transfer. Moreover, we can compress a whole bunch of little files into one big file to make it easier on us (no one likes transferring 70000) little files!

The two compression commands we’ll probably want to remember are the following:

Compress a single file with Gzip - gzip filename

Compress a lot of files/folders with Gzip - tar -czvf archive-name.tar.gz folder1 file2 folder3 etc

Wildcards, shortcuts, and other time-saving tricks

Wild cards

The “*” wildcard:

Navigate to the ~/workshops_hands-on/Introduction_HPC/2._Command_Line_Interface/ABINIT directory.

The “*” character is a shortcut for “everything”. Thus, if you enter ls *, you will see all of the contents of a given directory. Now try this command:

$ ls 2*

This lists every file that starts with a 2. Try this command:

$ ls /usr/bin/*.sh

This lists every file in /usr/bin directory that ends in the characters .sh. “*” can be placed anywhere in your pattern. For example:

$ ls t17*.nc

This lists only the files that begin with ‘t17’ and end with .nc.

So, how does this actually work? The Shell (bash) considers an asterisk “*” to be a wildcard character that can match one or more occurrences of any character, including no character.

Tip - An asterisk/star is only one of the many wildcards in Unix, but this is the most powerful one, and we will be using this one the most for our exercises.

The “?” wildcard:

Another wildcard that is sometimes helpful is ?. ? is similar to * except that it is a placeholder for exactly one position. Recall that * can represent any number of following positions, including no positions. To highlight this distinction, lets look at a few examples. First, try this command:

$ ls /bin/d*

This will display all files in /bin/ that start with “d” regardless of length. However, if you only wanted the things in /bin/ that starts with “d” and are two characters long, then you can use:

$ ls /bin/d?

Lastly, you can chain together multiple “?” marks to help specify a length. In the example below, you would be looking for all things in /bin/ that start with a “d” and have a name length of three characters.

$ ls /bin/d??

Exercise

Do each of the following using a single ls command without navigating to a different directory.

List all of the files in /bin that start with the letter ‘c’
List all of the files in /bin that contain the letter ‘a’
List all of the files in /bin that end with the letter ‘o’

BONUS: Using one command to list all of the files in /bin that contain either ‘a’ or ‘c’. (Hint: you might need to use a different wildcard here. Refer to this post for some ideas.)

Shortcuts

There are some very useful shortcuts that you should also know about.

Home directory or “~”

Dealing with the home directory is very common. In the shell, the tilde character “~”, is a shortcut for your home directory. Let’s first navigate to the ABINIT directory (try to use tab completion here!):

$ cd
$ cd ~/workshops_hands-on/Introduction_HPC/2._Command_Line_Interface

Then enter the command:

$ ls ~

This prints the contents of your home directory without you having to type the full path. This is because the tilde “~” is equivalent to “/home/username”, as we had mentioned in the previous lesson.

Parent directory or “..”

Another shortcut you encountered in the previous lesson is “..”:

$ ls ..

The shortcut .. always refers to the parent directory of whatever directory you are currently in. So, ls .. will print the contents of unix_lesson. You can also chain these .. together, separated by /:

$ ls ../..

This prints the contents of /n/homexx/username, which is two levels above your current directory (your home directory).

Current directory or “.”

Finally, the special directory . always refers to your current directory. So, ls and ls . will do the same thing - they print the contents of the current directory. This may seem like a useless shortcut, but recall that we used it earlier when we copied over the data to our home directory.

To summarize, the commands ls ~ and ls ~/. do exactly the same thing. These shortcuts can be convenient when you navigate through directories!

Command History

You can easily access previous commands by hitting the arrow key on your keyboard. This way, you can step backward through your command history. On the other hand, the arrow key takes you forward in the command history.

Try it out! While on the command prompt, hit the arrow a few times, and then hit the arrow a few times until you are back to where you started.

You can also review your recent commands with the history command. Just enter:

$ history

You should see a numbered list of commands, including the history command you just ran!

Only a certain number of commands can be stored and displayed with the history command by default, but you can increase or decrease it to a different number. It is outside the scope of this workshop, but feel free to look it up after class.

NOTE: So far, we have only run very short commands that have very few or no arguments. It would be faster to just retype it than to check the history. However, as you start to run analyses on the command line, you will find that the commands are longer and more complex, and the history command will be very useful!

Cancel a command or task

Sometimes as you enter a command, you realize that you don’t want to continue or run the current line. Instead of deleting everything you have entered (which could be very long), you could quickly cancel the current line and start a fresh prompt with Ctrl + C.

$ # Run some random words, then hit "Ctrl + C". Observe what happens

Another useful case for Ctrl + C is when a task is running that you would like to stop. In order to illustrate this, we will briefly introduce the sleep command. sleep N pauses your command line from additional entries for N seconds. If we would like to have the command line not accept entries for 20 seconds, we could use:

$ sleep 20

While your sleep command is running, you may decide that in fact, you do want to have your command line back. To terminate the rest of the sleep command simply type:

Ctrl + C

This should terminate the rest of the sleep command. While this use may seem a bit silly, you will likely encounter many scenarios when you accidentally start running a task that you didn’t mean to start, and Ctrl + C can be immensely helpful in stopping it.

Other handy command-related shortcuts

Ctrl + A will bring you to the start of the command you are writing.
Ctrl + E will bring you to the end of the command.

Exercise

Checking the history command output, how many commands have you typed in so far?
Use the arrow key to check the command you typed before the history command. What is it? Does it make sense?
Type several random characters on the command prompt. Can you bring the cursor to the start with + ? Next, can you bring the cursor to the end with + ? Finally, what happens when you use + ?

Summary: Commands, options, and keystrokes covered

~           # home dir
.           # current dir
..          # parent dir
*           # wildcard
ctrl + c    # cancel current command
ctrl + a    # start of line
ctrl + e    # end of line
history

Advanced Bash Commands and Utilities

As you begin working more with the Shell, you will discover that there are mountains of different utilities at your fingertips to help increase command-line productivity. So far, we have introduced you to some of the basics to help you get started. In this lesson, we will touch on more advanced topics that can be very useful as you conduct analyses in a cluster environment.

Configuring your shell

In your home directory, there are two hidden files, .bashrc and .bash_profile. These files contain all the startup configuration and preferences for your command line interface and are loaded before your Terminal loads the shell environment. Modifying these files allows you to change your preferences for features like your command prompt, the colors of text, and add aliases for commands you use all the time.

NOTE: These files begin with a dot (.) which makes it a hidden file. To view all hidden files in your home directory, you can use:

$ ls -al ~/

`.bashrc` versus `.bash_profile`

You can put configurations in either file, and you can create either if it doesn’t exist. But why two different files? What is the difference?

The difference is that .bash_profile is executed for login shells, while .bashrc is executed for interactive non-login shells. It is helpful to have these separate files when there are preferences you only want to see on the login and not every time you open a new terminal window. For example, suppose you would like to print some lengthy diagnostic information about your machine (load average, memory usage, current users, etc) - the .bash_profile would be a good place since you would only want in displayed once when starting out.

Most of the time you don’t want to maintain two separate configuration files for login and non-login shells. For example, when you export a $PATH (as we had done previously), you want it to apply to both. You can do this by sourcing .bashrc from within your .bash_profile file. Take a look at your .bash_profile file, it has already been done for you:

$ less ~/.bash_profile

You should see the following lines:

if [ -f ~/.bashrc ]; then
   source ~/.bashrc
fi

What this means is that if a .bashrc files exist, all configuration settings will be sourced upon logging in. Any settings you would like applied to all shell windows (login and interactive) can simply be added directly to the .bashrc file rather than in two separate files.

Changing the prompt

In your file .bash_profile, you can change your prompt by adding this:

PS1="\[\033[35m\]\t\[\033[m\]-\[\033[36m\]\u\[\033[m\]@$HOST_COLOR\h:\[\033[33;1m\]\w\[\033[m\]\$ "
export PS1

You have yet to learn how to edit text files. Keep in mind that when you know how to edit files, you can test this trick. After editing the file, you need to source it or restart your terminal.

source ~/.bash_profile

Aliases

An alias is a short name that the shell translates into another (usually longer) name or command. They are typically placed in the .bash_profile or .bashrc startup files so that they are available to all subshells. You can use the alias built-in command without any arguments, and the shell will display a list of all defined aliases:

$ alias

This should return to you the list of aliases that have been set for you, and you can see the syntax used for setting an alias is:

alias aliasname=value

When setting an alias no spaces are permitted around the equal sign. If value contains spaces or tabs, you must enclose the value within quotation marks. ll is a common alias that people use, and it is a good example of this:

alias ll='ls -l'

Since we have a modifier -l and there is a space required, the quotations are necessary.

Let’s setup our own alias! Every time we want to start an interactive session we have type out this lengthy command. Wouldn’t it be great if we could type in a short name instead? Open up the .bashrc file using vim:

$ vim ~/.bashrc

Scroll down to the heading “# User specific aliases and functions,” and on the next line, you can set your alias:

alias sq='squeue --me'

Symbolic links

A symbolic link is a kind of “file” that is essentially a pointer to another file name. Symbolic links can be made to directories or across file systems with no restrictions. You can also make a symbolic link to a name that is not the name of any file. (Opening this link will fail until a file by that name is created.) Likewise, if the symbolic link points to an existing file which is later deleted, the symbolic link continues to point to the same file name even though the name no longer names any file.

The basic syntax for creating a symlink is:

ln -s /path/to/file /path/to/symlink

There is a scratch folder under the variable $SCRATCH. You can create a symbolic link to that location from your $HOME

And then we can symlink the files:

$ cd
$ ln -s $SCRATCH scratch

Now, if you check the directory where we created the symlinks, you should see the filenames listed in cyan text followed by an arrow pointing to the actual file location. (NOTE: If your files are flashing red text, this is an indication your links are broken so you might want to double check the paths.)

$ ll ~/scratch

Transferring files with `rsync`

When transferring large files or a large number of files, rsync is a better command to use. rsync employs a special delta transfer algorithm and a few optimizations to make the operation a lot faster. It will check file sizes and modification timestamps of both file(s) to be copied and the destination and skip any further processing if they match. If the destination file(s) already exists, the delta transfer algorithm will make sure only differences between the two are sent over.

There are many modifiers for the rsync command, but in the examples below, we only introduce a select few that we commonly use during file transfers.

Example 1:

rsync -t --progress /path/to/transfer/files/*.c /path/to/destination

This command would transfer all files matching the pattern *.c from the transfer directory to the destination directory. If any of the files already exist at the destination, then the rsync remote-update protocol is used to update the file by sending only the differences.

Example 2:

rsync -avr --progress /path/to/transfer/directory /path/to/destination

This command would recursively transfer all files from the transfer directory into the destination directory. The files are transferred in “archive” mode (-a), which ensures that symbolic links, devices, attributes, permissions, ownerships, etc., are preserved in the transfer. In both commands, we have additional modifiers for verbosity so we have an idea of how the transfer is progressing (-v, --progress)

NOTE: A trailing slash on the transfer directory changes the behavior to avoid creating an additional directory level at the destination. You can think of a trailing / as meaning “copy the contents of this directory” as opposed to “copy the directory by name”.

This lesson has been adapted from several sources, including the materials from the Harvard Chan Bioinformatics Core (HBC). These are open-access materials distributed under the terms of the Creative Commons Attribution license (CC BY 4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

The materials used in this lesson were also derived from work that is Copyright © Data Carpentry (http://datacarpentry.org/). All Data Carpentry instructional material is made available under the Creative Commons Attribution license (CC BY 4.0).
Adapted from the lesson by Tracy Teal. Original contributors: Paul Wilson, Milad Fatenejad, Sasha Wood, and Radhika Khetani for Software Carpentry (http://software-carpentry.org/)

Key Points

The basic commands you must know are echo, cat, date, pwd, cd, mkdir, touch, cp, mv, rm. You will use these commands very often.

Adjurn

Overview

Teaching: min
Exercises: min

Topics

Objectives

Use the break layout for placeholder episodes representing coffee breaks and lunches. These episodes do not have exercises, questions, objectives, or keypoints in their metadata, but must have a “break” field to show how long the break is (in minutes).

Key Points

Python Scripting for HPC

Overview

Teaching: 45 min
Exercises: 15 min

Topics

Why learn Python programming language?

How can I use Python to write small scripts?

Objectives

Learn about variables, loops, conditionals and functions

Python Programming for Scientists in a hurry

Chapter 1. Language Syntax

Guillermo Avendaño Franco
Aldo Humberto Romero

List of Notebooks

Python is a great general-purpose programming language on its own. Python is a general purpose programming language. It is interpreted and dynamically typed and is very suited for interactive work and quick prototyping while being powerful enough to write large applications in. The lesson is particularly oriented to Scientific Computing. Other episodes in the series include:

Language Syntax [This notebook]
Standard Library
Scientific Packages
NumPy
Matplotlib
SciPy
Pandas
Cython
Parallel Computing

After completing all the series in this lesson you will realize that python has become a powerful environment for scientific computing at several levels, from interactive computing to scripting to big project developments.

Setup

%load_ext watermark

%watermark

Last updated: 2024-07-25T19:09:53.181545-04:00

Python implementation: CPython
Python version       : 3.11.7
IPython version      : 8.14.0

Compiler    : Clang 12.0.0 (clang-1200.0.32.29)
OS          : Darwin
Release     : 20.6.0
Machine     : x86_64
Processor   : i386
CPU cores   : 8
Architecture: 64bit

import time
start = time.time()
chapter_number = 1
import matplotlib
%matplotlib inline
%load_ext autoreload
%autoreload 2

import numpy as np
import matplotlib.pyplot as plt

%watermark -iv

matplotlib: 3.8.2
numpy     : 1.26.2

Python Language Syntax

In this notebook we explore:

Introduction
Python Syntax I
1. Variables
2. Data Types
3. Mathematical Operations
Python Syntax II
1. Containers
2. Loops
3. Conditionals
Python Syntax III
1. Functions
Python Syntax IV
1. Classes
Differences between Python 2.x and 3.x
1. Print
2. Integer division

Introduction

Python is a multiparadigm, general-purpose, interpreted, high-level programming language. Python is **multiparadigm** because it supports multiple programming paradigms, including procedural, object-oriented, and functional programming. Python is dynamically typed and garbage-collected and due to its comprehensive standard library, Python is a **general purpose** language often described as a having the " batteries included" Python is an **interpreted** language, which precludes the need to compile code before executing a program because Python does the compilation in the background. Because Python is a **high-level programming language**, it abstracts many sophisticated details from the programming code. Python focuses so much on this abstraction that its code can be understood by most novice programmers. Python was conceived in the late 1980s by Guido van Rossum at Centrum Wiskunde \& Informatica (CWI) in the Netherlands as a successor to the ABC language (itself inspired by SETL), capable of exception handling and interfacing with the Amoeba operating system. Its implementation began in December 1989. Van Rossum continued as Python's lead developer until July 12, 2018, when he announced his "permanent vacation" from his responsibilities as Python's **Benevolent Dictator For Life (BDFL)**, a title the Python community bestowed upon him to reflect his long-term commitment as the project's chief decision-maker. In January 2019, active Python core developers elected Brett Cannon, Nick Coghlan, Barry Warsaw, Carol Willing, and Van Rossum to a five-member " Steering Council" to lead the project. Guido named his language Python as a tribute to the British comedy group Monty Python and not a reference to reptiles. However, logos and other media use stylized versions of reptiles. One consequence of the Monty Python original reference, tutorials and examples refer to spam and eggs (from a famous Monty Python sketch) instead of the standard foo and bar. The official language website is https://www.python.org.

Zen of Python

Python

users refer frequently Python philosophy. These principles of philosophy were written by the Python developer, Tim Peters, in the Zen of Python:

Zen of Python

Beautiful is better than ugly.
Explicit is better than implicit.
Simple is better than complex.
Complex is better than complicated.
Flat is better than nested.
Sparse is better than dense.
Readability counts.
Special cases aren't special enough to break the rules.
Although practicality beats purity.
Errors should never pass silently.
Unless explicitly silenced.
In the face of ambiguity, refuse the temptation to guess.
There should be one-- and preferably only one --obvious way to do it.
Although that way may not be obvious at first unless you're Dutch.
Now is better than never.
Although never is often better than *right* now.
If the implementation is hard to explain, it's a bad idea.
If the implementation is easy to explain, it may be a good idea.
Namespaces are one honking great idea -- let's do more of those!

Python in bulleted lists

Key characteristics of Python:

clean and simple language: (KISS principle) Easy-to-read and intuitive code, minimalist syntax, scales well with projects.
expressive language: Fewer lines of code, fewer bugs, easier to maintain.
multiparadigm: Including object-oriented, imperative, and functional programming or procedural styles.
standard library: Large and comprehensive set of functions that runs consistently where Python runs.

Technical details:

dynamically typed: No need to define the type of variables, function arguments, or return types.
automatic memory management: No need to explicitly allocate and deallocate memory for variables and data arrays (Like malloc in C).
interpreted: No need to compile the code. The Python interpreter reads and executes the python code directly.

Advantages

The main advantage is the ease of programming, minimizing the time required to develop, debug and maintain the code.
Well designed language that encourages many good programming practices:
Modular and object-oriented programming, a good system for packaging and re-use of code. This often results in more transparent, maintainable, and bug-free code.
Documentation tightly integrated with the code (Documentation is usually accessed by different means and depending on the interface used, such as scripting, notebooks, etc).
A large standard library, and a large collection of add-on packages.

Disadvantages

Since Python is an interpreted and dynamically typed programming language, the execution of python code can be slow compared to compiled statically typed programming languages, such as C and Fortran.
Lacks a standard GUI, there are several.
The current version of Python is 3.12.4 (July 2024). Since January 1, 2020, the older Python 2.x is no longer maintained. You should only use Python 3.x for all scientific purposes.

Optimizing what?

When we talk about programming languages we often ask about optimization. We hear that one code is more optimized than another. That one programming language is faster than another. That your work is more optimal using this or that tool, language, or technique.

The question here should be: What exactly do you want to optimize? The computer time (time that your code will be running on the machine) or the developer time (time you need to write the code) or the time waiting for results to be obtained ?

With low-level languages like C or Fortran, you can get codes that run very fast at expenses of long hours or code development and even more extensive hours of code debugging. Other languages are slower but you can progressively increase the performance by introducing changes in the code, using external libraries on critical sections, or using alternative interpreters that speed execution.

(from Johansson’s Scientific Python Lectures )

Python lies in the second category. It is easy to learn and fast to develop. It is not particularly fast but with the right tools you can increase its performance over time.

That is the reason why Python has a strong position in scientific computing. You start getting results very early during the development process. With time and effort, you can improve performance and get close to lower level programming languages.

On the other hand working with low-level languages like C or Fortran you have to write quite an amount of code to start getting the first results.

Programmer vs Scripter

You do not need to be a Python Programmer to use and take advantage of Python for your research. Have you ever found doing the same operation on a computer over and over again? simply because you do not know how to do it differently.

Scripts are not bad programs, they are simply quick and dirt, pieces of code that help you save your brain to better purposes. They are dirty because typically they are not commented, they are not actively maintained, no unitary tests, no continuous integration, no test farms, nothing of such things that first-class software usually relies on to remain functional over time.

For programs, there are those who write programs, integrated pieces of code that are intended to be used independently. Some write libraries, sets of functions, classes, routines, and methods, as you prefer to call them. Those are the building blocks of larger structures, such as programs or other libraries.

As a scientist that uses computing to pursue your research, you could be doing scripts, doing programs, or doing libraries. There is nothing pejorative in doing scripts, and there is nothing derogatory in using scripting languages. The important is the science, get the job done, and move forward.

In addition to Scripts and Programs, Python can be used in interactive computing. This document that you see right now was created as a Jupyter notebook. If you are reading it from an active Jupyter instance, you can execute these boxes.

Example 1: Program that converts from Fahrenheit to Celsius

Lets start with a simple example converting a variable that holds a value in Fahrenheit and convert it to Celsius

First code

f=80 # Temperature in F

c = 5/9 * (f-32)

print("The temperature of %.2f F is equal to %.2f C" % (f,c))

The temperature of 80.00 F is equal to 26.67 C

Second code

Now that we know how to convert from Fahrenheit to Celsius we can put the formula inside a function. Even better we want to write two functions, one to convert from F to C and the other to convert from C to F.

def fahrenheit2celsius(f):
    return 5/9 * (f-32)

def celsius2fahrenheit(c):
    return c*9/5 + 32

With this two functions we can use them to convert temperatures between these units.

fahrenheit2celsius(80)

26.666666666666668

celsius2fahrenheit(27)

80.6

We have learned here the use of variables, the print function and how to write functions in Python.

Testing your Python Environment

We will now explore a little bit about how things work in python. The purpose of this section is two-fold, to give you a quick overview of the kind of things that you can do with Python and to test if those things work for you, in particular the external libraries that could still not be present in your system. The most basic thing you can do is use the Python interpreter as a calculator, and test for example a simple operation to count the number of days on a non-leap year:

31*7 + 30*4 + 28

Python provides concise methods for handling lists without explicit use of loops.

They are called list comprehension, we will discuss them in more detail later on. I search for a very obfuscating case indeed!

n = 100 
primes = [prime for prime in range(2, n) if prime not in 
          [noprimes for i in range(2, int(n**0.5)) for noprimes in 
           range(i * 2, n, i)]]
print(primes)

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]

Python’s compact syntax: The quicksort algorithm

Python is a high-level, dynamically typed multiparadigm programming language. Python code is often said to be almost like pseudocode since it allows you to express very powerful ideas in very few lines of code while being very readable.

The quicksort algorithm is a classical algorithm for sorting a list of values. Developed by British computer scientist Tony Hoare in 1959 and published in 1961, quicksort is still a commonly used algorithm for sorting. When implemented well, it can be about two or three times faster than its main competitors, merge sort and heapsort. The steps to sort a list are these: 1. Choose any element of the array to be the pivot. 2. Divide all other elements (except the pivot) into two partitions. 3. All elements less than the pivot must be in the first partition. 4. All elements greater than the pivot must be in the second partition. 5. Use recursion to sort both partitions. 6. Join the first sorted partition, the pivot, and the second sorted partition.

As an example, here is an implementation of the classic quicksort algorithm in Python:

def quicksort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quicksort(left) + middle + quicksort(right)

print(quicksort([3,6,8,10,1,2,1]))

[1, 1, 2, 3, 6, 8, 10]

As comparison look for an equivalent version of the same algorithm implemented in C, based on a similar implementation on RosettaCode #include

void quicksort(int *A, int len);

int main (void) { int a[] = {3,6,8,10,1,2,1}; int n = sizeof a / sizeof a[0];

int i; for (i = 0; i < n; i++) { printf(“%d “, a[i]); } printf(“\n”);

quicksort(a, n);

for (i = 0; i < n; i++) { printf(“%d “, a[i]); } printf(“\n”);

return 0; }

void quicksort(int *A, int len) { if (len < 2) return;

int pivot = A[len / 2];

int i, j; for (i = 0, j = len - 1; ; i++, j–) { while (A[i] < pivot) i++; while (A[j] > pivot) j–;

if (i >= j) break;
 
int temp = A[i];
A[i]     = A[j];
A[j]     = temp;   }

quicksort(A, i); quicksort(A + i, len - i); } The most important benefits of Python is how compact the notation can be and how easy it is to write code that otherwise requires not only more coding, but also compilation.

Python, however, is in general much slower than C or Fortran. There are ways to alleviate this as we will see when we start using libraries like NumPy or external code translators like Cython.

Python versions

Today, Python 3.x is the only version actively developed and maintained. Before 2020 two versions were used the older Python 2 and the newer Python 3. Python 3 introduced many backward-incompatible changes to the language, so code is written for 2.x, in general, did not work under 3.x and vice versa.

By the time of writing this notebook (July 2022), the current version of Python is 3.10.5.

Python 2.7 is no longer maintained and you should avoid using Python 2.x for any purpose that pretends to be used by you or others in the future.

You can check your Python version at the command line by running on the terminal:

$> python --version
Python 3.10.5

Another way of checking the version from inside the Jupyter notebook like this is using:

import sys
print(sys.version)

3.11.7 (main, Dec 24 2023, 07:47:18) [Clang 12.0.0 (clang-1200.0.32.29)]

To get this we import a module called sys. This is just one of the many modules in the Python Standard Library. The Python standard library that is always distributed with Python. This library contains built-in modules (written in C) that provide access to system functionality such as file I/O that would otherwise be inaccessible to Python programmers, as well as other modules written in Python that provide standardized solutions for many problems that occur in everyday programming.

We will use the standard library extensively but we will first focus our attention on the language itself.

Just in case you get in your hands’ code written in the old Python 2.x at the end of this notebook you can see a quick summary of a few key differences between Python 2.x and 3.x

Example 2: The Barnsley fern

The Barnsley fern is a fractal named after the British mathematician Michael Barnsley who first described it in his book “Fractals Everywhere”. He made it to resemble the black spleenwort, Asplenium adiantum-nigrum. This fractal has served as inspiration to create natural structures using iterative mathematical functions.

Barnsley’s fern uses four affine transformation’s, i.e. simple vector transformations that include a vector-matrix multiplication and a translation. The formula for one transformation is the following:

[f_w(x,y) = \begin{bmatrix}a & b \ c & d \end{bmatrix} \begin{bmatrix} x \ y \end{bmatrix} + \begin{bmatrix} e \ f \end{bmatrix}]

Barnsley uses four transformations with weights for them to reproduce the fern leaf. The transformations are shown below.

[\begin{align} f_1(x,y) &= \begin{bmatrix} 0.00 & 0.00 \ 0.00 & 0.16 \end{bmatrix} \begin{bmatrix} x \ y \end{bmatrix} \[6px] f_2(x,y) &= \begin{bmatrix} 0.85 & 0.04 \ -0.04 & 0.85 \end{bmatrix} \begin{bmatrix} x \ y \end{bmatrix} + \begin{bmatrix} 0.00 \ 1.60 \end{bmatrix} \[6px] f_3(x,y) &= \begin{bmatrix} 0.20 & -0.26 \ 0.23 & 0.22 \end{bmatrix} \begin{bmatrix} x \ y \end{bmatrix} + \begin{bmatrix} 0.00 \ 1.60 \end{bmatrix} \[6px] f_4(x,y) &= \begin{bmatrix} -0.15 & 0.28 \ 0.26 & 0.24 \end{bmatrix} \begin{bmatrix} x \ y \end{bmatrix} + \begin{bmatrix} 0.00 \ 0.44 \end{bmatrix} \end{align}]

The probability factor $p$ for the four transformations can be seen in the table below:

[\begin{align} p[f_1] &\rightarrow 0.01 \[6px] p[f_2] &\rightarrow 0.85 \[6px] p[f_3] &\rightarrow 0.07 \[6px] p[f_4] &\rightarrow 0.07 \end{align}]

The first point drawn is at the origin $(x,y)=(0,0)$ and then the new points are iteratively computed by randomly applying one of the four coordinate transformations $f_1 \cdots f_4$

We will develop this program in two stages. First, we will try to use numpy. The de facto package for dealing with numerical arrays in Python. As we already know how to write functions, lets start writing four functions for the the four transformations. In this case we can define $r$ as being the vector (x,y). This will help us defining the functions in a very compact expression.

import numpy as np
import matplotlib.pyplot as plt

def f1(r):
    a=np.array([[0,0],[0,0.16]])
    return np.dot(a,r)

def f2(r):
    a=np.array([[0.85,0.04],[-0.04, 0.85]])
    return np.dot(a,r)+np.array([0.0,1.6])

def f3(r):
    a=np.array([[0.20,-0.26],[0.23,0.22]])
    return np.dot(a,r)+np.array([0.0,1.6])

def f4(r):
    a=np.array([[-0.15, 0.28],[0.26,0.24]])
    return np.dot(a,r)+np.array([0.0,0.44])

These four functions will transform points in $r$ into new positions $r’$. We can now assemble the code to assigned the transformations according to the probability factors described above.

r0=np.array([0,0])

npoints=100000

points=np.zeros((npoints,2))

fig, ax = plt.subplots()
                
for i in range(npoints):
    rnd=np.random.rand()
    if rnd<=0.01:
        r1=f1(r0)
    elif rnd<=0.86:
        r1=f2(r0)
    elif rnd<=0.93:
        r1=f3(r0)
    else:
        r1=f4(r0)
    points[i]=r0
    r0=r1

ax.plot(points[:,0],points[:,1],',')                
ax.set_axis_off()
ax.set_aspect(0.5)
plt.show()

png

Python Syntax I: Variables

Let us start with something very simple and then we will focus on different useful packages

print("Hello Word")  # Here I am adding a comment on the same line
# Comments like these will not do anything

Hello Word

Variable types, names, and reserved words

var = 8                # Integer     
k = 23434235234        # Long integer (all integers in Python 3 are long integers).
pi = 3.1415926         # float (there are better ways of defining PI with numpy)
z = 1.5+0.5j           # Complex
hi = "Hello world"    # String
truth = True           # Boolean

# Assignation to an operation
radius=3.0
area=pi*radius**2

Variables can have any name but you can not use reserved language names as:

and	as	assert	break	class	continue	def
del	elif	else	except	False	finally	for
from	global	if	import	in	is	lambda
None	nonlocal	not	or	pass	print	raise
return	True	try	while	with	yield

Other rules for variable names:

Can not start with a number: (example 12var)
Can not include illegal characters such as % & + - =, etc
Names in upper-case are considered different than those in lower-case

Variables can receive values assigned in several ways:

x=y=z=2.5
print(x,y,z)

2.5 2.5 2.5

a,b,c=1,2,3
print(a,b,c)

1 2 3

a,b=b,a+b
print(a,b)

2 3

import sys
print(sys.version)

3.11.7 (main, Dec 24 2023, 07:47:18) [Clang 12.0.0 (clang-1200.0.32.29)]

Basic data types

Numbers

Integers and floats work as you would expect from other languages:

x = 3
print(x, type(x))

3 <class 'int'>

print(x + 1)   # Addition;
print(x - 1)   # Subtraction;
print(x * 2)   # Multiplication;
print(x ** 2)  # Exponentiation;

x += 1
print(x)  # Prints "4"
x *= 2
print(x)  # Prints "8"

4
8

y = 2.5
print(type(y)) # Prints "<type 'float'>"
print(y, y + 1, y * 2, y ** 2) # Prints "2.5 3.5 5.0 6.25"

<class 'float'>
2.5 3.5 5.0 6.25

Note that unlike many languages (C for example), Python does not recognize the unary increment (x++) or decrement (x--) operators.

Python also has built-in types for long integers and complex numbers; you can find all of the details in the Official Documentation for Numeric Types.

Basic Mathematical Operations

With Python we can do the following basic operations:

Addition (+), subtraction (-), multiplication (*) and división (/).

Other less common:

Exponentiation (**), integer division (//) o module (%).

Precedence of Operations

PEDMAS
- Parenthesis
- Exponents
- Division and Multiplication.
- Addition and Substraction
From left to right.

Let’s see some examples:

print((3-1)*2)
print(3-1 *2)
print(1/2*4)

4
1
2.0

Booleans

Python implements all of the usual operators for Boolean logic, but uses English words rather than symbols (&&, ||, etc.):

t, f = True, False
print(type(t)) # Prints "<type 'bool'>"

<class 'bool'>

answer = True
answer

True

Now let’s look at the operations:

print(t and f) # Logical AND;
print(t or f)  # Logical OR;
print(not t)   # Logical NOT;
print(t != f)  # Logical XOR;

False
True
False
True

a=10
b=20
print (a==b)
print (a!=b)

False
True

a=10
b=20
print (a>b)
print (a<b)
print (a>=b)
#print (a=>b) # Error de sintaxis
print (a<=b)

False
True
False
True

Strings

hello = 'hello'   # String literals can use single quotes
world = "world"   # or double quotes; it does not matter.
print(hello, len(hello))

hello 5

hw = hello + ' ' + world  # String concatenation
print(hw)  # prints "hello world"

hello world

hw12 = '%s %s %d' % (hello, world, 12)  # sprintf style string formatting
print(hw12)  # prints "hello world 12"

hello world 12

String objects have a bunch of useful methods; for example:

s = "Monty Python"
print(s.capitalize())  # Capitalize a string; prints "Monty python"
print(s.upper())       # Convert a string to uppercase; prints "MONTY PYTHON"
print(s.lower())       # Convert a string to lowercase; prints "monty python"
print('>|'+s.rjust(40)+'|<')    # Right-justify a string, padding with spaces
print('>|'+s.center(40)+'|<')   # Center a string, padding with spaces
print(s.replace('y', '(wye)'))  # Replace all instances of one substring with another;
                                # prints "Mont(wye) P(wye)thon"

print('>|'+'      Monty Python    '.strip()+'|<')  # Strip leading and trailing whitespace

Monty python
MONTY PYTHON
monty python
>|                            Monty Python|<
>|              Monty Python              |<
Mont(wye) P(wye)thon
>|Monty Python|<

We can see a more general picture on how to slice a string as

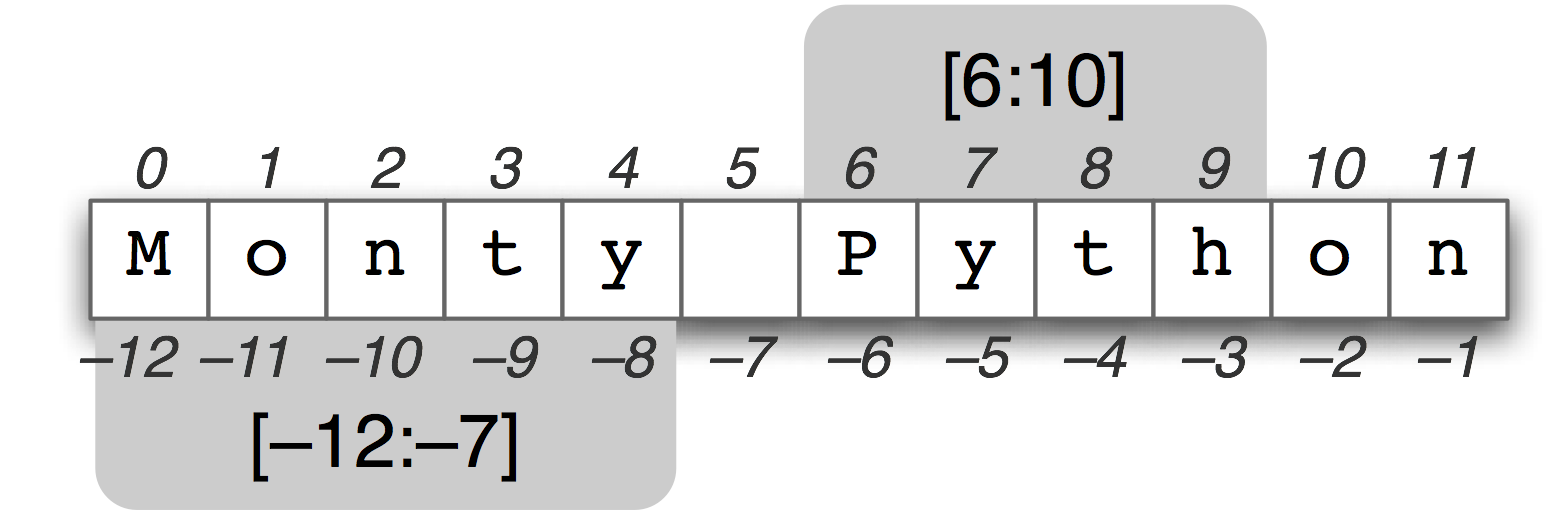
No fig directory

#  strings I

word = "Monty Python"
part = word[6:10]
print (part)
part = word[:4]
print(part)
part = word[5:]
print(part)
part = word[1:8:2] # from 1 to 8 in spaces of 2
print(part)
rev = word [::-1]
print(rev)
text = 'a,b,c'
text = text.split(',')
print(text)

c1="my.My.my.My"
c2="name"
c1+c2
c1*3
c1.split(".")

Pyth
Mont
 Python
ot y
nohtyP ytnoM
['a', 'b', 'c']

['my', 'My', 'my', 'My']

Today’s programs need to be able to handle a wide variety of characters. Applications are often internationalized to display messages and output in a variety of user-selectable languages; the same program might need to output an error message in English, French, Japanese, Hebrew, or Russian. Web content can be written in any of these languages and can also include a variety of emoji symbols. Python’s string type uses the Unicode Standard for representing characters, which lets Python programs work with all these different possible characters.

Unicode (https://www.unicode.org/) is a specification that aims to list every character used by human languages and give each character its unique code. The Unicode specifications are continually revised and updated to add new languages and symbols.

UTF-8 is one of the most commonly used encodings, and Python often defaults to using it.

You can find a list of all string methods in the Python 3.10 Language Documentation for Text sequence type (str).

String Formatting and text printing

In Python 3.x and higher, print() is a normal function as any other (so print(2, 3) prints “2 3”. If you see a code with a line like:

print 2, 3

This code is using Python 2.x syntax. This is just one of the backward incompatible differences introduced in Python 3.x. In Python 2.x and before print was a statement like if or for. In Python 3.x the statement was removed in favor of a function.

print("Hellow word!")
print()
print(7*3)

Hellow word!

21

name = "Theo"
print("His names is : ", name)
print()
grade = 19.5
neval = 3
print("Average : ", grade/neval),

# array 
a = [1, 2, 3, 4] 
  
# printing a element in same 
# line 
for i in range(4): 
    print(a[i], end =" ")  

His names is :  Theo

Average :  6.5
1 2 3 4 

There are four major ways to do string formatting in Python. These ways have evolved from the origin of the language itself trying to mimic the ways of other languages such as C or Fortran that have used certain formatting techniques for a long time.

Old style String Formatting (The `%` operator)

Strings in Python have a unique built-in operation that can be accessed with the % operator. This lets you do simple positional formatting very easily. This operator due its existence to the old printf-style function in C language. In C printf is a function that can receive several arguments. The string return is based on the first string and variables replaced with some special characters indicating the format of the variable should take as a string.

%s		string.
%d		integer.
%0xd		an integer with x zeros from the left.
%f		decimal notation with six digits.
%e		scientific notation (compact) with `e` in the exponent.
%E		scientific notation (compact) with `E` in the exponent.
%g		decimal or scientific notation with `e` in the exponent.
%G		decimal or scientific notation with `E` in the exponent.
%xz		format z adjusted to the rigth in a field of width x.
%-xz		format z adjusted to the left in a field of width x.
%.yz		format z with y digits.
%x.yz		format z with y digits in afield of width x .
%%		percentage sign.

See some examples of the use of this notation.

n = 15          # Int
r = 3.14159     # Float
s = "Hiii"      # String
print("|%4d, %6.4f|" % (n,r))                  
print("%e, %g" % (r,r))                          
print("|%2s, %4s, %5s, %10s|" % (s, s, s ,s))  

|  15, 3.1416|
3.141590e+00, 3.14159
|Hiii, Hiii,  Hiii,       Hiii|

'Hello, %s' % name

'Hello, Theo'

'The name %s has %d characters' % (name, len(name))

'The name Theo has 4 characters'

The new style String Formatting (str.format)

Python 3 introduced a new way to do string formatting. This “new style” string formatting gets rid of the %-operator special syntax and makes the syntax for string formatting more regular. Formatting is now handled by calling .format() on a string object.

You can use format() to do simple positional formatting, just like you could with “old style” formatting:

'Hello, {}'.format(name)

'Hello, Theo'

'The name {username} has {numchar} characters'.format(username=name, numchar= len(name))

'The name Theo has 4 characters'

In Python 3.x, this “new style” string formatting is to be preferred over %-style formatting. While “old style” formatting has been de-emphasized, it has not been deprecated. It is still supported in the latest versions of Python.

The even newer String Formatting style (Since Python 3.6)

Python 3.6 added a new string formatting approach called formatted string literals or “f-strings”. This new way of formatting strings lets you use embedded Python expressions inside string constants. Here’s a simple example to give you a feel for the feature:

f'The name {name} has {len(name)} characters'

'The name Theo has 4 characters'

Here we are not printing, just creating a string with replacements done on-the-fly indicated by the presence of the f'' before the string. You can do operations inside the string for example:

a = 2
b = 3
f'The sum of {a} and {b} is {a + b}, the product is {a*b} and the power {a}^{b} = {a**b}'

'The sum of 2 and 3 is 5, the product is 6 and the power 2^3 = 8'

Template Strings (Standard Library)

Here’s one more tool for string formatting in Python: template strings. It’s a simpler and less powerful mechanism, but in some cases, this might be exactly what you’re looking for.

from string import Template

t = Template('The name $name has $numchar characters')
t.substitute(name=name, numchar=len(name))

'The name Theo has 4 characters'

Python Syntax II: Sequence and Mapping Types. loops and conditionals

Python includes several built-in container types: lists, dictionaries, sets, and tuples. They are particularly useful when you are working with loops and conditionals. We will cover all these language elements here

Lists

The items of a list are arbitrary Python objects. Lists are formed by placing a comma-separated list of expressions in square brackets. (Note that there are no special cases needed to form lists of length 0 or 1.).

Lists are mutable meaning that they can be changed after they are created.

xs = [8, 4, 2]    # Create a list
print(xs, xs[2])
print(xs[-1])     # Negative indices count from the end of the list; prints "2"

[8, 4, 2] 2
2

xs[2] = 'cube'     # Lists can contain elements of different types
print(xs)

[8, 4, 'cube']

xs.append('tetrahedron')  # Add a new element to the end of the list
print(xs)  

[8, 4, 'cube', 'tetrahedron']

x = xs.pop()      # Remove and return the last element of the list
print(x, xs) 

tetrahedron [8, 4, 'cube']

words = ["triangle", ["square", "rectangle", "rhombus"], "pentagon"]
print(words[1][2])

rhombus

As usual, you can find all the more details about mutable in the Python 3.10 documentation for sequence types.

Slicing

In addition to accessing list elements one at a time, Python provides concise syntax to access sublists; this is known as slicing:

nums = range(5)      # range in Python 3.x is a built-in function that creates an iterable
lnums = list(nums)
print(lnums)         # Prints "[0, 1, 2, 3, 4]"
print(lnums[2:4])    # Get a slice from index 2 to 4 (excluding 4); prints "[2, 3]"
print(lnums[2:])     # Get a slice from index 2 to the end; prints "[2, 3, 4]"
print(lnums[:2])     # Get a slice from the start to index 2 (excluding 2); prints "[0, 1]"
print(lnums[:])      # Get a slice of the whole list; prints ["0, 1, 2, 3, 4]"
print(lnums[:-1])    # Slice indices can be negative; prints ["0, 1, 2, 3]"
lnums[2:4] = [8, 9] # Assign a new sublist to a slice
print(lnums)         # Prints "[0, 1, 8, 9, 4]"

[0, 1, 2, 3, 4]
[2, 3]
[2, 3, 4]
[0, 1]
[0, 1, 2, 3, 4]
[0, 1, 2, 3]
[0, 1, 8, 9, 4]

Loops over lists

You can loop over the elements of a list like this:

platonic=['Tetrahedron', 'Cube', 'Octahedron', 'Dodecahedron', 'Icosahedron']
for solid in platonic:
    print(solid)

Tetrahedron
Cube
Octahedron
Dodecahedron
Icosahedron

If you want access to the index of each element within the body of a loop, use the built-in enumerate function:

platonic=['Tetrahedron', 'Cube', 'Octahedron', 'Dodecahedron', 'Icosahedron']
for idx, solid in enumerate(platonic):
    print('#%d: %s' % (idx + 1, solid))

#1: Tetrahedron
#2: Cube
#3: Octahedron
#4: Dodecahedron
#5: Icosahedron

Copying lists:

# Assignment statements
# Incorrect copy

L=[]
M=L
 
# modify both lists
L.append('a')
print(L, M)

M.append('asd')
print(L,M)

['a'] ['a']
['a', 'asd'] ['a', 'asd']

#Shallow copy

L=[]
M=L[:]         # Shallow copy using slicing
N=list(L)      # Creating another shallow copy

# modify only one
L.append('a')
print(L, M, N)

['a'] [] []

Shallow copy vs Deep Copy

Assignment statements in Python do not copy objects, they create bindings between a target and an object. Therefore, the problem with shallow copies is that internal objects are only referenced

lst1 = ['a','b',['ab','ba']]
lst2 = lst1[:]

lst2[2][0]='cd'
print(lst1)

['a', 'b', ['cd', 'ba']]

lst1 = ['a','b',['ab','ba']]
lst2 = list(lst1)

lst2[2][0]='cd'
print(lst1)

['a', 'b', ['cd', 'ba']]

To produce a deep copy you can use a module from the Python Standard Library. The Python Standard library will be covered in the next Notebook, however, this is a good place to clarify this important topic about Shallow and Deep copies in Python.

from copy import deepcopy

lst1 = ['a','b',['ab','ba']]
lst2 = deepcopy(lst1)

lst2[2][0]='cd'
print(lst1)

['a', 'b', ['ab', 'ba']]

Deleting lists:

platonic=['Tetrahedron', 'Cube', 'Octahedron', 'Dodecahedron', 'Icosahedron']
print(platonic)
del platonic

try: platonic
except NameError: print("The variable 'platonic' is not defined")

['Tetrahedron', 'Cube', 'Octahedron', 'Dodecahedron', 'Icosahedron']
The variable 'platonic' is not defined

platonic=['Tetrahedron', 'Cube', 'Octahedron', 'Dodecahedron', 'Icosahedron']
del platonic[1]
print(platonic)
del platonic[-1]                  #Delete last element 
print(platonic)

platonic=['Tetrahedron', 'Cube', 'Octahedron', 'Dodecahedron', 'Icosahedron']
platonic.remove("Cube")
print(platonic)

newl=["Circle", 2]
print(platonic+newl) 
print(newl*2)
print(2*newl)

['Tetrahedron', 'Octahedron', 'Dodecahedron', 'Icosahedron']
['Tetrahedron', 'Octahedron', 'Dodecahedron']
['Tetrahedron', 'Octahedron', 'Dodecahedron', 'Icosahedron']
['Tetrahedron', 'Octahedron', 'Dodecahedron', 'Icosahedron', 'Circle', 2]
['Circle', 2, 'Circle', 2]
['Circle', 2, 'Circle', 2]

Sorting lists:

list1=['Tetrahedron', 'Cube', 'Octahedron', 'Dodecahedron', 'Icosahedron']
list2=[1,200,3,10,2,999,-1]
list1.sort()
list2.sort()
print(list1)
print(list2)

['Cube', 'Dodecahedron', 'Icosahedron', 'Octahedron', 'Tetrahedron']
[-1, 1, 2, 3, 10, 200, 999]

List comprehensions:

When programming, frequently we want to transform one type of data into another. As a simple example, consider the following code that computes square numbers:

nums = [0, 1, 2, 3, 4]
squares = []
for x in nums:
    squares.append(x ** 2)
print(squares)

[0, 1, 4, 9, 16]

You can make this code simpler using a list comprehension:

nums = [0, 1, 2, 3, 4]
squares = [x ** 2 for x in nums]
print(squares)

[0, 1, 4, 9, 16]

List comprehensions can also contain conditions:

nums = [0, 1, 2, 3, 4]
even_squares = [x ** 2 for x in nums if x % 2 == 0]
print(even_squares)

[0, 4, 16]

Dictionaries

A dictionary stores (key, value) pairs, similar to a Map in Java or an object in Javascript. You can use it like this:

# Create a new dictionary with some data about regular polyhedra
rp = {'Tetrahedron': 4, 'Cube': 6, 'Octahedron': 8, 'Dodecahedron': 12, 'Icosahedron': 20}  
print(rp['Cube'])              # Get an entry from a dictionary; prints "cute"
print('Icosahedron' in rp)     # Check if a dictionary has a given key; prints "True"

6
True

rp['Circle'] = 0         # Set an entry in a dictionary
print(rp['Circle'])      # Prints "0"

'Heptahedron' in rp

False

print(rp.get('Hexahedron', 'N/A'))  # Get an element with a default; prints "N/A"
print(rp.get('Cube', 'N/A'))        # Get an element with a default; prints 6

N/A
6

del rp['Circle']        # Remove an element from a dictionary
print(rp.get('Circle', 'N/A')) # "Circle" is no longer a key; prints "N/A"

N/A

You can find all you need to know about dictionaries in the Python 3.10 documentation for Mapping types.

It is easy to iterate over the keys in a dictionary:

rp = {'Tetrahedron': 4, 'Cube': 6, 'Octahedron': 8, 'Dodecahedron': 12, 'Icosahedron': 20}  
for polyhedron in rp:
    faces = rp[polyhedron]
    print('The %s has %d faces' % (polyhedron.lower(), faces))

for n in rp.keys():
    print(n,rp[n])

The tetrahedron has 4 faces
The cube has 6 faces
The octahedron has 8 faces
The dodecahedron has 12 faces
The icosahedron has 20 faces
Tetrahedron 4
Cube 6
Octahedron 8
Dodecahedron 12
Icosahedron 20

If you want access to keys and their corresponding values, use the items() method. This is an iterable, not a list.

rp = {'Tetrahedron': 4, 'Cube': 6, 'Octahedron': 8, 'Dodecahedron': 12, 'Icosahedron': 20}  
for polyhedron, faces in rp.items():
    print('The %s has %d faces' % (polyhedron, faces))

The Tetrahedron has 4 faces
The Cube has 6 faces
The Octahedron has 8 faces
The Dodecahedron has 12 faces
The Icosahedron has 20 faces

Dictionary comprehensions: These are similar to list comprehensions, but allow you to easily construct dictionaries. For example:

nums = [0, 1, 2, 3, 4]
even_num_to_square = {x: x ** 2 for x in nums if x % 2 == 0}
print(even_num_to_square)

{0: 0, 2: 4, 4: 16}

Sets

A set is an unordered collection of distinct elements. As a simple example, consider the following:

polyhedron = {'tetrahedron', 'hexahedron', 'icosahedron'}
print('tetrahedron' in polyhedron)   # Check if an element is in a set; prints "True"
print('sphere' in polyhedron)    # prints "False"

True
False

polyhedron.add('cube')        # Add an element to a set
print('cube' in polyhedron)
print(len(polyhedron))       # Number of elements in a set;

True
4

polyhedron.add('hexahedron')   # Adding an element that is already in the set does nothing
print(polyhedron)       
polyhedron.remove('cube')      # Remove an element from a set
print(polyhedron)       

{'hexahedron', 'cube', 'tetrahedron', 'icosahedron'}
{'hexahedron', 'tetrahedron', 'icosahedron'}

setA = set(["first", "second", "third", "first"])
print("SetA = ",setA)
setB = set(["second", "fourth"])
print("SetB=",setB)

print(setA & setB)                       # Intersection
print(setA | setB)                       # Union
print(setA - setB)                       # Difference A-B
print(setB - setA)                       # Difference B-A
print(setA ^ setB)                       # symmetric difference
set(['fourth', 'first', 'third'])

# Set is not mutable, elements of the frozen set remain the same after creation
immutable_set = frozenset(["a", "b", "a"])   
print(immutable_set)

SetA =  {'third', 'first', 'second'}
SetB= {'fourth', 'second'}
{'second'}
{'third', 'first', 'second', 'fourth'}
{'third', 'first'}
{'fourth'}
{'fourth', 'third', 'first'}
frozenset({'a', 'b'})

Loops over sets

Iterating over a set has the same syntax as iterating over a list; however since sets are unordered, you cannot make assumptions about the order in which you visit the elements of the set:

animals = {'cat', 'dog', 'fish'}
for idx, animal in enumerate(animals):
    print('#%d: %s' % (idx + 1, animal))
# Prints "#1: fish", "#2: dog", "#3: cat"

#1: dog
#2: cat
#3: fish

Set comprehensions: Like lists and dictionaries, we can easily construct sets using set comprehensions:

from math import sqrt
lc=[int(sqrt(x)) for x in range(30)]
sc={int(sqrt(x)) for x in range(30)}

print(lc)
print(sc)

[0, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5]
{0, 1, 2, 3, 4, 5}

set(lc)

{0, 1, 2, 3, 4, 5}

Tuples

A tuple is an (immutable) ordered list of values. A tuple is in many ways similar to a list; one of the most important differences is that tuples can be used as keys in dictionaries and as elements of sets, while lists cannot.

Some general observations on tuples are:

1) A tuple can not be modified after its creation.

2) A tuple is defined similarly to a list, only that the set is enclosed with parenthesis, “()”, instead of “[]”.

3) The elements in the tuple have a predefined order, similar to a list.

4) Tuples have the first index as zero, similar to lists, such that t[0] always exist.

5) Negative indices count from the end, as in lists.

6) Slicing works as in lists.

7) Extracting sections of a list gives a list, similarly, a section of a tuple, gives a tuple.

8) append or sort do not work in tuples. “in” can be used to know if an element exists in a tuple.

9) Tuples are much faster than lists.

10) If you are defining a fixed set of values and the only thing you would do is to run over it, use a tuple instead of a list.

11) Tuples can be converted in lists list(tuple) and lists in tuples tuple(list)

d = {(x, x + 1): x for x in range(10)}  # Create a dictionary with tuple keys
t = (5, 6)       # Create a tuple
print(type(t))
print(d[t])       
print(d[(1, 2)])
print(d)
e = (1,2,'a','b')
print(type(e))
#print('MIN of Tuple=',min(e))

e = (1,2,3,4)
print('MIN of Tuple=',min(e))

word = 'abc'
L = list(word)
lp=list(word)
tp=tuple(word)
print(lp,tp)

<class 'tuple'>
5
1
{(0, 1): 0, (1, 2): 1, (2, 3): 2, (3, 4): 3, (4, 5): 4, (5, 6): 5, (6, 7): 6, (7, 8): 7, (8, 9): 8, (9, 10): 9}
<class 'tuple'>
MIN of Tuple= 1
['a', 'b', 'c'] ('a', 'b', 'c')

#TypeError: 'tuple' object does not support item assignment

#t[0] = 1  

Conditionals

Conditionals are expressions that can be true or false. For example
- have the user type the correct word?
- is the number bigger than 100?
The result of the conditions will decide what will happen, for example:
- When the input word is correct, print “Good”
- To all numbers larger than 100 subtract 20.

Boolean Operators

x = 125
y = 251

print(x == y)    # x equal to y
print(x != y)    # x is not equal to y
print(x >  y)    # x is larger than y
print(x <  y)    # x is smaller than y
print(x >= y)    # x is larger or equal than y
print(x <= y)    # x is smaller or equal than y
print(x == 125)  # x is equal to 125

False
True
False
True
False
True
True

passwd = "nix"
num  = 10
num1 = 20
letter = "a"

print(passwd == "nix")
print(num >= 0)
print(letter > "L")
print(num/2 == (num1-num))
print(num %5 != 0)

True
True
True
False
False

s1="A"
s2="Z"

print(s1>s2)
print(s1.isupper())
print(s1.lower()>s2)

False
True
True

Conditional (if…elif…else)

# Example with the instruction if
platonic = {4: "tetrahedron", 
            6: "hexahedron",
            8: "octahedron",
            12: "dodecahedron",
            20: "icosahedron"}

num_faces = 6

if num_faces in platonic.keys():
    print(f"There is a regular solid with {num_faces} faces and the name is {platonic[num_faces]}")  
else:
    print(f"Theres is no regular polyhedron with {num_faces} faces")
    
#The of the compact form of  if...else

evenless = "Polyhedron exists" if (num_faces in platonic.keys()) else "Polyhedron does not exist"
print(evenless)

There is a regular solid with 6 faces and the name is hexahedron
Polyhedron exists

# Example of if...elif...else
x=-10
    
if x<0 :
    print(x," is negative")
elif x==0 :
    print("the number is zero")
else:
    print(x," is positive")

-10  is negative

# example of the keyword pass

if x<0:
   print("x is negative")
else:
   pass # I will not do anything 

x is negative

Loop with conditional (while)

# Example with while

x=0
while x < 10:
     print(x)
     x = x+1
print("End")

# A printed table with tabular with while

x=1

while x < 10:
     print(x, "\t", x*x)
     x = x+1

# Comparing while and for in a string
word = "program of nothing"
index=0
while index < len(word):
    print(word[index], end ="") 
    index +=1
print()
for letter in word:
      print(letter,end="")

program of nothing
program of nothing

#Using enumerate for lists

colors=["red", "green", "blue"]
for c in colors:    
    print(c,end=" ")
print() 
for i, col in enumerate(colors):
    print(i,col) 

red green blue 
red
green
blue

#Running over several lists at the same time

colors1 =["rojo","verde", "azul"]
colors2 =["red", "green", "blue"]
for ce, ci in zip(colors1,colors2):    
    print("Color",ce,"in Spanish means",ci,"in english")

Color rojo in Spanish means red in english
Color verde in Spanish means green in english
Color azul in Spanish means blue in english

List of numbers (range)

print(list(range(10)))
print(list(range(2,10)))
print(list(range(0,11,2)))

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[2, 3, 4, 5, 6, 7, 8, 9]
[0, 2, 4, 6, 8, 10]

A simple application of the function range() is when we try to calculate finite sums of integers. For example

\begin{equation} \boxed{ \sum_{i=1}^n i = \frac{n(n+1)}2\ , \ \ \ \ \ \sum_{i=1}^n i^2 = \frac{n(n+1)(2n+1)}6\ . } \end{equation}

n = 100
    
sum_i=0
sum_ii=0
for i in range(1,n+1):
     sum_i = sum_i + i
     sum_ii += i*i
print(sum_i, n*(n+1)/2) 
print(sum_ii, n*(n+1)*(2*n+1)/6)

5050 5050.0
338350 338350.0

Loop modifiers: break and continue

for n in range(1,10):
      c=n*n
      if c > 50:
            print(n, "to the square is ",c," > 50")
            print("STOP")
            break
      else:
            print(n," with square ",c)

for i in range(-5,5,1):
    if i == 0:
        continue
    else:
        print(round(1/i,3))

1  with square  1
2  with square  4
3  with square  9
4  with square  16
5  with square  25
6  with square  36
7  with square  49
8 to the square is  64  > 50
STOP
-0.2
-0.25
-0.333
-0.5
-1.0
1.0
0.5
0.333
0.25

Python Syntax III: Functions

A function defines a set of instructions or a piece of a code with an associated name that performs a specific task and it can be re-utilized.

It can have an argument(s) or not, it can return values or not.

The functions can be given by the language, imported from an external file (module), or created by you

Example 3: Julia Sets

"""
Solution from:
https://codereview.stackexchange.com/questions/210271/generating-julia-set
"""
from functools import partial
from numbers import Complex
from typing import Callable

import matplotlib.pyplot as plt
import numpy as np


def douady_hubbard_polynomial(z: Complex,
                              c: Complex) -> Complex:
    """
    Monic and centered quadratic complex polynomial
    https://en.wikipedia.org/wiki/Complex_quadratic_polynomial#Map
    """
    return z ** 2 + c


def julia_set(mapping: Callable[[Complex], Complex],
              *,
              min_coordinate: Complex,
              max_coordinate: Complex,
              width: int,
              height: int,
              iterations_count: int = 256,
              threshold: float = 2.) -> np.ndarray:
    """
    As described in https://en.wikipedia.org/wiki/Julia_set
    :param mapping: function defining Julia set
    :param min_coordinate: bottom-left complex plane coordinate
    :param max_coordinate: upper-right complex plane coordinate
    :param height: pixels in vertical axis
    :param width: pixels in horizontal axis
    :param iterations_count: number of iterations
    :param threshold: if the magnitude of z becomes greater
    than the threshold we assume that it will diverge to infinity
    :return: 2D pixels array of intensities
    """
    im, re = np.ogrid[min_coordinate.imag: max_coordinate.imag: height * 1j,
                      min_coordinate.real: max_coordinate.real: width * 1j]
    z = (re + 1j * im).flatten()

    live, = np.indices(z.shape)  # indexes of pixels that have not escaped
    iterations = np.empty_like(z, dtype=int)

    for i in range(iterations_count):
        z_live = z[live] = mapping(z[live])
        escaped = abs(z_live) > threshold
        iterations[live[escaped]] = i
        live = live[~escaped]
        if live.size == 0:
            break
    else:
        iterations[live] = iterations_count

    return iterations.reshape((height, width))

mapping = partial(douady_hubbard_polynomial,
                  c=-0.7 + 0.27015j)  # type: Callable[[Complex], Complex]

image = julia_set(mapping,
                  min_coordinate=-1.5 - 1j,
                  max_coordinate=1.5 + 1j,
                  width=800,
                  height=600)
plt.axis('off')
plt.imshow(image,
           cmap='nipy_spectral_r',
           origin='lower')
plt.savefig("julia_python.png")
plt.show()

png

Example 4: Mandelbrot Set

import matplotlib.pyplot as plt
from pylab import arange, zeros, xlabel, ylabel
from numpy import NaN

def m(a):
    z = 0
    for n in range(1, 100):
        z = z**2 + a
        if abs(z) > 2:
            return n
    return NaN

X = arange(-2, .5, .002)
Y = arange(-1,  1, .002)
Z = zeros((len(Y), len(X)))

for iy, y in enumerate(Y):
    #print (iy, "of", len(Y))
    for ix, x in enumerate(X):
        Z[iy,ix] = m(x + 1j * y)

plt.imshow(Z, cmap = plt.cm.prism_r, interpolation = 'none', extent = (X.min(), X.max(), Y.min(), Y.max()))
xlabel("Re(c)")
ylabel("Im(c)")
plt.axis('off')
plt.savefig("mandelbrot_python.png")
plt.show()

png

Some Built-in functions

To see which functions are available in python, go to the web site Python 3.10 Documentation for Built-in Functions

float(obj): convert a string or a number (integer or long integer) into a float number.

int(obj): convert a string or a number (integer or long integer) into an integer.

str(num): convert a number into a string.

divmod(x,y): return the results from x/y y x%y.

pow(x,y): return x to the power y.

range(start,stop,step): return a list of number from start to stop-1 in steps.

round(x,n): return a float value x rounding to n digits after the decimal point. If n is omitted, the value per default is zero.

len(obj): return the len of string, lista, tupla o diccionary.

Modules from Python Standard Library

We will see more about these functions on the next notebook We will show here just a few from the math module

import math

math.sqrt(2)

1.4142135623730951

math.log10(10000)

4.0

math.hypot(3,4)

5.0

Back in the 90’s many scientific handheld calculators could not compute factorials beyond $69!$. Let’s see in Python:

math.factorial(70)

11978571669969891796072783721689098736458938142546425857555362864628009582789845319680000000000000000

float(math.factorial(70))

1.1978571669969892e+100

import calendar

calendar.prcal(2024)
calendar.prmonth(2024, 7)

                                  2024

      January                   February                   March
Mo Tu We Th Fr Sa Su      Mo Tu We Th Fr Sa Su      Mo Tu We Th Fr Sa Su
 1  2  3  4  5  6  7                1  2  3  4                   1  2  3
 8  9 10 11 12 13 14       5  6  7  8  9 10 11       4  5  6  7  8  9 10
15 16 17 18 19 20 21      12 13 14 15 16 17 18      11 12 13 14 15 16 17
22 23 24 25 26 27 28      19 20 21 22 23 24 25      18 19 20 21 22 23 24
29 30 31                  26 27 28 29               25 26 27 28 29 30 31

       April                      May                       June
Mo Tu We Th Fr Sa Su      Mo Tu We Th Fr Sa Su      Mo Tu We Th Fr Sa Su
 1  2  3  4  5  6  7             1  2  3  4  5                      1  2
 8  9 10 11 12 13 14       6  7  8  9 10 11 12       3  4  5  6  7  8  9
15 16 17 18 19 20 21      13 14 15 16 17 18 19      10 11 12 13 14 15 16
22 23 24 25 26 27 28      20 21 22 23 24 25 26      17 18 19 20 21 22 23
29 30                     27 28 29 30 31            24 25 26 27 28 29 30

        July                     August                  September
Mo Tu We Th Fr Sa Su      Mo Tu We Th Fr Sa Su      Mo Tu We Th Fr Sa Su
 1  2  3  4  5  6  7                1  2  3  4                         1
 8  9 10 11 12 13 14       5  6  7  8  9 10 11       2  3  4  5  6  7  8
15 16 17 18 19 20 21      12 13 14 15 16 17 18       9 10 11 12 13 14 15
22 23 24 25 26 27 28      19 20 21 22 23 24 25      16 17 18 19 20 21 22
29 30 31                  26 27 28 29 30 31         23 24 25 26 27 28 29
                                                    30

      October                   November                  December
Mo Tu We Th Fr Sa Su      Mo Tu We Th Fr Sa Su      Mo Tu We Th Fr Sa Su
    1  2  3  4  5  6                   1  2  3                         1
 7  8  9 10 11 12 13       4  5  6  7  8  9 10       2  3  4  5  6  7  8
14 15 16 17 18 19 20      11 12 13 14 15 16 17       9 10 11 12 13 14 15
21 22 23 24 25 26 27      18 19 20 21 22 23 24      16 17 18 19 20 21 22
28 29 30 31               25 26 27 28 29 30         23 24 25 26 27 28 29
                                                    30 31
     July 2024
Mo Tu We Th Fr Sa Su
 1  2  3  4  5  6  7
 8  9 10 11 12 13 14
15 16 17 18 19 20 21
22 23 24 25 26 27 28
29 30 31

Functions from external modules

These functions come from modules. The way to do so is by doing

import module_name

Once it is imported, we can use the functions contained in this module by using

module_name.existing_funtion(expected_input_variables)

some module names can be long or complicated. you can then use

import module_name as mn

and then to use it, you say

mn.existing_funtion(expected_input_variables)

if you want to import only a few functions from the module, you can say

from stuff import f, g
print f("a"), g(1,2)

You can also import all function as

from stuff import *
print f("a"), g(1,2)

Combining with the nickname for the module, we can say

from stuff import f as F
from stuff import g as G
print F("a"), G(1,2)

import math

def myroot(num):
    if num<0:
         print("Enter a positive number")
         return
    print(math.sqrt(num))

# main
myroot(9)
myroot(-8)
myroot(2)

3.0
Enter a positive number
1.4142135623730951

def addthem(x,y):
   return x+y

# main
add = addthem(5,6) # Calling the function
print(add)

We can declare functions with optional parameters. NOTE: The optional parameters NEED to be always at the end

def operations(x,y,z=None):
    if (z==None):
        sum = x+y
        rest = x-y
        prod= x*y
        div = x/y 
    else:
        sum = z+x+y
        rest = x-y-z
        prod= x*y*z
        div = x/y/z 
    return sum,rest,prod,div

# main
print(operations(5,6))
a,b,c,d = operations(8,4)
print(a,b,c,d)
a,b,c,d = operations(8,4,5)
print(a,b,c,d)

(11, -1, 30, 0.8333333333333334)
12 4 32 2.0
17 -1 160 0.4

We can even pass a function to a variable and we can pass this to other function (this is called functional programming)

def operations(x,y,z=None,flag=False):
    if (flag == True):
        print("Flag is true")
    if (z==None):
        sum = x+y
        rest = x-y
        prod= x*y
        div = x/y 
    else:
        sum = z+x+y
        rest = x-y-z
        prod= x*y*z
        div = x/y/z 
    return sum,rest,prod,div
print(operations(5,6,flag=True))

Flag is true
(11, -1, 30, 0.8333333333333334)

Example 5: Fibonacci Sequences and Golden Ratio

At this point, you have seen enough material to start doing some initial scientific computing. Let’s start applying all that you have learned up to now.

For this introduction to Python language, we will use the Fibonacci Sequence as an excuse to start using the basics of the language.

The Fibonacci sequence is a series of numbers generated iteratively like this

$F_n=F_{n-1}+F_{n-2}$

where we can start with seeds $F_0=0$ and $F_1=1$

Starting with those seeds we can compute $F_2$, $F_3$ and so on until an arbitrary large $F_n$

The Fibonacci Sequence looks like this:

[0,\; 1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\;]

Let’s play with this in our first Python program.

Let’s start by defining the first two elements in the Fibonacci series

a = 0
b = 1

We now know that we can get a new variable to store the sum of a and b

c = a + b

Remember that the built-in function range() generates the immutable sequence of numbers starting from the given start integer to the stop integer.

range(10)

range(0, 10)

The range() function doesn’t generate all numbers at once. It produces numbers one by one as the loop moves to the next number. So it consumes less memory and resources. You can get the list consuming all the values from the sequence.

list(range(10))

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

Now we can introduce a for using the iterable range(10) loop to see the first 10 elements in the Fibonacci sequence

a = 0
b = 1
print(a)
print(b)
for i in range(10):
    c = a+b
    print(c)
    a = b
    b = c

This is a simple way to iteratively generate the Fibonacci sequence. Now, imagine that we want to store the values of the sequence. Lists are the best containers so far, there are better options with Numpy something that we will see later. We can just use the append method for the list and continuously add new numbers to the list.

fib = [0, 1]
for i in range(1,11):
    fib.append(fib[i]+fib[i-1])
print(fib)

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89]

The append method works by adding the element at the end of the list.

Let’s continue with the creation of a Fibonacci function. We can create a Fibonacci function to return the Fibonacci number for an arbitrary iteration, see for example:

def fibonacci_recursive(n):
    if n < 2:
        return n
    else:
        return fibonacci_recursive(n-2) + fibonacci_recursive(n-1)

fibonacci_recursive(6)

We can recreate the list using this function, see the next code:

print([ fibonacci_recursive(n) for n in range (20) ])

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181]

We are using a list comprehension. There is another way to obtain the same result using the so-called lambda functions:

print(list(map(lambda x: fibonacci_recursive(x), range(20))))

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181]

lambda functions are some sort of anonymous functions. They are indeed very popular in functional programming and Python with its multiparadigm style makes lambda functions commonplace in many situations.

Using fibonacci_recursive is very inefficient of generate the Fibonacci sequence even more as n increases. The larger the value of n more calls to fibonacci_recursive is necessary.

There is an elegant solution to use the redundant recursion:

def fibonacci_fastrec(n):
    def fib(prvprv, prv, c):
        if c < 1: return prvprv
        else: return fib(prv, prvprv + prv, c - 1) 
    return fib(0, 1, n)

print([ fibonacci_fastrec(n) for n in range (20) ])

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181]

This solution is still recursive but avoids the two-fold recursion from the first function. With IPython we can use the magic %timeit to benchmark the difference between both implementations

%timeit [fibonacci_fastrec(n) for n in range (20)]

25.6 µs ± 625 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each)

%timeit [fibonacci_recursive(n) for n in range (20)]

2.18 ms ± 40.8 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

%timeit is not a Python command. It is a magic command of IPython, however, Python itself provides a more restrictive functionality. This can be provided with the time package:

import time

start = time.time()
print("hello")
end = time.time()
print(end - start)

hello
0.00046062469482421875

Finally, there is also an analytical expression for the Fibonacci sequence, so the entire recursion could be avoided.

from math import sqrt
 
def analytic_fibonacci(n):
    if n == 0:
        return 0
    else:
        sqrt_5 = sqrt(5);
        p = (1 + sqrt_5) / 2;
        q = 1/p;
        return int( (p**n + q**n) / sqrt_5 + 0.5 )
 

print([ analytic_fibonacci(n) for n in range (40) ])

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986]

%timeit [analytic_fibonacci(n) for n in range (40)]

20.8 µs ± 3.15 µs per loop (mean ± std. dev. of 7 runs, 100,000 loops each)

There is an interesting property of the Fibonacci sequence, the ratio between consecutive elements converges to a finite value, the so-called golden number. Let us store this ratio number in a list as the Fibonacci series grow. Here we introduce the function zip() from Python. zip() is used to map the similar index of multiple containers so that they can be used just using as a single entity. As zip is not easy to understand and before we describe the Fibonacci method, let me give you a simple example of using zip

# initializing lists 
sentence = [ "I", "am", "the Fibonacci", "Series" ] 
first_serie = [ 1, 1, 2, 3 ] 
second_serie = [ 144, 233, 377, 610 ] 
  
mapped = zip(sentence, first_serie,second_serie) 
  
# converting values to print as set 
mapped = set(mapped) 
   
print ("The zipped result is : ",end="") 
print (mapped) 

# Unzipping means converting the zipped values back to the individual self as they were. 
# This is done with the help of “*” operator.

s1, s2, s3 = zip(*mapped) 

print ("First string : ",end="") 
print (s1) 
  
print ("Second string : ",end="") 
print (s2) 
  
print ("Third string : ",end="") 
print (s3) 

The zipped result is : {('the Fibonacci', 2, 377), ('I', 1, 144), ('Series', 3, 610), ('am', 1, 233)}
First string : ('the Fibonacci', 'I', 'Series', 'am')
Second string : (2, 1, 3, 1)
Third string : (377, 144, 610, 233)

Now let us go back to Fibonacci

fib= [fibonacci_fastrec(n) for n in range (40)]
X=[ x/y for x,y in zip(fib[2:],fib[1:-1]) ]
X

[1.0,
0,
5,
6666666666666667,
6,
625,
6153846153846154,
619047619047619,
6176470588235294,
6181818181818182,
6179775280898876,
6180555555555556,
6180257510729614,
6180371352785146,
618032786885246,
618034447821682,
6180338134001253,
618034055727554,
6180339631667064,
6180339985218033,
618033985017358,
6180339901755971,
618033988205325,
618033988957902,
6180339886704431,
6180339887802426,
618033988738303,
6180339887543225,
6180339887482036,
6180339887505408,
6180339887496482,
618033988749989,
618033988749859,
6180339887499087,
6180339887498896,
618033988749897,
618033988749894,
6180339887498951]

The asymptotic value of the ratio is called the Golden Ratio, its value is $\varphi = \frac{1+\sqrt{5}}{2} = 1.6180339887\ldots.$

import math

golden=(1+math.sqrt(5))/2

We can now plot how each ratio in the Fibonacci sequence is closer and closer to the golden ratio

import matplotlib.pyplot as plt

plt.semilogy([math.fabs(x - golden) for x in X]);

png

Functional Programming

Before we discuss object-oriented programming, it will be useful to discuss functional programming. This is the ability in python that a function can be called by another function.

The benefit of functional programming is to make your program less error-prone. Functional programming is more predictable and easier to see the outcome. Many scientific libraries adopt a functional programming paradigm.

There are several existing cases in python.

#map() function
import numpy as np

a=np.random.rand(20)
b=np.random.rand(20)

#here min is an existing function that compares two arguments, we can even create a function and use it in map
lower=map(min,a,b)
# this is an example of lazy evaluation, this is now an object, we will see the result only when we ask for the
# result.
print(lower)
#now let us see what is inside
print(list(lower))

<map object at 0x1387e9450>
[0.3479198420638585, 0.5885103951618519, 0.09788507744404285, 0.3973200826407489, 0.07151476024779557, 0.19961585086696665, 0.018736801582169504, 0.47433177615457234, 0.09502722987767931, 0.7955147481783459, 0.2968562440518463, 0.25457189637169564, 0.2402732992180341, 0.19322876498279506, 0.15700028427906199, 0.2786921343509716, 0.2323972417087179, 0.8323196759092788, 0.14846718946296644, 0.7057084437708713]

#lambda this is a method to define a function in a single line
#in this example we define a function that received three parameters and sums them up.
myfunction=lambda a,b,c: a+b+c
print(myfunction(1,2,3))

#another example
a=["phone:333333","email:al@gmail.com"]
for a in a:
    print((lambda x: x.split(":")[0] + ' ' + x.split(":")[-1])(a))

6
phone 333333
email al@gmail.com

Python Syntax IV: Object-Oriented Programming

Object-oriented programming (OOP) is a programming paradigm based on the concept of objects, which can contain data, in the form of fields (often known as attributes or properties), and code, in the form of procedures (often known as methods). A feature of objects is an object’s procedure that can access and often modify the data fields of the object with which they are associated (objects have a notion of “this” or “ self”). In OOP, computer programs are designed by making them out of objects that interact with one another.

Object-oriented programming is more than just classes and objects; it’s a whole programming paradigm based around [sic] objects (data structures) that contain data fields and methods. It is essential to understand this; using classes to organize a bunch of unrelated methods together is not object orientation.

Junade Ali, Mastering PHP Design Patterns

Class is a central concept in OOP. Classes provide means of bundling data and functionality together. Instances of a class are called objects. Each class instance can have attributes attached to it for maintaining its state. Class instances can also have methods (defined by their class) for modifying their state.

The syntax for defining classes in Python is shown with some plain examples. Anything indented in the class is within the scope of the class. Usually, they are named such that the first letter is capitalized. Variables can be defined within the class but you can also initialize some variables by calling, init, which sets the values for any parameters that need to be defined when an object is first created. You define the methods within the class but to have access to that method, you need to include self in the method signature. Now, to use, you just call the class, which then will create all variables within the class. If the class is created with some parameter, it will pass directly the variable that has been instantiated in init.

class Greeter:
    myvariable='nothing of use'


    # Constructor
    def __init__(self, name):
        self.name = name  # Create an instance variable

    # Instance method
    def greet(self, loud=False):
        if loud:
            print('HELLO, %s!' % self.name.upper())
        else:
            print('Hello, %s' % self.name)

g = Greeter('Fred')  # Construct an instance of the Greeter class
g.greet()            # Call an instance method; prints "Hello, Fred"
g.greet(loud=True)   # Call an instance method; prints "HELLO, FRED!"

Hello, Fred
HELLO, FRED!

# Let us start with a very simple class

class MyClass:
#create objects with instances customized to a specific initial state, here data is defined as an empty vector
#The self parameter is a reference to the current instance of the class, 
#and is used to access variables that belong to the class
    def __init__(self):
        self.data = []
    """A simple example class"""
    i = 12345

    def f(self):
        return 'hello world'

#instantiation the class
x=MyClass
print(x.i)
print(x.f)

12345
<function MyClass.f at 0x1388a5d00>

class Person:
  def __init__(self, name, age):
    self.name = name
    self.age = age

  def myfunc(self):
    print("Hello my name is " + self.name)

p1 = Person("John", 36)


print(p1.name)
print(p1.age)
p1.myfunc()
     

John
36
Hello my name is John

class Rocket():
    # Rocket simulates a rocket ship for a game,
    #  or a physics simulation.
    
    def __init__(self):
        # Each rocket has an (x,y) position.
        self.x = 0
        self.y = 0
        
    def move_up(self):
        # Increment the y-position of the rocket.
        self.y += 1
        
# Create a fleet of 5 rockets and store them in a list.
my_rockets = [Rocket() for x in range(0,5)]

# Move the first rocket up.
my_rockets[0].move_up()

# Show that only the first rocket has moved.
for rocket in my_rockets:
    print("Rocket altitude:", rocket.y)

Rocket altitude: 1
Rocket altitude: 0
Rocket altitude: 0
Rocket altitude: 0
Rocket altitude: 0

Example 6: Quaternions

We are used to working with several numeric systems, for example:

 Natural numbers: $$\mathbb{N} \rightarrow 0, 1, 2, 3, 4, \cdots \; \text{or}\;  1, 2, 3, 4, \cdots$$

Integer numbers: $$\mathbb{Z} \rightarrow \cdots, −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, \cdots$$

Rational numbers: $$\mathbb{Q} \rightarrow \frac{a}{b} \;\mathrm{where}\;  a \text{and}\; b  \in \mathbb{Z} \; \mathrm{and}\; b \neq 0$$

Real numbers: $$\mathbb{R} \rightarrow \text{The limit of a convergent sequence of rational numbers. examples:}\;  \pi=3.1415..., \phi=1.61803..., etc$$

Complex numbers: $$\mathbb{C} \rightarrow a + b i \;\text{or}\; a +  i b \;\text{where}\; a \;\text{and}\; b \in \mathbb{R} \;\text{and}\; i=\sqrt{−1}$$

There are, however other sets of numbers, some of them are called hypercomplex numbers. They include the Quaternions $\mathbb{H}$, invented by Sir William Rowan Hamilton, in which multiplication is not commutative, and the Octonions $\mathbb{O}$, in which multiplication is not associative.

The use of these types of numbers is quite broad but maybe the most important use comes from engineering and computer description of moving objects, as they can be used to represent transformations of orientations of graphical objects. They are also used in Quantum Mechanics in the case of Spinors.

We will use the Quaternions as an excuse to introduce key concepts in object-oriented programming using Python. Complex numbers can be thought of as tuples of real numbers. Every complex is a real linear combination of the unit complex:

[\lbrace e_0, e_1, \rbrace]

There are rules about how to multiply complex numbers. They can be expressed in the following table:

$\times$	$1$	$i$
$1$	$1$	$i$
$i$	$i$	$-1$

Similarly, Quaternions can be thought of as 4-tuples of real numbers. Each Quaternion is a real linear combination of the unit quaternion set:

[\lbrace e_0, e_1, e_2, e_3 \rbrace]

The rules about how to multiply Quaternions are different from Complex and Reals. They can be expressed in the following table:

$\times$	$1$	$i$	$j$	$k$
$1$	$1$	$i$	$j$	$k$
$i$	$i$	$-1$	$k$	$-j$
$j$	$j$	$-k$	$-1$	$i$
$k$	$k$	$j$	$-i$	$-1$

Our objective is to create a Python Class that could deal with Quaternions as simple and direct as possible. A class is a concept from Object-Oriented programming that allows to abstract the idea of an object. An object is something that has properties and can do things. In our case, we will create a class Quaternion. Instances of the class will be specific quaternions. We can do things with quaternions such as add two quaternions and multiply them using the multiplication rule above, we can do pretty much the same kind of things that we can expect from complex numbers but in a rather more elaborated way. Let us create a first our first version of the class Quaternion and we will improve it later on.

from numbers import Number
from math import sqrt

class Quaternion():
    
    def __init__(self,value=None):
        if value is None:
            self.values = tuple((0,0,0,0))
        elif isinstance(value,(int,float)):
            self.values = tuple((value, 0, 0, 0))
        elif isinstance(value,complex):
            self.values = tuple((value.real, value.imag, 0, 0))
        elif isinstance(value,(tuple, list)):
            self.values = tuple(value)

    def __eq__(self,other):
        if isinstance(other, Number):
            other= self.__class__(other)
        return self.values == other.values
        
    __req__ = __eq__
            
    
    def __str__(self):
        sigii = '+' if self.values[1] >= 0 else '-'
        sigjj = '+' if self.values[2] >= 0 else '-'
        sigkk = '+' if self.values[3] >= 0 else '-'
        return "%.3f %s %.3f i %s %.3f j %s %.3f k" % ( self.values[0], sigii, abs(self.values[1]), sigjj, abs(self.values[2]), sigkk, abs(self.values[3])) 
        
    def __repr__(self):
        return 'Quaternion('+str(self.values)+')'

    @property
    def scalar_part(self):
        return self.values[0]
    
    @property
    def vector_part(self):
        return self.values[1:]

    @staticmethod
    def one():
        return Quaternion((1,0,0,0))

    @staticmethod
    def ii():
        return Quaternion((0,1,0,0))
    
    @staticmethod
    def jj():
        return Quaternion((0,0,1,0))

    @staticmethod
    def kk():
        return Quaternion((0,0,0,1))
    
    def __add__(self, other):
        if isinstance(other, Number):
            other = self.__class__(other)
        ret=[0,0,0,0]
        for i in range(4):
            ret[i]=self.values[i]+other.values[i]
        return self.__class__(ret)
    
    __radd__ = __add__

    
    def __mul__(self, other):
        if isinstance(other, Number):
            other = self.__class__(other)
        ret = [0,0,0,0]
        ret[0] = self.values[0]*other.values[0]-self.values[1]*other.values[1]-self.values[2]*other.values[2]-self.values[3]*other.values[3]
        ret[1] = self.values[0]*other.values[1]+self.values[1]*other.values[0]+self.values[2]*other.values[3]-self.values[3]*other.values[2]
        ret[2] = self.values[0]*other.values[2]+self.values[2]*other.values[0]+self.values[3]*other.values[1]-self.values[1]*other.values[3]
        ret[3] = self.values[0]*other.values[3]+self.values[3]*other.values[0]+self.values[1]*other.values[2]-self.values[2]*other.values[1]
        return self.__class__(ret)

    def __rmul__(self, other):
        if isinstance(other, Number):
            other= self.__class__(other)
        ret = [0,0,0,0]
        ret[0] = self.values[0]*other.values[0]-self.values[1]*other.values[1]-self.values[2]*other.values[2]-self.values[3]*other.values[3]
        ret[1] = self.values[0]*other.values[1]+self.values[1]*other.values[0]-self.values[2]*other.values[3]+self.values[3]*other.values[2]
        ret[2] = self.values[0]*other.values[2]+self.values[2]*other.values[0]-self.values[3]*other.values[1]+self.values[1]*other.values[3]
        ret[3] = self.values[0]*other.values[3]+self.values[3]*other.values[0]-self.values[1]*other.values[2]+self.values[2]*other.values[1]
        return self.__class__(ret)

    def norm(self):
        return sqrt(self.values[0]*self.values[0]+self.values[1]*self.values[1]+self.values[2]*self.values[2]+self.values[3]*self.values[3])
    
    def conjugate(self):
        return Quaternion((self.values[0], -self.values[1], -self.values[2], -self.values[3] ))
    
    def inverse(self):
        return self.conjugate()*(1.0/self.norm()**2)
    
    def unitary(self):
        return self*(1.0/self.norm())

Let’s explore in detail all the code above. When a new object of the class Quaternion is created the python interpreter calls the __init__ method. The values could be entered as tuple or list, internally the four values of the Quaternion will be stored in a tuple. See now some examples of Quaternions created explicitly:

Quaternion([0,2,3.7,9]) 

Quaternion((0, 2, 3.7, 9))

Quaternion((2,5,0,8))

Quaternion((2, 5, 0, 8))

Quaternion()

Quaternion((0, 0, 0, 0))

Quaternion(3)

Quaternion((3, 0, 0, 0))

Quaternion(3+4j)

Quaternion((3.0, 4.0, 0, 0))

The text in the output is a representation of the object Quaternion. This representation is obtained by the python interpreter by calling the __repr__ method. The __repr__ (also used as repr() ) method is intended to create an eval()-usable string of the object. You can see that in the next example:

a=Quaternion((2, 5, 0, 8))
repr(a)

'Quaternion((2, 5, 0, 8))'

b=eval(repr(a))
repr(b)

'Quaternion((2, 5, 0, 8))'

We create a new Quaternion b using the representation of Quaternion a. We can also test that a and b are equal using the __eq__ method

a == b

True

In the case below we are comparing a Quaternion with an Integer, the method __eq__ will first create a new Quaternion from the Integer and after will test for equality

Quaternion((3,0,0,0)) == 3

True

This example is rather different a complex number has no method to compare with Quaternion, so it will try to use the reverse equality __req__. As the equality is symmetric for Quaternions the line __req__ = __eq__ is making the method __req__ referencing the method __eq__ with reverse arguments

3+4j == Quaternion((3,4,0,0))

True

Similarly as a complex number is composed of real and imaginary parts, a quaternion is can be decomposed of a scalar and vector part. We can create methods to return those parts. We add two methods scalar_part and vector_part to return the corresponding elements of the quaternion. The text @property is a decorator, this special decorator makes those methods look like read-only variables when in fact they are slices of the internal variable self.values. Notice that when we are calling the properties scalar_part and vector_part the parenthesis are no longer present

Quaternion((2, 5, 0, 8))

b.scalar_part

b.vector_part

(5, 0, 8)

The elements of this basis are customarily denoted as 1, i, j, and k. Every element of $\mathbb{H}$ can be uniquely written as a linear combination of these basis elements, that is, as a 1 + b i + c j + d k, where a, b, c, and d are real numbers. The basis element 1 will be the identity element of $\mathbb{H}$, meaning that multiplication by 1 does nothing, and for this reason, elements of H are usually written a 1 + b i + c j + d k, suppressing the basis element 1. Let us create the elements of the base using the four static methods that we defined above as one, ii, jj, kk. Those methods are very special. First, they are decorated using @staticmethod indicating that they are called without an instance. For that reason, the argument self does not appear in the list of arguments. See above how they are used here to create our 4 unitary Quaternions

one=Quaternion().one()
iii=Quaternion().ii()
jjj=Quaternion().jj()
kkk=Quaternion().kk()

There is another interesting method that we will use here. It is the __str__. The method __str_ is similar to __repr__ in the sense that both produces string representations of the object, but __str__ is intended to be human readable but __repr__ should be eval()-able

print(one)
print(iii)
print(jjj)
print(kkk)

000 + 0.000 i + 0.000 j + 0.000 k
000 + 1.000 i + 0.000 j + 0.000 k
000 + 0.000 i + 1.000 j + 0.000 k
000 + 0.000 i + 0.000 j + 1.000 k

The sum of quaternions is very straightforward. We implement the sum of quaternions using the special method __add__ and __radd__. The first one is used in cases where the first argument is a quaternion

print(iii+jjj)

0.000 + 1.000 i + 1.000 j + 0.000 k

Also for computing sums of quaternions with other numbers using an internal conversion to quaternion. Notice that complex numbers in python use the symbol j instead of i. But the __str__ method is creating a string traditionally, printing I to indicate the imaginary component.

print(kkk+ 3 + 7j)

3.000 + 7.000 i + 0.000 j + 1.000 k

The reverse operation __radd__ is used in cases where the direct operation fails. The complex number class has no method to add quaternions, so python will try the reverse operation __radd__ instead, in this case, quaternions are commutative under addition, so we are making __radd__ equivalent to __add__ . Also notice that we can chain the sum of quaternions in a very natural way

print(9 + 4j + iii + kkk)

9.000 + 5.000 i + 0.000 j + 1.000 k

The multiplication is rather different. Lets for example test the defining property of Quaternions: $i^2=j^2=k^2=ijk=-1$

print(iii*iii)
print(jjj*jjj)
print(kkk*kkk)
print(iii*jjj*kkk)

-1.000 + 0.000 i + 0.000 j + 0.000 k
-1.000 + 0.000 i + 0.000 j + 0.000 k
-1.000 + 0.000 i + 0.000 j + 0.000 k
-1.000 + 0.000 i + 0.000 j + 0.000 k

This was possible by using the special method __mul__. As the right-side object is a quaternion, it will call the __mul__ with the left-hand side being the other argument. That is also the case for a quaternion multiplied by any other number:

a=8 + iii*7 + jjj*6 + kkk*5
print(a)

8.000 + 7.000 i + 6.000 j + 5.000 k

Being able to multiply a number for a quaternion requires the reverse operation and this is not the same as the direct one because quaternions do not commute under multiplication, see for example:

print(2*a)

16.000 + 14.000 i + 12.000 j + 10.000 k

print(1j*a)

-7.000 + 8.000 i - 5.000 j + 6.000 k

print(a*1j)

-7.000 + 8.000 i + 5.000 j - 6.000 k

There are four more methods to complete a simple but effective Quaternion class implementation. They are the conjugate, the norm, the inverse, and the unitary quaternion (also called versor). They were written at the end of our code. Let’s test those simple methods. Let’s take b from a previous calculation:

b=2*a
print(b)

16.000 + 14.000 i + 12.000 j + 10.000 k

The norm of the quaternion is:

b.norm()

26.38181191654584

The unitary quaternion:

b.unitary()

Quaternion((0.6064784348631227, 0.5306686305052324, 0.454858826147342, 0.37904902178945166))

b.unitary()*b.norm()

Quaternion((16.0, 14.0, 12.0, 10.0))

Now we show that we can decompose a quaternion in its versor scaled by its norm

b == b.norm()*b.unitary()

True

As quaternions are not commutative, the division express as $\frac{a}{b}$. Using that expression we cannot make the difference between $a b^{-1}$ or $a^{-1} b$ and those two quaternions are in general not the same. We will see that with an example

c= 1 + 2*iii + 3*jjj + 4*kkk
print(b)
print(c)

16.000 + 14.000 i + 12.000 j + 10.000 k
1.000 + 2.000 i + 3.000 j + 4.000 k

print(b.inverse() * c)

0.172 + 0.000 i + 0.103 j + 0.052 k

print(b * c.inverse())

4.000 - 1.200 i + 0.000 j - 2.400 k

The inverse works as expected creating a unitary quaternion when multiplied with the original quaternion. At least under the precision of floating point numbers

(b * b.inverse()).norm()

0.9999999999999999

Some references about quaternions

Quaternions, Octonions and Sextenions had an interesting evolution even if they remain unknown for many people out of mathematicians and theoretical physicist. You can learn more about the quaternions in the Wikipedia. Another good source of reference is the Wolfram’s Mathworld page.

Notes about implementation

This implementation was done in pure python code, avoiding the use of NumPy on purpose. There are several ways in which the implemented class could be improved by adding more special methods and generalizing others. They are also alternative representations for quaternions, for example using $2 \times 2$ matrices with complex elements or $4 \times 4$ matrices on Reals. each of them with its advantages and disadvantages.

Decorators, Static methods, Class methods, and Properties (Advanced)

A method is a function that is stored as a class attribute. You can declare and access such a function this way:

from math import pi

class Sphere(object):

    def __init__(self, r):
        self.radius = r

    def get_area(self):
        return 4*pi*self.radius**2

    def get_volume(self):
        return 4/3*pi*self.radius**3
    

Sphere.get_volume

<function __main__.Sphere.get_volume(self)>

We can’t call get_volume because it’s not bound to any instance of Sphere. And a method wants an instance as its first argument (in Python 3 it could be anything). Let’s try to do that then:

Sphere.get_volume(Sphere(1))

4.1887902047863905

It worked! We called the method with an instance as its first argument, so everything’s fine. But you will agree with me if I say this is not a very handy way to call methods; we have to refer to the class each time we want to call a method. And if we don’t know what class is our object, this is not going to work for very long.

So what Python does for us, is that it binds all the methods from the class Sphere to any instance of this class. This means that the attribute get_volume of an instance of Sphere is a bound method: a method for which the first argument will be the instance itself.

Sphere(2).get_volume

<bound method Sphere.get_volume of <__main__.Sphere object at 0x1387701d0>>

Sphere(2).get_volume()

33.510321638291124

As expected, we don’t have to provide any argument to get_volume, since it’s bound, its self argument is automatically set to our Sphere instance. Here’s an even better proof of that:

m = Sphere(2).get_volume
m()

33.510321638291124

Indeed, you don’t even have to keep a reference to your Sphere object. Its method is bound to the object, so the method is sufficient for itself.

But what if you wanted to know which object this bound method is bound to? Here’s a little trick:

m = Sphere(2).get_volume
m.__self__

<__main__.Sphere at 0x138831ad0>

# You could guess, look at this:
m == m.__self__.get_volume

True

We still have a reference to our object, and we can find it back if we want.

In Python 3, the functions attached to a class are not considered as an unbound method anymore, but as simple functions, that are bound to an object if required. So the principle stays the same, the model is just simplified.

Sphere.get_volume

<function __main__.Sphere.get_volume(self)>

Static methods

Static methods are a special case of methods. Sometimes, you’ll write code that belongs to a class, but that doesn’t use the object itself at all. For example:

class Sphere(object):

    @staticmethod
    def double_radius(x):
        return 2*x

    def enlarge(self):
        return self.double_radius(self.radius)

In such a case, writing double_radius as a non-static method would work too, but it would provide it with a self argument that would not be used. Here, the decorator @staticmethod buys us several things:

Python doesn’t have to instantiate a bound-method for each Sphere object we instantiate.
Bound methods are objects too, and creating them has a cost.

Having a static method avoids that:

Sphere().enlarge is Sphere().enlarge

False

Sphere().double_radius is Sphere.double_radius

True

Sphere().double_radius is Sphere().double_radius

True

It eases the readability of the code: seeing @staticmethod, we know that the method does not depend on the state of the object itself;
It allows us to override the mix_ingredients method in a subclass. If we used a function mix_ingredients defined at the top-level of our module, a class inheriting from Sphere wouldn’t be able to change the way we mix ingredients for our Sphere without overriding cook itself.

Class methods

Class methods are methods that are not bound to an object, but a class

class Sphere(object):
    radius = 2

    @classmethod
    def get_radius(cls):
        return cls.radius

Sphere.get_radius

<bound method Sphere.get_radius of <class '__main__.Sphere'>>

Sphere().get_radius

<bound method Sphere.get_radius of <class '__main__.Sphere'>>

Sphere.get_radius == Sphere.get_radius

True

Sphere.get_radius()

Whatever the way you use to access this method, it will always be bound to the class it is attached to, and its first argument will be the class itself (remember that classes are objects too).

Class methods are most useful for two types of methods:

Factory methods, that is used to create an instance for a class using for example some sort of pre-processing. If we use a @staticmethod instead, we would have to hardcode the Sphere class name in our function, making any class inheriting from Sphere unable to use our factory for its use.

class Sphere(object):
    def __init__(self, r):
        self.radius = r

    @classmethod
    def scale_radius(cls, x):
        return cls(2*x)

s=Sphere.scale_radius(2)
s.radius

Static methods calling static methods: if you split a static method into several static methods, you shouldn’t hard-code the class name but use class methods. Using this way to declare our method, the Sphere name is never directly referenced and inheritance and method overriding will work flawlessly

from math import pi

class Sphere(object):
    
    def __init__(self, radius, height):
        self.radius = radius
        self.height = height

    def get_area(self):
        return compute_area(self.radius)

    def get_volume(self):
        return compute_area(self.radius)
    
    @staticmethod
    def compute_area(radius):
         return 4*pi*radius**2

    @staticmethod
    def compute_volume(radius):
         return 4/3*pi*radius**3

    @classmethod
    def ratio(cls, radius):
        return cls.compute_area(radius)/cls.compute_volume(radius)
    

Sphere.ratio(10)

0.3

Abstract methods

An abstract method is a method defined in a base class, but that may not provide any implementation. In Java, it would describe the methods of an interface.

So the simplest way to write an abstract method in Python is:

class Sphere(object):
    def get_radius(self):
        raise NotImplementedError

Any class inheriting from Sphere should implement and override the get_radius method, otherwise an exception would be raised.

This particular way of implementing abstract method has a drawback. If you write a class that inherits from Sphere and forgets to implement get_radius, the error will only be raised when you’ll try to use that method. Sphere() <main.Sphere object at 0x7fb747353d90>

Sphere().get_radius() Traceback (most recent call last): File “", line 1, in File "", line 3, in get_radius NotImplementedError There's a way to trigger this way earlier, when the object is being instantiated, using the abc module that's provided with Python.

from abc import ABC, abstractmethod

class SurfaceRevolution(ABC):

    def __init__(self,r):
        self.radius = r
    
    @abstractmethod
    def get_radius(self):
         """Method that should do something."""

Using abc and its special class, as soon as you’ll try to instantiate SurfaceRevolution or any class inheriting from it, you’ll get a TypeError.

##
## SurfaceRevolution(4)
## ---------------------------------------------------------------------------
## TypeError                                 Traceback (most recent call last)
## <ipython-input-269-02ffabd7c877> in <module>
## ----> 1 SurfaceRevolution(4)
## 
## TypeError: Can't instantiate abstract class SurfaceRevolution with abstract methods get_radius

Mixing static, class and abstract methods

When building classes and inheritances, the time will come where you will have to mix all these methods decorators. So here are some tips about it.

Keep in mind that declaring a method as being abstract, doesn’t freeze the prototype of that method. That means that it must be implemented, but it can be implemented with any argument list.

import abc

class SurfaceRevolution(object):
    __metaclass__  = abc.ABCMeta

    @abc.abstractmethod
    def get_radius(self):
         """Returns the radius list."""

class Spheroid(SurfaceRevolution):
    def get_radius(self, scaled=False):
        center = 2 if scaled else 1
        return scaled * self.radius

This is valid since Spheroid fulfills the interface requirement we defined for SurfaceRevolution objects. That means that we could also implement it as a class or a static method, for example:

from abc import ABC, abstractmethod

class SurfaceRevolution(ABC):

    @abstractmethod
    def get_center(self):
         """Returns the center."""

class CenteredSphere(SurfaceRevolution):
    @staticmethod
    def get_center():
        return (0,0,0)

CenteredSphere.get_center()

(0, 0, 0)

This is also correct and fulfills the contract we have with our abstract SurfaceRevolution class. The fact that the get_center method doesn’t need to know about the object to return the result is an implementation detail, not a criterion to have our contract fulfilled.

Therefore, you can’t force implementation of your abstract method to be a regular, class, or static method, and arguably you shouldn’t. Starting with Python 3, it’s now possible to use the @staticmethod and @classmethod decorators on top of @abstractmethod:

from abc import ABC, abstractmethod

class SurfaceRevolution(ABC):

    centered = True

    @classmethod
    @abstractmethod
    def is_centered(cls):
         """Returns the ingredient list."""
         return cls.centered

Don’t misread this: if you think this is going to force your subclasses to implement is_centered as a class method, you are wrong. This simply implies that your implementation of is_centered in the SurfaceRevolution class is a class method.

An implementation in an abstract method? Yes! In Python, contrary to methods in Java interfaces, you can have code in your abstract methods and call it via super():

from abc import ABC, abstractmethod

class SurfaceRevolution(ABC):

    center = (0,0,0)

    @classmethod
    @abstractmethod
    def get_center(cls):
         """Returns the ingredient list."""
         return cls.center

class MovedSphere(SurfaceRevolution):
    def get_center(self):
        return super(MovedSphere, self).get_center()

In such a case, every Sphere you will build by inheriting from SurfaceRevolution will have to override the get_center method, but will be able to use the default mechanism to get the center by using super().

Properties

In Python methods can act like properties when using the @property decorator Properties are used in Python Object Oriented Programming to provide the class with values that result from computations from internal properties that we want to keep private.

The example below shows the usage of properties to store the value of temperature and control that is value has the physical sense

class Celsius:
    def __init__(self, temperature = 0):
        self._temperature = temperature

    def to_fahrenheit(self):
        return (self.temperature * 1.8) + 32

    @property
    def temperature(self):
        print("Getting value")
        return self._temperature

    @temperature.setter
    def temperature(self, value):
        if value < -273:
            raise ValueError("Temperature below -273 is not possible")
        print("Setting value")
        self._temperature = value

c=Celsius(100)

c.temperature

Getting value

100

c.to_fahrenheit()

Getting value

212.0

## c.temperature=-300
## ---------------------------------------------------------------------------
## ValueError                                Traceback (most recent call last)
## <ipython-input-318-dcba37e43336> in <module>
## ----> 1 c.temperature=-300
## 
## <ipython-input-309-c16b585d1af3> in temperature(self, value)
##     14     def temperature(self, value):
##     15         if value < -273:
## ---> 16             raise ValueError("Temperature below -273 is not possible")
##     17         print("Setting value")
##     18         self._temperature = value
##
## ValueError: Temperature below -273 is not possible

Example 7: Platonic Solids

We will use some classes to manipulate some of the properties of Platonic Solids

As you know there are 5 platonic Solids and they shared some combinatorial properties.

A convex polyhedron is a Platonic solid if and only if

all its faces are congruent convex regular polygons
none of its faces intersect except at their edges, and
the same number of faces meet at each of its vertices.

Each Platonic solid can therefore be denoted by a symbol {$p$, $q$} where

$p$ is the number of edges (or, equivalently, vertices) of each face, and
$q$ is the number of faces (or, equivalently, edges) that meet at each vertex.

The symbol {$p$ , $q$}, called the Schläfli symbol, give a combinatorial description of the polyhedron. The Schläfli symbols of the five Platonic solids are given in the table below.

Polyhedron	Vertices	Edges	Faces	Schläfli symbol	Vertex configuration
Tetrahedron	4	6	4	{3, 3}	3.3.3
Hexahedron	8	12	6	{4, 3}	4.4.4
Octahedron	6	12	8	{3, 4}	3.3.3.3
Dodecahedron	20	30	12	{5, 3}	5.5.5
Icosahedron	12	30	20	{3, 5}	3.3.3.3.3

All other combinatorial information about these solids, such as the total number of vertices ($V$), edges ($E$), and faces ($F$), can be determined from $p$ and $q$. Since any edge joins two vertices and has two adjacent faces we must have:

\begin{equation} pF = 2E = qV.\, \end{equation}

The other relationship between these values is given by Euler’s formula:

\begin{equation} V - E + F = 2.\, \end{equation}

Together these three relationships completely determine ‘‘V’’, ‘‘E’’, and ‘‘F’’:

\begin{equation} V = \frac{4p}{4 - (p-2)(q-2)},\quad E = \frac{2pq}{4 - (p-2)(q-2)},\quad F = \frac{4q}{4 - (p-2)(q-2)}. \end{equation}

Swapping $p$ and $q$ interchanges $F$ and $V$ while leaving $E$ unchanged.

Every polyhedron has a dual (or “polar”) polyhedron with faces and vertices interchanged. The dual of every Platonic solid is another Platonic solid so that we can arrange the five solids into dual pairs.

The tetrahedron is self-dual (i.e. its dual is another tetrahedron).
The cube and the octahedron form a dual pair.
The dodecahedron and the icosahedron form a dual pair.

We can now encode all this knowledge into a Python class that allows us to manipulate platonic solids. We will explore the Vertex, Edges, and Face relations and the duality relation

class PlatonicSolid():
    
    platonic={'tetrahedron': (3,3), 'hexahedron': (4,3), 'octahedron': (3,4), 
              'dodecahedron': (3,5), 'icosahedron': (5,3)}
    
    def __init__(self, name=None):
        
        if name is None:
            self.schlafli = (3,3)
        else:
            self.schlafli = self.name2schlafi(name)

    @classmethod
    def name2schlafi(cls,name):
        
        if name.lower() == 'cube':
            hedron = 'hexahedron'
        elif name.lower() in cls.platonic:
            hedron = name.lower()
        else:
            raise ValueError("'%s' is not recognized as a Platonic Solid" % name)
        return cls.platonic[hedron]
        
    @classmethod
    def schlafli2name(cls,schlafli):

        if schlafli not in cls.platonic.values():
            raise ValueError("'%s' is not recognized as a valid Schlafli Symbol" % schlafli)
            
        hedrons = [key  for (key, value) in cls.platonic.items() if value == schlafli]
        return hedrons[0]

    @property
    def p(self):
        return self.schlafli[0]
    
    @property
    def q(self):
        return self.schlafli[1]
    
    @property
    def vertices(self):
        p = self.p
        q = self.q
        return 4*p//(4 - (p-2)*(q-2))
    
    @property
    def edges(self):
        p = self.p
        q = self.q
        return 2*p*q//(4 - (p-2)*(q-2))
    
    @property
    def faces(self):
        p = self.p
        q = self.q
        return 4*q//(4 - (p-2)*(q-2))
    
    def dual(self):
        return self.__class__(self.schlafli2name((self.q,self.p)))
        

cube=PlatonicSolid('cube')
print(cube.schlafli)
print(cube.vertices)
print(cube.edges)
print(cube.faces)

(4, 3)
8
12
6

octa=cube.dual()
print(octa.schlafli)
print(octa.vertices)
print(octa.edges)
print(octa.faces)

(3, 4)
6
12
8

3 Key Differences between Python 2.x and 3.x

Print

Python 2’s print statement has been replaced by the print() function, meaning that we have to wrap the object that we want to print in parentheses. The commands below work on Python 2.x from platform import python_version

print ‘Python’, python_version() print ‘Hello, World!’ print(‘Hello, World!’) print “text”, ; print ‘print more text on the same line’ In Python 3.x to get the same results you have to use:

from platform import python_version

print('Python', python_version())
print('Hello, World!')

print("some text,", end="")
print(' print more text on the same line')

Python 3.11.7
Hello, World!
some text, print more text on the same line

Integer Division

This change is particularly dangerous. In Scientific Computing this is even more true as the division can go unnoticed. In Python 2.x the division of two integers is always an integer. In Python 3.x the result is promoted to float if the numbers have no solution in the integers. The commands below work in Python 2.x and return integers: print ‘Python’, python_version() print ‘3 / 2 =’, 3 / 2 print ‘3 // 2 =’, 3 // 2 print ‘3 / 2.0 =’, 3 / 2.0 print ‘3 // 2.0 =’, 3 // 2.0 In Python 3.x to get the same results you have to use:

print('Python', python_version())
print('3 / 2 =', 3 / 2)
print('3 // 2 =', 3 // 2)
print('3 / 2.0 =', 3 / 2.0)
print('3 // 2.0 =', 3 // 2.0)

Python 3.11.7
/ 2 = 1.5
// 2 = 1
/ 2.0 = 1.5
// 2.0 = 1.0

xrange

xrange() used to be very popular in Python 2.x for creating an iterable object, e.g., in a for-loop or list/set-dictionary-comprehension. In many situations, you need to iterate over a list of values and xrange has the advantage of the regular range() of being generally faster if you have to iterate over it only once (e.g., in a for-loop).

There are two main reasons for choosing xrange over range, speed memory. However, in contrast to 1-time iterations, it is not recommended if you repeat the iteration multiple times, since the generation happens every time from scratch!

Consider this case:

import timeit

def test_range(n):
    sum=0
    for i in range(n):
        for j in range(n):
            for k in range(n):
                ijk=i+j*k
                sum=sum+ ijk
                
                if ijk > 1:
                    break

            else:
                # Continue if the inner loop wasn't broken.
                continue
            # Inner loop was broken, break the outer.
            break

        else:
            # Continue if the inner loop wasn't broken.
            continue
        # Inner loop was broken, break the outer.
        break


    return sum
            
def test_xrange(n):
    sum=0
    for i in xrange(n):
        for j in xrange(n):
            for k in xrange(n):
                ijk=i+j*k
                sum=sum+ ijk
                
                if ijk > 1:
                    break

            else:
                # Continue if the inner loop wasn't broken.
                continue
            # Inner loop was broken, break the outer.
            break

        else:
            # Continue if the inner loop wasn't broken.
            continue
        # Inner loop was broken, break the outer.
        break

    return sum

These two functions are used on the script range_vs_xrange.py and their timings are shown: $ python2 range_vs_xrange.py Using range() function: 1.72167515755 Using xrange() function: 1.00023412704

On Python 3.x the xrange was removed and range behaves as xrange returning an iterable object.

More differences

There are more differences beyond the 3 above, a good description of the key differences can be found on Sebastian Raschka’s blog

Example 9: Life Game

import numpy as np
from pandas import DataFrame
import matplotlib.pyplot as plt
#import time

def conway_life(len=100, wid=100, gen=5):
     
    curr_gen = DataFrame(np.random.randint(0, 2, (len+2, wid+2)),
                         index = range(len+2), 
                         columns = range(wid+2))
    curr_gen[0] = 0
    curr_gen[wid+1] = 0
    curr_gen[0: 1] = 0
    curr_gen[len+1: len+2] = 0    
    
    for i in range(gen):
        
        fig, ax = plt.subplots()
        draw = curr_gen[1:len+1].drop([0, wid+1], axis=1)
        
        image = draw
        ax.imshow(image, cmap=plt.cm.cool, interpolation='nearest')
        ax.set_title("Conway's game of life.")
        
        # Move left and bottom spines outward by 10 points
        ax.spines['left'].set_position(('outward', 10))
        ax.spines['bottom'].set_position(('outward', 10))
        # Hide the right and top spines
        ax.spines['right'].set_visible(False)
        ax.spines['top'].set_visible(False)
        # Only show ticks on the left and bottom spines
        ax.yaxis.set_ticks_position('left')
        ax.xaxis.set_ticks_position('bottom')

        plt.axis('off')
        plt.show()
        # time.sleep(1)         
        
        next_gen = DataFrame(np.random.randint(0, 1, (len+2, wid+2)),
                             index = range(len+2), 
                             columns = range(wid+2))
        
        for x in range(1, wid+1):
            for y in range(1, len+1):
                env = (curr_gen[x-1][y-1] + curr_gen[x][y-1] + 
                       curr_gen[x+1][y-1]+ curr_gen[x-1][y] + 
                       curr_gen[x+1][y] + curr_gen[x-1][y+1] + 
                       curr_gen[x][y+1] + curr_gen[x+1][y+1])
            
                if (not curr_gen[x][y] and env == 3):
                    next_gen[x][y] = 1
                if (curr_gen[x][y] and env in (2, 3)):
                    next_gen[x][y] = 1
                
        curr_gen = next_gen 

conway_life()

png

Conclusions

In this notebook we explore:

Introduction
1. Zen of Python
2. Optimization
Python Syntax I
1. Variables
2. Data Types
3. Mathematical Operations
Python Syntax II
1. Containers
2. Loops
3. Conditionals
Python Syntax III
1. Functions
Python Syntax IV
1. Classes
Differences between Python 2.x and 3.x
1. Print
2. Integer division

Acknowledgments and References

This Notebook has been adapted by Guillermo Avendaño (WVU), Jose Rogan (Universidad de Chile) and Aldo Humberto Romero (WVU) from the Tutorials for Stanford cs228 and cs231n. A large part of the info was also built from scratch. In turn, that material was adapted by Volodymyr Kuleshov and Isaac Caswell from the CS231n Python tutorial by Justin Johnson (http://cs231n.github.io/python-numpy-tutorial/). Another good resource, in particular, if you want to just look for an answer to specific questions is planetpython.org, in particular for data science.

Changes to the original tutorial include strict Python 3 formats and a split of the material to fit a series of lessons on Python Programming for WVU’s faculty and graduate students.

The support of the National Science Foundation and the US Department of Energy under projects: DMREF-NSF 1434897, NSF OAC-1740111, and DOE DE-SC0016176 is recognized.

Back of the Book

plt.figure(figsize=(3,3))
n = chapter_number
maxt=(2*(n-1)+3)*np.pi/2
t = np.linspace(np.pi/2, maxt, 1000)
tt= 1.0/(t+0.01)
x = (maxt-t)*np.cos(t)**3
y = t*np.sqrt(np.abs(np.cos(t))) + np.sin(0.3*t)*np.cos(2*t)
plt.plot(x, y, c="green")
plt.axis('off');

png

end = time.time()
print(f'Chapter {chapter_number} run in {int(end - start):d} seconds')

Chapter 1 run in 24 seconds

Key Points

Python is an easy-to-learn programming language.

Python Scripting for HPC

Overview

Teaching: 45 min
Exercises: 15 min

Topics

Why learn Python programming language?

How can I use Python to write small scripts?

Objectives

Learn about variables, loops, conditionals and functions

Python Programming for Scientists in a hurry

Chapter 2. Standard Library

Guillermo Avendaño Franco
Aldo Humberto Romero

List of Notebooks

Language Syntax
Standard Library [This notebook]
Scientific Packages
Numpy
Matplotlib
SciPy
Pandas
Cython
Parallel Computing

Setup

%load_ext watermark

%watermark

Last updated: 2024-07-25T19:10:56.785117-04:00

Python implementation: CPython
Python version       : 3.11.7
IPython version      : 8.14.0

Compiler    : Clang 12.0.0 (clang-1200.0.32.29)
OS          : Darwin
Release     : 20.6.0
Machine     : x86_64
Processor   : i386
CPU cores   : 8
Architecture: 64bit

import time
start = time.time()
chapter_number = 2
import matplotlib
%matplotlib inline
%load_ext autoreload
%autoreload 2

import numpy as np
import matplotlib.pyplot as plt

%watermark -iv

matplotlib: 3.8.2
numpy     : 1.26.2

Python Standard Library

Introduction
Module sys
Modules math and cmath
Modules os and os.path
Module shutil
Module itertools
Module json
Module subprocess
module multiprocessing

Introduction

The Python Standard Library (PSL) is a set of modules distributed with Python and they are included in most Python implementations. With some very specific exceptions, you can take for granted that every machine capable of running Python code will have those modules available too.

The Python’s standard library is very extensive. The library contains built-in modules (written in C) that provide access to system functionality such as file I/O that would otherwise be inaccessible to Python programmers, as well as modules written in Python that provide standardized solutions for many problems that occur in everyday programming. The idea we are trying to use here is that the existence of some modules will help with the simplicity of the program and they will allow also portability between different systems. Python is trying to create a natural neutral platform for application programming interfaces (APIs).

Here we are making a selection of a few modules that are commonly used in Scientific Computing. The selection itself is rather subjective but from experience, most users using Python for research, especially numerical-oriented calculations will use at some point several of these modules.

The complete documentation about these modules can be found here

Module `sys`

This module provides access to some variables used or maintained by the interpreter and to functions that interact strongly with the interpreter. It is always available. More info can be found in sys

import sys

There are a few reasons to include this module in the selection, consider getting the version of Python that is in use:

sys.version

'3.11.7 (main, Dec 24 2023, 07:47:18) [Clang 12.0.0 (clang-1200.0.32.29)]'

sys.version_info

sys.version_info(major=3, minor=11, micro=7, releaselevel='final', serial=0)

To know information about the limits of float type. sys.float_info contains low-level information about the precision and internal representation. The values correspond to the various floating-point constants defined in the standard header file float.h for the ‘C’ programming language; see section 5.2.4.2.2 of the 1999 ISO/IEC C standard [C99], ‘Characteristics of floating types’, for details.

sys.float_info

sys.float_info(max=1.7976931348623157e+308, max_exp=1024, max_10_exp=308, min=2.2250738585072014e-308, min_exp=-1021, min_10_exp=-307, dig=15, mant_dig=53, epsilon=2.220446049250313e-16, radix=2, rounds=1)

Each value can be retrieved independently like

sys.float_info.max

1.7976931348623157e+308

Similarly for integers:

sys.int_info

sys.int_info(bits_per_digit=30, sizeof_digit=4, default_max_str_digits=4300, str_digits_check_threshold=640)

To get the size of any object in bytes:

a=list(range(1000))
sys.getsizeof(a)

b=range(1000)
sys.getsizeof(b)

By itself, the builtin function sys.getsizeof() does not help determine the size of a container (a given object) and all of its contents, but can be used with a recipe like this to recursively collect the contents of a container.

To know the paths to search for modules

sys.path

['/Users/guilleaf/Documents/GitHub/Notebooks_4SIAH/Python',
 '/opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python311.zip',
 '/opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11',
 '/opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/lib-dynload',
 '',
 '/Users/guilleaf/Library/Python/3.11/lib/python/site-packages',
 '/opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages']

Prefix path where the current version of Python is in use:

sys.prefix

'/opt/local/Library/Frameworks/Python.framework/Versions/3.11'

To collect arguments such as

myscript.py arg1 arg2 arg3

from the command line, sys.argv can be used, in particular for scripts.

sys.argv

['/opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages/ipykernel_launcher.py',
 '-f',
 '/Users/guilleaf/Library/Jupyter/runtime/kernel-b2ee4d39-5d1d-4166-902d-90360006ed51.json']

However, sys.argv is very primitive for practical purposes. The module argparse is the recommended module to parse arguments from the command line.

Modules `math` and `cmath`

This module provides access to the mathematical functions defined by the C standard. A similar module for complex numbers is cmath

import math
import cmath

The arguments for the functions in math and cmath must be numbers. As we will see in the lesson for NumPy when the functions have to operate over multiple numbers the functions on NumPy are a far more efficient alternative and avoid expensive loops over lists or other low-performance containers.

A few functions are shown as examples:

math

math.ceil(2.5)

math.fabs(-3.7)

3.7

fabs only works for real numbers and returns always a floating point number even if the argument is integer. In the case of complex numbers the built-in abs() returns the magnitude of the complex number

abs(-1.7+4.5j)

4.810405388322278

GCD stands for Greatest Common Divisor of the integers a and b.

math.gcd(91, 133)

math.sqrt(256)

16.0

math.cos(math.pi/3)

0.5000000000000001

cmath

cmath.sqrt(-256)

16j

cmath.cos(1j*math.pi/3)

(1.600286857702386-0j)

Modules `os` and `os.path`

Sooner or later you will interact with files and folders. The module os not only provides basic operativity over the filesystem but also allows us to gain information about the operating system that is executing Python

os

import os

The module os, provides operating system-dependent functionality. Some functions are not available in some Operating Systems returning os.OSError in those cases.

os.name

'posix'

os.environ

environ{'TERM_PROGRAM': 'Apple_Terminal',
        'SHELL': '/bin/zsh',
        'TERM': 'xterm-color',
        'TMPDIR': '/var/folders/1m/dc_l_kx53tv3qkygf1r7pnmc0000gn/T/',
        'TERM_PROGRAM_VERSION': '440',
        'TERM_SESSION_ID': 'FF04BCC3-7FD5-4F11-AD59-F0BB8196132C',
        'USER': 'guilleaf',
        'SSH_AUTH_SOCK': '/private/tmp/com.apple.launchd.b46iLsbxXw/Listeners',
        'PATH': '/Users/guilleaf/miniconda3/bin:/opt/local/bin:/opt/local/sbin:/Users/guilleaf/Library/Python/3.11/bin:/usr/local/bin:/usr/bin:/bin:/usr/sbin:/sbin:/usr/local/zfs/bin:/opt/X11/bin:/Library/Apple/usr/bin:/Users/guilleaf/Library/Python/3.9/bin',
        '__CFBundleIdentifier': 'com.apple.Terminal',
        'PWD': '/Users/guilleaf',
        'XPC_FLAGS': '0x0',
        'XPC_SERVICE_NAME': '0',
        'SHLVL': '1',
        'HOME': '/Users/guilleaf',
        'LOGNAME': 'guilleaf',
        'DISPLAY': '/private/tmp/com.apple.launchd.KV7LFSdvGQ/org.xquartz:0',
        'OLDPWD': '/Volumes/SSD1TB',
        'LANG': 'en_US.UTF-8',
        '_': '/opt/local/bin/jupyter-lab-3.11',
        '__CF_USER_TEXT_ENCODING': '0x1F5:0x0:0x0',
        'GIT_PYTHON_REFRESH': 'quiet',
        'PYDEVD_USE_FRAME_EVAL': 'NO',
        'JPY_PARENT_PID': '60342',
        'CLICOLOR': '1',
        'FORCE_COLOR': '1',
        'CLICOLOR_FORCE': '1',
        'PAGER': 'cat',
        'GIT_PAGER': 'cat',
        'MPLBACKEND': 'module://matplotlib_inline.backend_inline'}

Individual environment variables can be retrieved

os.getenv('USER')

'guilleaf'

A couple of functions reproduce the effect of a few commands in Unix/Linux like pwd, cd and mkdir

# Equivalent to pwd
os.getcwd()

'/Users/guilleaf/Documents/GitHub/Notebooks_4SIAH/Python'

# Equivalent to mkdir
if not os.path.exists('test_folder'):
    os.mkdir('test_folder')

# Equivalent to cd
os.chdir('test_folder')
os.chdir('..')

# Equivalent to ls
os.listdir("test_folder")

[]

# Equivalent to rmdir
os.rmdir('test_folder')

These functions are useful in HPC to determine the number of cores on a machine

os.cpu_count()

The os module is particularly large and the functions above are just a tiny fraction of all the commands available. It is always better to use commands like os.mkdir() than to use external calls to system commands. A bad program habit is using for example:

os.system("mkdir test_folder")

This command, not only makes the code non-portable (will not work in Windows) but also on Unix systems is creating a subshell for a function that can be executed using os.mkdir()

os.path

This module implements some useful functions on pathnames. For checking the existence of a file or folder or splitting the filename from the full path

import os.path

To know if a file or folder exists:

if not os.path.exists('test_folder'):
    os.mkdir('test_folder')

os.path.isfile('test_folder')

False

os.path.isdir('test_folder')

True

fullpath=os.path.abspath('test_folder')
print(fullpath)

/Users/guilleaf/Documents/GitHub/Notebooks_4SIAH/Python/test_folder

os.path.split(fullpath)

('/Users/guilleaf/Documents/GitHub/Notebooks_4SIAH/Python', 'test_folder')

This function splits a path into two components (head, tail) where the tail is the last pathname component and the head is everything leading up to that. The tail part will never contain a slash; if the path ends in a slash, the tail will be empty.

It is useful to separate the filename from the path to that file.

Module `shutil`

For high-level operations on one or more files. Most functions in shutil support file copying and removal of multiple files from a single call. These functions are more efficient than creating loops and operate over the files individually.

import shutil

wf=open('newfile1','w')
wf.close()
if not os.path.exists('test_folder'):
    os.mkdir('test_folder')
shutil.copy2('newfile1', 'test_folder')

'test_folder/newfile1'

shutil.rmtree('test_folder')
os.remove("newfile1")

Module `itertools`

In mathematics, statistic, and machine learning, the solution of many problems can be naturally expressed using the functional programming style instead. We will discuss Python’s support for the functional programming paradigm and itertools is one of the modules in the Standard Libray to program in this style.

Combinations and permutations are often found in scientific problems. The module itertools offers efficient functions for creating iterables for those operations. Compared to actual lists, iterators can create infinite iterations, producing new elements as needed. An iterator has the advantage of using less memory than actual lists.

import itertools

Infinite iterators will create sequences of infinite length as shown below. There are two interators count() and cycle()

index=0
for i in itertools.count(13):
    print(i)
    index=index+1
    if index>9:
        break

index=0
for i in itertools.cycle('aeiou'):
    print(i)
    index=index+1
    if index>9:
        break

a
e
i
o
u
a
e
i
o
u

Finite iterators will create sequences of a predetermined length as shown below. In the itertools module you can use repeat():

for i in itertools.repeat('one',5):
    print(i)

one
one
one
one
one

For large interactions, this is more memory efficient than an equivalent:

for i in 5*['one']:
    print(i)

one
one
one
one
one

Combinatoric iterators

One of the reasons for using iterators is to produce permutations and combinations without explicitly creating long lists for evaluation. New values are generated on-the-fly which is usually far more efficient than lists.

Iterators for Combinations and Permutations can be created as follows:

for i in itertools.permutations('ABCD',3):
    print(i)

('A', 'B', 'C')
('A', 'B', 'D')
('A', 'C', 'B')
('A', 'C', 'D')
('A', 'D', 'B')
('A', 'D', 'C')
('B', 'A', 'C')
('B', 'A', 'D')
('B', 'C', 'A')
('B', 'C', 'D')
('B', 'D', 'A')
('B', 'D', 'C')
('C', 'A', 'B')
('C', 'A', 'D')
('C', 'B', 'A')
('C', 'B', 'D')
('C', 'D', 'A')
('C', 'D', 'B')
('D', 'A', 'B')
('D', 'A', 'C')
('D', 'B', 'A')
('D', 'B', 'C')
('D', 'C', 'A')
('D', 'C', 'B')

for i in itertools.combinations('ABCD',3):
    print(i)

('A', 'B', 'C')
('A', 'B', 'D')
('A', 'C', 'D')
('B', 'C', 'D')

for i in itertools.product('ABCD',repeat=2):
    print(i)

('A', 'A')
('A', 'B')
('A', 'C')
('A', 'D')
('B', 'A')
('B', 'B')
('B', 'C')
('B', 'D')
('C', 'A')
('C', 'B')
('C', 'C')
('C', 'D')
('D', 'A')
('D', 'B')
('D', 'C')
('D', 'D')

Module `json`

JSON is a lightweight data interchange format inspired by JavaScript object literal syntax. It is an effective and standard way of storing structured data. The JSON is just a format of serializing data similar to XML but more compact and easier to read for humans.

import json

Consider serializing this dictionary:

polygons={'triangle': 3, 'square': 4, 'pentagon': 5, 'hexagon': 6}

js=json.dumps(polygons)
js

'{"triangle": 3, "square": 4, "pentagon": 5, "hexagon": 6}'

This is a string that can be easily read by humans and also easily converted into a python dictionary.

poly=json.loads(js)
poly

{'triangle': 3, 'square': 4, 'pentagon': 5, 'hexagon': 6}

There are extra arguments to beautify the string, for example:

print(json.dumps(polygons, sort_keys=True, indent=4))

{
    "hexagon": 6,
    "pentagon": 5,
    "square": 4,
    "triangle": 3
}

Similar to json.dumps and json.loads there are functions to write and read JSON content directly from readable files. The functions json.dump(obj, fp, ...) and json.load(fp, ...) work on File-like objects. File-like objects have to support write() and read() like normal text file objects.

Module `subprocess`

The subprocess module allows you to spawn new processes, connect to their input/output/error pipes, and obtain their return codes. This module intends to replace several older modules and functions like os.system.

The underlying process creation and management in this module is handled by the Popen class. It offers a lot of flexibility so that developers can handle the less common cases not covered by the convenience functions.

import subprocess

sp= subprocess.Popen(["ls","-lha","/"], stdout=subprocess.PIPE, stderr=subprocess.PIPE, universal_newlines=True)

sp.wait()

The process.communicate() call reads input and output from the process. stdout is the process output. stderr will be written only if an error occurs. If you want to wait for the program to finish you can call Popen.wait().

stout, sterr = sp.communicate()

print(stout)

total 10
drwxr-xr-x  20 root  wheel   640B Jan  1  2020 [34m.[m[m
drwxr-xr-x  20 root  wheel   640B Jan  1  2020 [34m..[m[m
lrwxr-xr-x   1 root  admin    36B Jan  1  2020 [35m.VolumeIcon.icns[m[m -> System/Volumes/Data/.VolumeIcon.icns
----------   1 root  admin     0B Jan  1  2020 .file
drwxr-xr-x   2 root  wheel    64B Jan  1  2020 [34m.vol[m[m
drwxrwxr-x  68 root  admin   2.1K Jul 25 15:27 [34mApplications[m[m
drwxr-xr-x  74 root  wheel   2.3K Jun  7 20:06 [34mLibrary[m[m
drwxr-xr-x@  9 root  wheel   288B Jan  1  2020 [34mSystem[m[m
drwxr-xr-x   7 root  admin   224B Jan  1  2020 [34mUsers[m[m
drwxr-xr-x+  5 root  wheel   160B Jul 25 19:00 [34mVolumes[m[m
drwxr-xr-x@ 38 root  wheel   1.2K Jan  1  2020 [34mbin[m[m
drwxrwxr-t   2 root  admin    64B Feb 25  2019 [34mcores[m[m
dr-xr-xr-x   3 root  wheel   4.5K Jul 20 16:27 [34mdev[m[m
lrwxr-xr-x@  1 root  wheel    11B Jan  1  2020 [35metc[m[m -> private/etc
lrwxr-xr-x   1 root  wheel    25B Jul 20 16:27 [35mhome[m[m -> /System/Volumes/Data/home
drwxr-xr-x   5 root  wheel   160B Dec 31  2023 [34mopt[m[m
drwxr-xr-x   6 root  wheel   192B Jan  1  2020 [34mprivate[m[m
drwxr-xr-x@ 65 root  wheel   2.0K Jan  1  2020 [34msbin[m[m
lrwxr-xr-x@  1 root  wheel    11B Jan  1  2020 [35mtmp[m[m -> private/tmp
drwxr-xr-x@ 11 root  wheel   352B Jan  1  2020 [34musr[m[m
lrwxr-xr-x@  1 root  wheel    11B Jan  1  2020 [35mvar[m[m -> private/var

subprocess module has received several important changes in the last versions of Python 3.x. Prior to version 3.5 the high level function was subprocess.call(), subprocess.check_call() and subprocess.check_output() all this functionality was replaced by subprocess.run() from version 3.5 and beyond.

Module `multiprocessing`

Up to now, we have been dealing with serial processes but now most computers have several cores that allow us to do multiprocessing. Multiprocessing refers to the ability of a system to support more than one processor at the same time. Applications in a multiprocessing system are broken into smaller routines that run independently and in more cases, they talk to each other very infrequently. A simple way to see this is to have 4 different drivers that try to go from point A to point B. Each driver can take their own path but in the end, they will get together at point B. Python has different methods, where the operating system allocates these threads to the processors improving the performance of the system.

multiprocessing is a package that supports spawning processes using an API similar to the threading module. The multiprocessing package effectively side-stepping the Global Interpreter Lock by using subprocesses instead of threads. Due to this, the multiprocessing module allows the programmer to fully leverage multiple processors on a given machine.

For intensive numerical calculations, multiprocessing must be preferred over multithreading a similar module that spawns threads instead of processes.

The frequently use class Pool offers a simple way to spawn multiple workers to divide the same function over an iterable dividing the workload over several workers. The prototypical example is like this:

import sys
sys.path.insert(0, './scripts')

from worker import funcx2

import multiprocessing

multiprocessing.cpu_count()

import multiprocessing as mp

from worker import funcx2

with mp.Pool() as pool:
    args = list(range(10))
    res = pool.map(funcx2, args)
    pool.close()
    pool.join()

res

[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]

import multiprocessing

from worker import funcx2

def driver_func():
    PROCESSES = 4
    with multiprocessing.Pool(PROCESSES) as pool:
        params = [(1, ), (2, ), (3, ), (4, )]
        results = [pool.apply_async(funcx2, p) for p in params]

        for r in results:
            print('\t', r.get())
driver_func()

from multiprocessing import Pool

from worker import funcx2

if __name__ == '__main__':
    with Pool(4) as p:
        print(p.map(funcx2, [1, 2, 3]))

[1, 4, 9]

import math
import matplotlib.pyplot as plt

ppn=multiprocessing.cpu_count()
ppn=1

from worker import funcx2

if __name__ == '__main__':
    with multiprocessing.Pool(ppn) as p:
        ret = p.map(funcx2, range(1,100))
        
plt.plot(ret);

png

multiprocessing.cpu_count()

This is a function to get the number of cores on the system. That is different from the number of cores available to the Python process. The recommended method is using os.sched_getaffinity(0) but it is absent on some architectures. In particular in macOS, Windows, and some old Linux distros.

Final Remarks

The Python Standard Library is extensive, and the API is more prone to changes than the language itself. In real projects is better to decide what will be the oldest version of Python that will be supported and keep compatibility until the marker is shifted for a more recent version. Most Linux distributions today include Python 3.9 or newer.

Acknowledgments and References

Changes to the original tutorial include strict Python 3 formats and a split of the material to fit a series of lessons on Python Programming for WVU’s faculty and graduate students.

The support of the National Science Foundation and the US Department of Energy under projects: DMREF-NSF 1434897, NSF OAC-1740111 and DOE DE-SC0016176 is recognized.

Back of the Book

plt.figure(figsize=(3,3))
n = chapter_number
maxt=(2*(n-1)+3)*np.pi/2
t = np.linspace(np.pi/2, maxt, 1000)
tt= 1.0/(t+0.01)
x = (maxt-t)*np.cos(t)**3
y = t*np.sqrt(np.abs(np.cos(t))) + np.sin(0.3*t)*np.cos(2*t)
plt.plot(x, y, c="green")
plt.axis('off');

png

end = time.time()
print(f'Chapter {chapter_number} run in {int(end - start):d} seconds')

Chapter 2 run in 3 seconds

Key Points

Python is an easy-to-learn programming language.

Adjurn

Overview

Teaching: min
Exercises: min

Topics

Objectives

Key Points

Terminal-based Text Editors

Overview

Teaching: 60 min
Exercises: 30 min

Topics

How do I edit files with the terminal?

Objectives

Learn about three major editor in Linux/Unix: vim, emacs and nano

Learn the basic key combinations and operation of those editors

Terminal-based Text Editors

During your interaction with the cluster from the command line you need to deal with text files. As we learn from the previous episode, for just reading files, we can use the commands cat, more and less. For modifying text files we need a different application, a text editor. Notice that on the cluster we are working with pure text files in contrast with office applications like Microsoft Word and equivalent free versions like LibreOffice. Those applications are called “Word Processors” as they not only deal with the text content but they also are in charge of the control how the text is presented on screen and on paper. “Word Processors” are not the same as “Text Editors” and for most cases “Word Processors” are of no use in HPC clusters.

Text editors work just with the characters, spaces and new lines. When a file only contain those elements without any information about formatting, the file is said is in “Plain Text”. There is one important difference on how Windows and Linux/Linux marks new lines, making Windows “Text Files” as having some extra “spurious” characters at the end of each line and text files created on Linux as having no new lines at all when read with Windows applications like “Notepad”. To solve this situation, there are a couple of applications on Linux that convert from one “flavor” of text file into the other. They are “dos2unix” and “unix2dos”.

There are several terminal-based text editors available on Linux/Unix. From those we have selected three to present on this episode for you. They are nano, emacs, and vim. Your choice of an editor depends mostly on how much functionality do you want from your editor, how many fingers do you want to use for a given command, and the learning curve to master it. There is nothing wrong of using one of those editors over the others. Beginners of user who rarely edit files would find nano a pretty fine and simple editor for their needs that has basically no learning curve. If you advance deeper into the use of the cluster and edit files often your choice will be most likely one between emacs or vi/vim with the choice being mostly a matter of preference as both are full featured editors.

nano and emacs are direct input editors, ie you start writing directly as soon as you type with the keyboard. In contrast vi/vim is a modal editor. You type keys to change modes on the editor, some of these keys allowing you to start typing or return to command mode where new commands can be entered. In any case there are quite a large number of commands and key combinations that can be entered on any of those editors. For this episode we will concentrate our attention on a very specific set of skills that once learned will give you to work with text files. The skills are:

Open the editor to open a file, save the file that is being edited or saving the file and leaving the editor.
Move around the file being edited. Going to the beginning, the end or a specific line.
Copy, cut and paste text on the same file.
Search for a set of characters and use the search and replace functionality.

There is far more to learn in a text editor, each of those skills can be go deeper into more complex functionality and that is the major difference between nano and the other two editor, the later giving you far more complexity and power in the skills at the price of a steeper learning curve.

Meta, Alt and Option keys

On modern keyboards the Alt key has come to replace the Meta key of the old MIT keyboards. Both nano and emacs make extensive use of Meta for some key combinations. A situation that can be confusing on windows machines with Alt and Win keys and on Mac with the Option and Command keys.

Since the 1990s Alt has been printed on the Option key (⌥ Opt) on most Mac keyboards. Alt is used in non-Mac software, such as non-macOS Unix and Windows programs, but in macOS it is always referred as the Option key. The Option key’s behavior in macOS differs slightly from that of the Windows Alt key (it is used as a modifier rather than to access pull-down menus, for example).

On Macs Terminal application under the “Edit” > “Use Option as Meta key”. For emacs you can use ESC as a replacement of the Meta key.

Nano

Nano is a small andfriendly editor with commands that are generally accessed by using Control (Ctrl) combined with some other key.

Opening and closing the editor

You can start editing a file using a command line like this:

$ nano myfile.f90

To leave the editor type Ctrl+X, you will be asked if you want to save your file to disk. Another option is to save the file with Ctrl+O but remaing on the editor.

Moving around the file

On nano you can start typing as soon you open the file and the arrow keys will move you back and for on the same line or up and down on lines. For large files is always good to learn how to move to the begining and end of the file. Use Meta+\ and Meta+/ to do that. Those key combinations are also shown as M-\ (first line) M-/ (last line). To move to a specific line and column number use Ctrl+_, shown on the bottom bar as ^_

Copy, cut and paste

The use the internal capabilities of the text editor to copy and paste starts by selecting the area of text that you want to copy or cut. Use Meta+A to start selecting the area to copy use Meta+6 to delete use Meta+Delete, to cut but save the contents Ctrl+K to paste the contents of the region Ctrl+U

Search for text and search and Replace

To search use Ctrl+W, you can repeat the command to searching for more matches, to search and replace use Ctrl+\ enter the text to search and the text to replace in place.

Reference

Beyond the quick commands above, there are several commands available on nano, and the list below comes from the help text that you can see when execute Ctrl+G. When you see the symbol "\^", it means to press the Control Ctrl key; the symbol "M-" is called Meta, but in most keyboards is identified with the Alt key or Windows key. See above for the discussion about the use of Meta key.

^G  (F1)            Display this help text
^X  (F2)            Close the current file buffer / Exit from nano
^O  (F3)            Write the current file to disk
^J  (F4)            Justify the current paragraph

^R  (F5)            Insert another file into the current one
^W  (F6)            Search for a string or a regular expression
^Y  (F7)            Move to the previous screen
^V  (F8)            Move to the next screen

^K  (F9)            Cut the current line and store it in the cutbuffer
^U  (F10)           Uncut from the cutbuffer into the current line
^C  (F11)           Display the position of the cursor
^T  (F12)           Invoke the spell checker, if available

^_  (F13)   (M-G)   Go to line and column number
^\  (F14)   (M-R)   Replace a string or a regular expression
^^  (F15)   (M-A)   Mark text at the cursor position
    (F16)   (M-W)   Repeat last search

M-^         (M-6)   Copy the current line and store it in the cutbuffer
M-}                 Indent the current line
M-{                 Unindent the current line

^F                  Move forward one character
^B                  Move back one character
^Space              Move forward one word
M-Space             Move back one word
^P                  Move to the previous line
^N                  Move to the next line
^A                  Move to the beginning of the current line
^E                  Move to the end of the current line
M-(         (M-9)   Move to the beginning of the current paragraph
M-)         (M-0)   Move to the end of the current paragraph
M-\         (M-|)   Move to the first line of the file
M-/         (M-?)   Move to the last line of the file

M-]                 Move to the matching bracket
M--                 Scroll up one line without scrolling the cursor
M-+         (M-=)   Scroll down one line without scrolling the cursor

M-<         (M-,)   Switch to the previous file buffer
M->         (M-.)   Switch to the next file buffer

M-V                 Insert the next keystroke verbatim
^I                  Insert a tab at the cursor position
^M                  Insert a newline at the cursor position
^D                  Delete the character under the cursor
^H                  Delete the character to the left of the cursor
M-T                 Cut from the cursor position to the end of the file

M-J                 Justify the entire file
M-D                 Count the number of words, lines, and characters
^L                  Refresh (redraw) the current screen

M-X                 Help mode enable/disable
M-C                 Constant cursor position display enable/disable
M-O                 Use of one more line for editing enable/disable
M-S                 Smooth scrolling enable/disable
M-P                 Whitespace display enable/disable
M-Y                 Color syntax highlighting enable/disable

M-H                 Smart home key enable/disable
M-I                 Auto indent enable/disable
M-K                 Cut to end enable/disable
M-L                 Long line wrapping enable/disable
M-Q                 Conversion of typed tabs to spaces enable/disable

M-B                 Backup files enable/disable
M-F                 Multiple file buffers enable/disable
M-M                 Mouse support enable/disable
M-N                 No conversion from DOS/Mac format enable/disable
M-Z                 Suspension enable/disable

Emacs

Emacs is an extensible, customizable, open-source text editor. Together with vi/vim is one the most widely used editors in Linux/Unix environments. There are a big number of commands, customization and extra modules that can be integrated with Emacs. We will just briefly cover the basics as we did for nano

Opening and closing the editor

In addition to the terminal-base editor, emacs also has a GUI environment that could be selected by default. To ensure that you remain in terminal-based version use:

$ emacs -nw data.txt

To leave the editor execute Ctrl+X C, if you want to save the file to disk use Ctrl+X S, another representation of the keys to save and close could be C-x C-s C-x C-c, actually, the Ctrl key can be keep pressed while you hit the sequence x s x c to get the same effect.

Moving around the file

To go to the beginning of the file use Meta+< to the end of the file Meta+>. To go to a given line number use Ctrl+g Ctrl+g

Copy, cut and paste

To copy or cut regions of text starts by selecting the area of text that you want to copy or cut. Use Ctrl+Space to start selecting the area. To copy use Meta+W to delete use Ctrl+K, to cut but save the contents Ctrl+W. Finally, to paste the contents of the region Ctrl+Y

Search for text and search and Replace

To search use Ctrl+S, you can repeat the command to searching for more matchs, to search and replace use Meta+% enter the text to search and the text to replace in place.

Reference

The number of commands for Emacs is large, here the basic list of commands for editing, moving and searching text.

The best way of learning is keeping at hand a sheet of paper with the commands For example GNU Emacs Reference Card can show you most commands that you need.

Below you can see the same 2 page Reference Card as individual images.

Vi/Vim

The third editor is vi and found by default installed on Linux/Unix systems. The Single UNIX Specification and POSIX describe vi, so every conforming system must have it. A popular implementation of vi is vim that stands as an improved version. On our clusters we have vim installed.

Opening and closing the editor

You can open a file on vim with

$ vim code.py

vi is a modal editor: it operates in either insert mode (where typed text becomes part of the document) or normal mode (where keystrokes are interpreted as commands that control the edit session). For example, typing i while in normal mode switches the editor to insert mode, but typing i again at this point places an "i" character in the document. From insert mode, pressing ESC switches the editor back to normal mode. On the lines below we ask for pressing the ESC in case you are in insert mode to ensure you get back to normal mode

To leave the editor without saving type ESC follow by :q!. To leave the editor saving the file type ESC follow by :x To just save the file and continue editing type ESC follow by :w.

Moving around the file

On vim you can use the arrow keys to move around. In the traditional vi you have to use the following keys (on normal mode):

H Left
J Down
K Up
L Right

Go to the first line using ESC follow by :1. Go to the last line using ESC follow by :$.

Copy, cut and paste

To copy areas of text you start by entering in visual mode with v, selecting the area of interest and using d to delete, y to copy and p to paste.

Search for text and search and Replace

To search use / and the text you want to search, you can repeat the command to searching for more matches with n, to search and replace use :%s/<search pattern>/<replace text>/g enter the text to search and the text to replace everywhere. Use :%s/<search pattern>/<replace text>/gc to ask for confirmation before each modification.

Reference

A very beautiful Reference Card for vim can be found here: Vim CheatSheet

Exercise 1

Select an editor. The challenge is write this code in a file called Sierpinski.c
#include <stdio.h>

#define SIZE (1 << 5)
int main()
{
    int x, y, i;
    for (y = SIZE - 1; y >= 0; y--, putchar('\n')) {
        for (i = 0; i < y; i++) putchar(' ');
        for (x = 0; x + y < SIZE; x++)
            printf((x & y) ? "  " : "* ");
    }
    return 0;
}
For those using vi, here is the challenge. You cannot use the arrow keys. Not a single time! It is pretty hard if you are not used to it, but it is a good exercise to learn the commands.

Another interesting challenge is to write the line for (y = SIZE - 1; y >= 0; y--, putchar('\n')) and copy and paste it to > form the other 2 for loops in the code, and editing only after being copied.

Once you have successfully written the source code, you can see your hard work in action.

On the terminal screen, execute this:
$ gcc Sierpinski.c -o Sierpinski
This will compile your source code Sierpinski.c in C into a binary executable called Sierpinski. Execute the code with:
$ ./Sierpinski
The resulting output is kind of a surprise so I will not post it here. The original code comes from rosettacode.org

Exercise 2 (Needs X11)

On the folder workshops_hands-on/Introduction_HPC/4._Terminal-based_Editors you will find a Java code on file JuliaSet.java.

For this exercise you need to connect to the cluster with X11 support. On Thorny Flat that will be:
$ ssh -X <username>@ssh.wvu.edu
$ ssh -X <username>@tf.hpc.wvu.edu
Once you are there execute this command to load the Java compiler
$ module load lang/java/jdk1.8.0_201
Once you have loaded the module go to the folder workshops_hands-on/Introduction_HPC/4._Terminal-based_Editors and compile > the Java code with this command
$ javac JuliaSet.java
and execute the code with:
$ java JuliaSet
A window should pop up on your screen. Now, use one of the editors presented on this episode and do the changes mentioned on the source code to made the code > multithreaded. Repeat the same steps for compiling and executing the code.

Change a bit the parameters on the code, the size of the window for example or the constants CX and CY.

Exercise 3

On the folder workshops_hands-on/Introduction_HPC/4._Terminal-based_Editors there is a script download-covid19.sh. The script will download an updated compilation of Official Covid-19 cases around the world. Download the data about Covid 19 owid-covid-data.csv using the command:
$> sh download-covid19.sh
Open the file owid-covid-data.csv with your favorite editor. Go to to the first and last line on that file. The file has too many lines to be scrolled line by line.

Search for the line with the string United States,2021-06-30

Why vi was programmed to not use the arrow keys?

From Wikipedia with a anecdotal story from The register

Joy used a Lear Siegler ADM-3A terminal. On this terminal, the Escape key was at the location now occupied by the Tab key on the widely used IBM PC keyboard (on the left side of the alphabetic part of the keyboard, one row above the middle row). This made it a convenient choice for switching vi modes. Also, the keys h,j,k,l served double duty as cursor movement keys and were inscribed with arrows, which is why vi uses them in that way. The ADM-3A had no other cursor keys. Joy explained that the terse, single character commands and the ability to type ahead of the display were a result of the slow 300 baud modem he used when developing the software and that he wanted to be productive when the screen was painting slower than he could think.

Key Points

For editing files from the terminal there are several editor available

nano is an easy to use editor with commands that are shown on the bottom, good for beginners.

emacs is a full featured editor that relies on multiple key combinations to control its operation.

vi/vim is installed by default on every Linux system, it works by changing between ‘modes’

Software on HPC Clusters

Overview

Teaching: 60 min
Exercises: 30 min

Topics

What are the options to enable software packages on an HPC cluster?

What are the differences between environment modules, conda, and apptainer?

What are environment modules and how to use them?

How do I use and create conda environments?

How do I open a shell and execute commands on an Apptainer/Singularity container?

Objectives

Learn about the three main options to enable software on HPC clusters.

Load and unload environment modules

Activate and change conda environments

Get a shell and execute commands inside singularity containers.

Introduction

Many software packages are being executed on an HPC cluster daily. Each area of science uses its own set of software packages. Sometimes, the same software package is used in multiple versions, and those versions must be available on the same HPC cluster. To solve all these challenges, several options have been implemented on HPC clusters. The different options offer various levels of isolation from the host system, and some of these options are better suited for particular kinds of software.

Environment Modules

Environment modules are a mechanism that easily enables software by allowing administrators to install non-regular locations and the user to adapt his/her environment to access those locations and use the software installed there. By changing specific variables on the shell, different versions of packages can be made visible to the shell or to a script. Environment modules is a software package that gives the user the ability to change the variables that the shell uses to find executables and libraries. To better understand how environment modules do their job it is essential to understand the concept of variables in the shell and the particular role of special variables called environment variables

Shell variables and environment variables

The shell is a programming language in itself. As with any programming language, it has the ability to define placeholders for storing values. Those placeholders are called variables and the shell commands and shell scripts can be made use of them. Shell variables can be created on the shell using the operator =. For example:

$ A=10
$ B=20

Environment variables are shell variables that are exported, i.e., converted into global variables. The shell and many other command line programs use a set of variables to control their behavior. Those variables are called environment variables Think about them as placeholders for information stored within the system that passes data to programs launched in the shell.

To create an environment variable, you can first to create a variable and make it and environment variable using the command export followed by the name of the variable.

$ A=10
$ B=20
$ export A
$ export B

This procedure can be simplified with a single line that defines and export the variable. Example:

$ export A=10
$ export B=20

Environment Variables control CLI functionality. They declare where to search for executable commands, where to search for libraries, which language display messages to you, how you prompt looks. Beyond the shell itself, environment variables are use by many codes to control their own operation.

You can see all the variables currently defined by executing:

$ env

Environment variables are similar to the shell variables that you can create of the shell. Shell variables can be used to store data and manipulated during the life of the shell session. However, only environment variables are visible by child processes created from that shell. To clarify this consider this script:

#!/bin/bash

echo A= $A
echo B= $B
C=$(( $A + $B ))
echo C= $C

Now create two shell variables and execute the script, do the same with environment variables and notice that now the script is able to see the variables.

Some common environment variables commonly use by the shell are:

Environment Variable	Description
$USER	Your username
$HOME	The path to your home directory
$PS1	Your prompt
$PATH	List of locations to search for executable commands
$MANPATH	List of locations to search for manual pages
$LD_LIBRARY_PATH	List of locations to search for libraries in runtime
$LIBRARY_PATH	List of locations to search for libraries during compilation (actually during linking)

Those are just a few environment variables of common use. There are many more. Changing them will change where executables are found, which libraries are used and how the system behaves in general. That is why managing the environment variables properly is so important on a machine, and even more on a HPC cluster, a machine that runs many different codes with different versions.

Here is where environment modules enter.

Environment Modules

The modules software package allows you to dynamically modify your user environment by using modulefiles.

Each module file contains the information needed to configure the shell for an application. After the module’s software package is initialized, the environment can be modified on a per-module basis using the module command, which interprets module files. Typically, module files instruct the module command to alter or set shell environment variables such as PATH, MANPATH, and others. The module files can be shared by many users on a system, and users can have their own collection to supplement or replace the shared module files.

As a user, you can add and remove module files from the current environment. The environment changes contained in a module file can also be summarized through the module show command. You are welcome to change modules in your .bashrc or .cshrc, but be aware that some modules print information (to standard error) when loaded. This should be directed to a file or /dev/null when loaded in an initialization script.

Basic arguments

The following table lists the most common module command options.

Command	Description
module list	Lists modules currently loaded in a user’s environment.
module avail	Lists all available modules on a system.
module show	Shows environment changes that will be made by loading a given module.
module load	Loads a module.
module unload	Unloads a module.
module help	Shows help for a module.
module swap	Swaps a currently loaded module for an unloaded module.

Exercise: Using modulefiles
Check the modules that you currently have and clean (purge) your environment from them. Check again and confirm that no module is loaded.

Check which versions of Python, R, and GCC you have from the RHEL itself. Try to get and idea of how old those three components are. For python and R, all that you have to do is enter the corresponding command (R or python). For GCC you need to use gcc --version and see the date of those programs.
Now let’s get a newer version of those three components by loading the corresponding modules. Search for the module for Python 3.10.11, R 4.4.1, and GCC 9.3.0 and load the corresponding modules. To make things easier, you can use check the availability of modules just in the languages section.
module avail lang
module load lang/python/cpython_3.11.3_gcc122 lang/r/4.4.1_gcc122 lang/gcc/12.2.0 
Check again which version of those three components you have now. Notice that in the case of Python 3, the command python still goes towards the old Python 2.6.6, as the Python 3.x interpreter is not backward compatible with Python 2.x the new command is called python3. Check its version by entering the command.
~$ python3 --version
Clean all of the environment
~$ module purge
Go back and purge all the modules from your environment. We will now explore why it is essential to use a recent compiler. Try to compile the code at workshops_hands-on/Introduction_HPC/5._Environment_Modules/lambda_c++14.cpp. Go to the folder and execute:
~$ g++ lambda_c++14.cpp
At this point, you should have received a list of errors, that is because even if the code is C++ it uses elements of the language that were not present at that time on C++ Specification. The code actually uses C++14, and only recent versions of GCC allow for these declarations. Let’s check how many GCC compilers we have available on Thorny Flat.
~$ module avail lang/gcc
Now, from that list, start loading and trying to compile the code as indicated above. Which versions of GCC allow you to compile the code? Also try the Intel compilers. In the case of the Intel compiler, the command to compile the code is:
~$ icpc lambda_c++14.cpp
Try with all the Intel compilers. It will fail with some of them. That is because the default standard for the Intel C++ compiler is not C++14. You do not need to declare it explicitly, and for Intel Compiler Suite 2021, but for older versions, the correct command line is:
~$ icpc lambda_c++14.cpp -std=c++14
It should be clearer why modules are an important feature of any HPC infrastructure, as it allows you to use several compilers, libraries, and packages in different versions. On a normal computer, you usually have just one.

Conda

Conda is an open-source package management system and environment management system. Conda quickly installs, runs, and updates packages and their dependencies. Conda easily creates, saves, loads, and switches between environments. It was created for Python programs, but it can package and distribute software for any language.

Conda, as a package manager, helps you find and install packages. If you need a package that requires a different version of Python, you do not need to switch to a different environment manager because conda is also an environment manager. With just a few commands, you can set up a totally separate environment to run that different version of Python while continuing to run your usual version of Python in your normal environment.

There are two installers for conda, Anaconda and Miniconda.

Anaconda vs Miniconda

Anaconda is a downloadable, free, open-source, high-performance, and optimized Python and R distribution. Anaconda includes conda, conda-build, Python, and 100+ automatically installed, open-source scientific packages and their dependencies that have been tested to work well together, including SciPy, NumPy, and many others. Ananconda is more suited to be installed on a desktop environment as you get, after installation, a fairly complete environment for scientific computing.

On the other hand, Miniconda is a minimalistic installer for conda. Miniconda is a small, bootstrap version of Anaconda that includes only conda, Python, the packages they depend on, and a small number of other useful packages, including pip, zlib, and a few others. Miniconda is more suited for HPC environments where a minimal installation is all that is needed, and users can create their own environments as needed.

Activating Conda on Thorny Flat and Dolly Sods

On Thorny Flat, the command to activate conda is:

~$ source /shared/software/conda/conda_init.sh

Or you can see the command line trying to load the module for conda

~$ module load conda

After activation, you are positioned in the base environment.

When you have activated conda, you are always inside a conda environment. Initially, you start on the base environment, and your prompt in the shell will include a prefix in parentheses indicating the name of the conda environment you are currently using.

Conda Environments

Conda allows you to change your environment easily. It also gives you tools to create new environments, change from one environment to another, and install packages and their dependencies. Conda environments will not interact with other environments, so you can easily keep different versions of packages just by creating multiple conda environments and populating those with the various versions of software you want to use.

When you begin using conda, you already have a default environment named base. You cannot install packages on the base environment as that is a centrally managed environment. You can, however, create new environments for installing packages. Try to keep separate environments for different packages or groups of packages. That reduces the chances of incompatibility between them.

Knowing which environments are available

At the time of this tutorial (2024), Thorny Flat offers the following environments centrally installed::

$> conda env list

(base) trcis001:~$ conda env list
# conda environments:
#
base                    * /shared/software/conda
abienv_py36               /shared/software/conda/envs/abienv_py36
abienv_py37               /shared/software/conda/envs/abienv_py37
cutadaptenv               /shared/software/conda/envs/cutadaptenv
genomics_2024             /shared/software/conda/envs/genomics_2024
materials_2024            /shared/software/conda/envs/materials_2024
materials_2024_gcc93      /shared/software/conda/envs/materials_2024_gcc93
materials_discovery       /shared/software/conda/envs/materials_discovery
moose                     /shared/software/conda/envs/moose
neural_gpu                /shared/software/conda/envs/neural_gpu
picrust                   /shared/software/conda/envs/picrust
picrust2                  /shared/software/conda/envs/picrust2
python27                  /shared/software/conda/envs/python27
python35                  /shared/software/conda/envs/python35
python36                  /shared/software/conda/envs/python36
python37                  /shared/software/conda/envs/python37
qiime2-2022.8             /shared/software/conda/envs/qiime2-2022.8
qiime2-2023.2             /shared/software/conda/envs/qiime2-2023.2
qiime2-amplicon-2023.9    /shared/software/conda/envs/qiime2-amplicon-2023.9
qiime2-shotgun-2023.9     /shared/software/conda/envs/qiime2-shotgun-2023.9
qiime2-tiny-2023.9        /shared/software/conda/envs/qiime2-tiny-2023.9
r_4.2                     /shared/software/conda/envs/r_4.2
scipoptsuite              /shared/software/conda/envs/scipoptsuite
sourcetracker2            /shared/software/conda/envs/sourcetracker2
st2_py36                  /shared/software/conda/envs/st2_py36
st2_py37                  /shared/software/conda/envs/st2_py37
tensorflow18-py36         /shared/software/conda/envs/tensorflow18-py36

Activating an existing environment

Suppose that you want to use the environment called “tpd0001”. To activate this environment, execute::

conda activate tpd0001

Deactivating the current environment

The current environment can be deactivated with::

conda deactivate

If you are in the base environment, the deactivation will not have any effect. You are always at least in the base environment.

Create a new environment

We will name the environment snowflakes and install the package BioPython. At the Anaconda Prompt or in your terminal window, type the following::

(base) trcis001:~$ conda create --name snowflakes
Retrieving notices: ...working... done
Channels:
 - https://conda.software.inl.gov/public
 - conda-forge
Platform: linux-64
Collecting package metadata (repodata.json): done
Solving environment: done

## Package Plan ##

  environment location: /users/gufranco/.conda/envs/snowflakes



Proceed ([y]/n)? y

Preparing transaction: done
Verifying transaction: done
Executing transaction: done
#
# To activate this environment, use
#
#     $ conda activate snowflakes
#
# To deactivate an active environment, use
#
#     $ conda deactivate

From here you can activate your environment and install the packages of your willing.

(base) trcis001:~$ conda activate snowflakes
(snowflakes) trcis001:~$

or if you want also to install a package you can execute::

conda create --name snowflakes -c bioconda biopython

Conda collects metadata about the package and its dependencies and produces an installation plan::

Channels:
 - bioconda
 - https://conda.software.inl.gov/public
 - conda-forge
Platform: linux-64
Collecting package metadata (repodata.json): done
Solving environment: done

## Package Plan ##

  environment location: /users/gufranco/.conda/envs/snowflakes

  added / updated specs:
    - biopython


The following packages will be downloaded:

    package                    |            build
    ---------------------------|-----------------
    biopython-1.70             |      np112py36_1         2.6 MB  bioconda
    ca-certificates-2024.7.4   |       hbcca054_0         151 KB  conda-forge
    ld_impl_linux-64-2.40      |       hf3520f5_7         691 KB  conda-forge
    libgcc-ng-14.1.0           |       h77fa898_0         822 KB  conda-forge
    libgomp-14.1.0             |       h77fa898_0         446 KB  conda-forge
    libpng-1.6.43              |       h2797004_0         281 KB  conda-forge
    libsqlite-3.46.0           |       hde9e2c9_0         845 KB  conda-forge
    libstdcxx-ng-14.1.0        |       hc0a3c3a_0         3.7 MB  conda-forge
    libwebp-base-1.4.0         |       hd590300_0         429 KB  conda-forge
    libzlib-1.2.13             |       h4ab18f5_6          60 KB  conda-forge
    mmtf-python-1.1.3          |     pyhd8ed1ab_0          25 KB  conda-forge
    ncurses-6.5                |       h59595ed_0         867 KB  conda-forge
    numpy-1.12.1               |py36_blas_openblash1522bff_1001         3.8 MB  conda-forge
    reportlab-3.5.68           |   py36h3e18861_0         2.4 MB  conda-forge
    sqlite-3.46.0              |       h6d4b2fc_0         840 KB  conda-forge
    zlib-1.2.13                |       h4ab18f5_6          91 KB  conda-forge
    zstd-1.5.6                 |       ha6fb4c9_0         542 KB  conda-forge
    ------------------------------------------------------------
                                           Total:        18.5 MB

The following NEW packages will be INSTALLED:

  _libgcc_mutex      conda-forge/linux-64::_libgcc_mutex-0.1-conda_forge 
  _openmp_mutex      conda-forge/linux-64::_openmp_mutex-4.5-2_gnu 
  biopython          bioconda/linux-64::biopython-1.70-np112py36_1 
  blas               conda-forge/linux-64::blas-1.1-openblas 
  ca-certificates    conda-forge/linux-64::ca-certificates-2024.7.4-hbcca054_0 
  freetype           conda-forge/linux-64::freetype-2.12.1-h267a509_2 
  jpeg               conda-forge/linux-64::jpeg-9e-h0b41bf4_3 
  lcms2              conda-forge/linux-64::lcms2-2.12-hddcbb42_0 
  ld_impl_linux-64   conda-forge/linux-64::ld_impl_linux-64-2.40-hf3520f5_7 
  lerc               conda-forge/linux-64::lerc-3.0-h9c3ff4c_0 
  libdeflate         conda-forge/linux-64::libdeflate-1.10-h7f98852_0 
  libffi             conda-forge/linux-64::libffi-3.4.2-h7f98852_5 
  libgcc-ng          conda-forge/linux-64::libgcc-ng-14.1.0-h77fa898_0 
  libgfortran-ng     conda-forge/linux-64::libgfortran-ng-7.5.0-h14aa051_20 
  libgfortran4       conda-forge/linux-64::libgfortran4-7.5.0-h14aa051_20 
  libgomp            conda-forge/linux-64::libgomp-14.1.0-h77fa898_0 
  libnsl             conda-forge/linux-64::libnsl-2.0.1-hd590300_0 
  libpng             conda-forge/linux-64::libpng-1.6.43-h2797004_0 
  libsqlite          conda-forge/linux-64::libsqlite-3.46.0-hde9e2c9_0 
  libstdcxx-ng       conda-forge/linux-64::libstdcxx-ng-14.1.0-hc0a3c3a_0 
  libtiff            conda-forge/linux-64::libtiff-4.3.0-h0fcbabc_4 
  libwebp-base       conda-forge/linux-64::libwebp-base-1.4.0-hd590300_0 
  libzlib            conda-forge/linux-64::libzlib-1.2.13-h4ab18f5_6 
  mmtf-python        conda-forge/noarch::mmtf-python-1.1.3-pyhd8ed1ab_0 
  msgpack-python     conda-forge/linux-64::msgpack-python-1.0.2-py36h605e78d_1 
  ncurses            conda-forge/linux-64::ncurses-6.5-h59595ed_0 
  numpy              conda-forge/linux-64::numpy-1.12.1-py36_blas_openblash1522bff_1001 
  olefile            conda-forge/noarch::olefile-0.46-pyh9f0ad1d_1 
  openblas           conda-forge/linux-64::openblas-0.3.3-h9ac9557_1001 
  openjpeg           conda-forge/linux-64::openjpeg-2.5.0-h7d73246_0 
  openssl            conda-forge/linux-64::openssl-1.1.1w-hd590300_0 
  pillow             conda-forge/linux-64::pillow-8.3.2-py36h676a545_0 
  pip                conda-forge/noarch::pip-21.3.1-pyhd8ed1ab_0 
  python             conda-forge/linux-64::python-3.6.15-hb7a2778_0_cpython 
  python_abi         conda-forge/linux-64::python_abi-3.6-2_cp36m 
  readline           conda-forge/linux-64::readline-8.2-h8228510_1 
  reportlab          conda-forge/linux-64::reportlab-3.5.68-py36h3e18861_0 
  setuptools         conda-forge/linux-64::setuptools-58.0.4-py36h5fab9bb_2 
  sqlite             conda-forge/linux-64::sqlite-3.46.0-h6d4b2fc_0 
  tk                 conda-forge/linux-64::tk-8.6.13-noxft_h4845f30_101 
  wheel              conda-forge/noarch::wheel-0.37.1-pyhd8ed1ab_0 
  xz                 conda-forge/linux-64::xz-5.2.6-h166bdaf_0 
  zlib               conda-forge/linux-64::zlib-1.2.13-h4ab18f5_6 
  zstd               conda-forge/linux-64::zstd-1.5.6-ha6fb4c9_0 


Proceed ([y]/n)? 

Conda asks if you want to proceed with the plan::

Proceed ([y]/n)? y
Type "y" and press Enter to proceed.

After that, conda, download, and install the packages, creating a new environment for you. The final message shows how to activate and deactivate the environment::

Preparing transaction: done
Verifying transaction: done
Executing transaction: done
#
# To activate this environment, use
#
#     $ conda activate snowflakes
#
# To deactivate an active environment, use
#
#     $ conda deactivate

Each environment is isolated from other conda environments, and that allows you to keep several environments with different packages on them or different versions of the same packages. As the message shows, you activate the environment with::

conda activate snowflakes

Notice that when you activate a new environment, the prompt changes, adding a prefix in parenthesis to indicate which conda environment you are using at that moment. To check the environments available, execute::

conda env list

or::

conda info --envs

Conda and Python

When you create a new environment, conda installs the same Python version used to install conda on Thorny Flat (3.9). If you want to use a different version of Python, for example, Python 2.7, create a new environment and specify the version of Python that you want::

conda create --name python27 python=2.7

You activate the environment::

conda activate python27

And verify the Python version::

$ python --version
Python 2.7.16 :: Anaconda, Inc.

Conda has packages for versions of python for 2.7, 3.5, 3.6 and 3.7

Managing packages and channels

New packages can be installed to existing conda environments. First search for packages with::

conda search mkl

Packages are stored in repositories called channels. By default, conda search on the pkgs/main channel only. However, there are many other packages on several other channels.

The most prominent channels to search for packages are intel, conda-forge and bioconda To search for packages there execute::

conda search -c intel mkl

conda search -c conda-forge nitime

conda search -c bioconda blast

Packages can be installed on the current environment with::

conda install -c conda-forge nitime

In this case conda will pick the most recent version of the package compatible with the packages already present on the current environment. You can also be very selective on version and build that you want for the package. First get the list of versions and builds for the package that you want::

  $ conda search -c intel mkl
  Loading channels: done
  # Name                       Version           Build  Channel
  mkl                         2017.0.3         intel_6  intel
  mkl                         2017.0.4      h4c4d0af_0  pkgs/main
  mkl                         2018.0.0      hb491cac_4  pkgs/main
  mkl                         2018.0.0         intel_4  intel
  mkl                         2018.0.1      h19d6760_4  pkgs/main
  mkl                         2018.0.1         intel_4  intel
  mkl                         2018.0.2               1  pkgs/main
  mkl                         2018.0.2         intel_1  intel
  mkl                         2018.0.3               1  pkgs/main
  mkl                         2018.0.3         intel_1  intel
  mkl                           2019.0             117  pkgs/main
  mkl                           2019.0             118  pkgs/main
  mkl                           2019.0       intel_117  intel
  mkl                           2019.1             144  pkgs/main
  mkl                           2019.1       intel_144  intel
  mkl                           2019.2       intel_187  intel
  mkl                           2019.3             199  pkgs/main
  mkl                           2019.3       intel_199  intel
  mkl                           2019.4             243  pkgs/main
  mkl                           2019.4       intel_243  intel
  mkl                           2019.5       intel_281  intel

Now, install the package declaring the version and build::

$ conda install -c intel mkl=2019.4=intel_243
Collecting package metadata (current_repodata.json): done
Solving environment: done

## Package Plan ##

  environment location: /users/gufranco/.conda/envs/test

  added / updated specs:
    - mkl==2019.4=intel_243


The following packages will be downloaded:

    package                    |            build
    ---------------------------|-----------------
    intel-openmp-2019.5        |        intel_281         888 KB  intel
    mkl-2019.4                 |        intel_243       204.1 MB  intel
    tbb-2019.8                 |        intel_281         874 KB  intel
    ------------------------------------------------------------
                                           Total:       205.8 MB

The following NEW packages will be INSTALLED:

  intel-openmp       intel/linux-64::intel-openmp-2019.5-intel_281
  mkl                intel/linux-64::mkl-2019.4-intel_243
  tbb                intel/linux-64::tbb-2019.8-intel_281


Proceed ([y]/n)?


Downloading and Extracting Packages
tbb-2019.8           | 874 KB    | #################################################################################################################################### | 100%
mkl-2019.4           | 204.1 MB  | #################################################################################################################################### | 100%
intel-openmp-2019.5  | 888 KB    | #################################################################################################################################### | 100%
Preparing transaction: done
Verifying transaction: done
Executing transaction: done

Creating a new environment from a YML file

You can create your own environment, one easy way of doing that is via a YML file that describes the channels and packages that you want on your environment. The YML file will look like this, for a simple case when you want one env for bowtie2 (bowtie2.yml)

    name: thorny-bowtie2
    channels:
      - bioconda
      - conda-forge
      - defaults
    dependencies:
      - bowtie2

Another example is this YML file for installing a curated set of basic genomics codes that requires just a few dependencies. (biocore.yml)

name: biocode
channels:
  - bioconda
  - conda-forge
  - defaults
dependencies:
  - bamtools
  - bcftools
  - bedtools
  - hmmer
  - muscle
  - raxml
  - samtools
  - sga
  - soapdenovo-trans
  - soapdenovo2
  - sra-tools
  - vcftools
  - velvet

To create an environment from those YML files you can select one location on your scratch folder

conda env create -p $SCRATCH/bowtie2 -f bowtie2.yml

or for the biocore.yml

conda env create -p $SCRATCH/biocore -f biocore.yml

By default, new environments are created inside your $HOME folder on $HOME/.conda

Listing the packages inside one environment

Bowtie2 has a number of dependencies (19 dependencies for 1 package) Notice that only bowtie2 comes from bioconda channel. All other packages are part of conda-forge, a lower level channel.

$ conda activate $SCRATCH/bowtie2
$ conda list
# packages in environment at /scratch/gufranco/bowtie2:
#
# Name                    Version                   Build  Channel
bowtie2                   2.3.4.2          py36h2d50403_0    bioconda
bzip2                     1.0.6                h470a237_2    conda-forge
ca-certificates           2018.8.24            ha4d7672_0    conda-forge
certifi                   2018.8.24                py36_1    conda-forge
libffi                    3.2.1                hfc679d8_5    conda-forge
libgcc-ng                 7.2.0                hdf63c60_3    conda-forge
libstdcxx-ng              7.2.0                hdf63c60_3    conda-forge
ncurses                   6.1                  hfc679d8_1    conda-forge
openssl                   1.0.2p               h470a237_0    conda-forge
perl                      5.26.2               h470a237_0    conda-forge
pip                       18.0                     py36_1    conda-forge
python                    3.6.6                h5001a0f_0    conda-forge
readline                  7.0                  haf1bffa_1    conda-forge
setuptools                40.2.0                   py36_0    conda-forge
sqlite                    3.24.0               h2f33b56_1    conda-forge
tk                        8.6.8                         0    conda-forge
wheel                     0.31.1                   py36_1    conda-forge
xz                        5.2.4                h470a237_1    conda-forge
zlib                      1.2.11               h470a237_3    conda-forge

Using a conda environment in a submission script

To execute software in a non-interactive job you need to source the main script, activate the environment that contains the software you need, execute the the scientific code and deactivate the environment. This is a simple example showing that for bowtie2

#!/bin/bash

#SBATCH -J CONDA_JOB
#SBATCH -N 1
#SBATCH -c 4
#SBATCH -p standby
#SBATCH -t 4:00:00

source /shared/software/conda/conda_init.sh
conda activate $SCRATCH/bowtie2

bowtie2 .....

conda deactivate

Deleting an environment

You can execute this command to remove an environment you own.

conda remove --all -p $SCRATCH/bowtie2

conda env remove -n bowtie2

If the environment is named.

Downloading Miniconda

You do not need to install Miniconda on Thorny Flat or Dolly Sods. However, nothing prevents you from having your version of it if you want. Miniconda can be downloaded from::

wget https://repo.continuum.io/miniconda/Miniconda3-latest-Linux-x86_64.sh
sh Miniconda3-latest-Linux-x86_64.sh

No installing anything

Just load the module::

module purge
module load genomics/qiime

This module will load Python 2.7.3 and qiime on top of that. Conda is a particularly good option to install older packages that could still be available on channels like conda-forge and bioconda.

Singularity Containers

Containers are a software technology that allows us to keep control of the environment where a given code runs. Consider for example that you want to run a code in such a way the same code runs on several machines or clusters, ensuring that the same libraries are loaded and the same general environment is present. Different clusters could come installed with different compilers, different Linux distributions and different libraries in general. Containers can be used to package entire scientific workflows, software and libraries, and even data and move them to several compute infrastructures with complete reproducibility.

Containers are similar to Virtual Machines, however, the differences are enough to consider them different technologies and those differences are very important for HPC. Virtual Machines take up a lot of system resources. Each Virtual Machine (VM) runs not just a full copy of an operating system, but a virtual copy of all the hardware that the operating system needs to run. This quickly adds up to a lot of precious RAM and CPU cycles, valuable resources for HPC.

In contrast, all that a container requires is enough of an operating system, supporting programs and libraries, and system resources to run a specific program. From the user perspective, a container is in most cases a single file that contains the file system, ie a rather complete Unix filesystem tree with all libraries, executables, and data that are needed for a given workflow or scientific computation.

There are several container solutions, the most popular probably is Docker, however, the main issue with using docker on HPC is security, despite the name, containers do not actually contain the powers of the user who executes code on them. That is why you do not see Docker installed on an HPC cluster. Using dockers requires superuser access something that on shared resources like an HPC cluster is not typically possible.

Singularity offers an alternative solution to Docker, users can run the prepared images that we are offering on our clusters or bring their own.

For more information about Singularity and complete documentation see: https://singularity.lbl.gov/quickstart

How to use a singularity Image

There are basically two scenarios, interactive execution and job submission.

Interactive Job

If you are using Visit or RStudio, programs that uses the X11 forwarding, ensure to connect first to the cluster with X11 forwarding, before asking for an interactive job. In order to connect into Thorny with X11 forwarding use:

ssh -X <username>@ssh.wvu.edu

ssh -X <username>@tf.hpc.wvu.edu

Once you have login into the cluster, create an interactive job with the following command line, in this case we are using standby as queue but any other queue is valid.

salloc -c 4 -p standby

Once you get inside a compute node, load the module:

module load singularity

After loading the module the command singularity is available for usage, and you can get a shell inside the image with:

singularity shell /shared/containers/<Image Name>

Job Submission

In this case you do not need to export X11, just login into Thorny Flat

ssh <username>@ssh.wvu.edu

ssh <username>@tf.hpc.wvu.edu

Once you have login into the cluster, create a submission script (“runjob.pbs” for this example), in this case we are using standby as queue but any other queue is valid.

#!/bin/sh

#SBATCH -J SINGULARITY_JOB
#SBATCH -N 1
#SBATCH -c 4
#SBATCH -p standby
#SBATCH -t 4:00:00

module load singularity

singularity exec /shared/containers/<Image Name> <command_or_script_to_run>

Submit your job with

sbatch runjob.pbs

Exercise 1: Using singularity on the cluster (Interactive)

This exercise propose the use of singularity to access RStudio-server version 2023.12.1-402 and R 4.4.1

Follow the instructions for accessing an interactive session

The image is located at:
/shared/containers/RStudio-server-2023.12.1-402_R-4.4.1_jammy.sif 
Be sure that you can execute basic R commands. You can get an error message like:

WARNING: You are configured to use the CRAN mirror at https://cran.rstudio.com/. This mirror supports secure (HTTPS) downloads however your system is unable to communicate securely with the server (possibly due to out of date certificate files on your system). Falling back to using insecure URL for this mirror.

That is normal and due to the fact that compute nodes have no Internet access.

Exercise 2: Using singularity on the cluster (Non-interactive)

Create a script that reads a CSV with official statistics of population for US. The file can be downloaded from:
$ wget https://www2.census.gov/programs-surveys/popest/datasets/2010-2018/state/detail/SCPRC-EST2018-18+POP-RES.csv
However, the file is also present in the repository for hands-ons
$ git clone https://github.com/WVUHPC/workshops_hands-on.git
The folder is workshops_hands-on/Introduction_HPC/11._Software_Containers_Singularity. If you are not familiar with R programming, the script is there too. Notice that you cannot write your script to download the CSV file directly from the Census Bureau as the compute nodes have no Internet access. Write a submission script and submit.

Advanced topics

Modules: Creating a private repository

The basic procedure is to locate modules on a folder accessible by relevant users and add the variable MODULEPATH to your .bashrc

MODULEPATH controls the path that the module command searches when looking for modulefiles. Typically, it is set to a default value by the bootstrap procedure. MODULEPATH can be set using ’module use’ or by the module initialization script to search group or personal modulefile directories before or after the master modulefile directory.

Singularity: Creating your own images

You can create your own Singularity images and use them on our clusters. The only constrain is that images can only be created on your own machine as you need root access to create them.

The procedure that we will show will be executed on a remote machine provided by JetStream, it should the same if you have your own Linux machine and you have superuser access to it.

The creation of images is an interactive procedure. You learn how to put pieces together and little by little you build your own recipe for your image.

Lets start with a very clean image with centos.

The minimal recipe will bring an image from Docker with the latest version of CentOS. Lets call the file centos.bst

# Singularity container with centos
#
# This is the Bootstrap file to recreate the image.
#

Bootstrap: docker
From: centos:latest

%runscript
exec echo "The runscript is the containers default runtime command!"

%files

%environment

%labels
AUTHOR username@mail.wvu.edu

%post
echo "The post section is where you can install, and configure your container."
mkdir -p /data/bin
mkdir -p /gpfs
mkdir -p /users
mkdir -p /group
mkdir -p /scratch
touch /usr/bin/nvidia-smi

A few folders are created that help us to link special folders like /users, /scratch to the host file system. Other than that the image contains a very small but usable Linux CentOS machine.

We start with a writable sandboxed version, the exact command varies from machine to machine, but assuming that you can do sudo and the command singularity is available for root execute this:

sudo singularity build --sandbox centos centos.bst

Using container recipe deffile: centos.bst
Sanitizing environment
Adding base Singularity environment to container
Docker image path: index.docker.io/library/centos:latest
Cache folder set to /root/.singularity/docker
Exploding layer: sha256:8ba884070f611d31cb2c42eddb691319dc9facf5e0ec67672fcfa135181ab3df.tar.gz
Exploding layer: sha256:306a59f4aef08d54a38e1747ff77fc446103a3ee3aea83676db59d6d625b02a1.tar.gz
User defined %runscript found! Taking priority.
Adding files to container
Adding environment to container
Running post scriptlet
+ echo 'The post section is where you can install, and configure your container.'
The post section is where you can install, and configure your container.
+ mkdir -p /data/bin
+ mkdir -p /gpfs
+ mkdir -p /users
+ mkdir -p /group
+ mkdir -p /scratch
+ touch /usr/bin/nvidia-smi
Adding deffile section labels to container
Adding runscript
Finalizing Singularity container
Calculating final size for metadata...
Skipping checks
Singularity container built: centos
Cleaning up...

The result will be a folder called centos. We can enter into that folder to learn what we need to install the packages for our image.

sudo singularity shell --writable centos

For our exercise lets imagine that we want to use a package that opens a window. In particular, we now that we need a package that is called libgraph to get access to the graphics capabilities. The software is not provided by CentOS itself, so we need to compile it. We need to download, compile and install this package. We learn first how to do it and add that learning to the Bootstrap recipe file.

We need:

Download http://www.mirrorservice.org/sites/download.savannah.gnu.org/releases/libgraph/libgraph-1.0.2.tar.gz, so we need wget for that. This is one package that we need to install from yum.
We need compilers, and make. So we have to install gcc, gcc-c++ and make
The next time to try, you notice that you will also need some extra packages provided by EPEL, devel packages from CentOS and EPEL repositories. The packages are SDL-devel epel-release SDL_image-devel compat-guile18-devel and guile-devel.

Trial and error move you from the original recipe to this one (centos-libgraph.bst):

# Singularity container with centos
#
# This is the Bootstrap file to recreate the image.
#

Bootstrap: docker
From: centos:latest

%runscript
exec echo "The runscript is the containers default runtime command!"

%files

%environment

%labels
AUTHOR username@mail.wvu.edu

%post
echo "The post section is where you can install, and configure your container."

yum -y install wget make gcc gcc-c++ SDL-devel epel-release
yum -y update && yum -y install SDL_image-devel compat-guile18-devel guile-devel

mkdir -p /data/bin
mkdir -p /gpfs
mkdir -p /users
mkdir -p /group
mkdir -p /scratch
touch /usr/bin/nvidia-smi

cd /data
wget http://www.mirrorservice.org/sites/download.savannah.gnu.org/releases/libgraph/libgraph-1.0.2.tar.gz
tar -zxvf libgraph-1.0.2.tar.gz
cd libgraph-1.0.2 && ./configure --prefix=/data && make && make install

Notice that we have added a few lines using yum to install some packages, we add EPEL on the first line and we use it to install some extra packages on the second line.

yum -y install wget make gcc gcc-c++ SDL-devel epel-release
yum -y update && yum -y install SDL_image-devel compat-guile18-devel guile-devel

Finally, we use wget to get the sources and build libgraph. In order to save space on the VM, lets delete the old folder and create a new one with the new recipe.

sudo rm -rf centos
sudo singularity build --sandbox centos centos-libgraph.bst

The command takes longer and at the end you get libgraph installed at /data The final step will be use that to test that we are able to use libgraph with our application. The application is a couple of very small codes that use libgraph as dependency.

To achieve this we need.

Modify the environment variables PATH and LD_LIBRARY_PATH to point to the locations where libgraph and our binaries will be located.
Copy the sources circles.c and julia.c to the image and compile it.

The final version of the Bootstrap recipe looks like this centos-final.bst

# Singularity container with centos
#
# This is the Bootstrap file to recreate the image.
#

Bootstrap: docker
From: centos:latest

%runscript
exec echo "The runscript is the containers default runtime command!"

%files
julia.c
circles.c
sample.c

%environment
SHELL=/bin/bash
export SHELL
PATH=/data/bin:$PATH
export PATH
LD_LIBRARY_PATH=$LD_LIBRARY_PATH:/data/lib
export LD_LIBRARY_PATH

%labels
AUTHOR username@mail.wvu.edu

%post
echo "The post section is where you can install, and configure your container."
yum -y install wget make gcc gcc-c++ SDL-devel epel-release
yum -y update && yum -y install SDL_image-devel compat-guile18-devel guile-devel
mkdir -p /data/bin
mkdir -p /gpfs
mkdir -p /users
mkdir -p /group
mkdir -p /scratch
touch /usr/bin/nvidia-smi

mv /circles.c /julia.c /sample.c /data

cd /data
wget http://www.mirrorservice.org/sites/download.savannah.gnu.org/releases/libgraph/libgraph-1.0.2.tar.gz
tar -zxvf libgraph-1.0.2.tar.gz
cd libgraph-1.0.2 && ./configure --prefix=/data && make && make install

cd /data
gcc julia.c -o bin/julia -I/data/include -L/data/lib -lgraph -lm
gcc circles.c -o bin/circles -I/data/include -L/data/lib -lgraph -lm
gcc sample.c -o bin/sample -I/data/include -L/data/lib -lgraph -lm

We add a few sample files sample.c, circles.c and julia.c that uses the old graphics.h provided by libgraph.

The binaries are sample, cicles and julia and they are accessible on the command line.

When you have crafted a good recipe with the codes and data that you need. The last step is to create a final image. The command for that is below, remembering of deleting the centos folder to save space.

sudo rm -rf centos
sudo singularity build centos-final.simg centos-final.bst

This is the final image. It is not too big, it contains the packages that we installed from yum, the sources and binaries for libgraph and the sources for the couple of example sources that uses libgraph. The image can be move to any machine with singularity and should be able to run the codes.

Remember that to see the windows you should have and Xserver running on your machine and X11 forwarding on your ssh client.

Key Points

Modules. Use module avail to know all the modules on the cluster.

Modules. Use module load <module_name> to load a module.

Conda. Use conda env list to list the available environments.

Conda. Use conda activate to activate a conda environment.

Singularity. Use singularity shell <container> to get a shell inside the container.

Singularity. Use singularity exec <container> <command> to execute a command or script inside the container.

Adjurn

Overview

Teaching: min
Exercises: min

Topics

Objectives

Key Points

Python Scripting for HPC

Overview

Teaching: 45 min
Exercises: 15 min

Topics

How to use numpy to manipulate multidimensional arrays in Python?

How I split and select portions of a numpy array?

Objectives

Learn to create, manipulate, and slice numpy arrays

Python Programming for Scientists in a hurry

Chapter 4. NumPy

Guillermo Avendaño Franco
Aldo Humberto Romero

List of Notebooks

Python is a great general-purpose programming language on its own.
Python is a general purpose programming language. It is interpreted and dynamically typed and is very suited for interactive work and quick prototyping while being powerful enough to write large applications in. The lesson is particularly oriented to Scientific Computing. Other episodes in the series include:

Language Syntax
Standard Library
Scientific Packages
NumPy [This notebook]
Matplotlib
SciPy
Pandas
Cython
Parallel Computing

Setup

%load_ext watermark

%watermark

Last updated: 2024-07-26T13:26:24.085806-04:00

Python implementation: CPython
Python version       : 3.11.7
IPython version      : 8.14.0

Compiler    : Clang 12.0.0 (clang-1200.0.32.29)
OS          : Darwin
Release     : 20.6.0
Machine     : x86_64
Processor   : i386
CPU cores   : 8
Architecture: 64bit

import time
start = time.time()
chapter_number = 4
import matplotlib
%matplotlib inline
%load_ext autoreload
%autoreload 2

import numpy as np
import matplotlib.pyplot as plt

%watermark -iv

numpy     : 1.26.2
matplotlib: 3.8.2

NumPy: Multidimensional Arrays

Introduction
Array creation
Array Indexing, Sliding and Striding
Creating arrays from a file
Array data types
Universal functions
Copies and Views
Functional Programming
Broadcasting
More about NumPy

Introduction

NumPy is a Python library that provides a multidimensional array object, various derived objects (such as masked arrays and matrices), and an assortment of routines for fast operations on arrays.

NumPy is the core library for scientific computing in Python. It provides a high-performance multidimensional array object and tools for working with these arrays.

The main characteristics of NumPy for Scientific Computation are:

NumPy is written in C and rely on BLAS/LAPACK for Linear Algebra operations.
NumPy It is significantly faster than other Python Libraries when dealing with arrays. This is particularly true when NumPy arrays are compared with Python lists, dictionaries, and other native data structures.
NumPy is the foundation library for many other Python libraries for Scientific Computing and Data Science.
NumPy main object numpy.ndarray data type performs the most basic operations like sorting, shaping, indexing, etc.

To use NumPy, we first need to import the numpy package. It is customary to load NumPy under the np namespace. There is nothing that prevents you from using another name but np is a namespace that is easily recognized for NumPy in the Python community.

import numpy as np

Arrays vs lists and NumPy operations vs Python loops.

The two main reasons to use NumPy arrays instead of Python lists are efficiency and elegant coding. Let’s make this clear with a simple example.

Imagine that we have two lists:

N = 1000000
a = [ x for x in range(N)]
b = [ N - x for x in range(N)]

These are two Python lists and we want to compute an element-wise product of these lists. A naive programmer could think that the logical way of doing this is to write a loop to compute the product for each element and return the resulting list. Let’s write that into a function that we can time.

def naive_prod(a,b):
    c=[]
    for i in range(len(a)):
        c.append(a[i]*b[i])
    return c

naive_prod(a,b)[-3:]

[2999991, 1999996, 999999]

%timeit naive_prod(a,b)

98.1 ms ± 7.61 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

On a modern computer summing lists with 1 million elements takes a fraction of a second. Keep in mind that seconds add up when doing operations many times, so depending on the algorithm this could be a critical point for efficiency.

Imagine a new function that still takes the two lists but converts them to NumPy arrays and computes the sum

def half_way_prod(a,b):
    a=np.array(a)
    b=np.array(b)
    return a*b

half_way_prod(a,b)[-3:]

array([2999991, 1999996,  999999])

%timeit half_way_prod(a,b)

97.3 ms ± 3.55 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

There is at least 25% improvement in efficiency just by converting the lists into NumPy arrays and avoiding the loop. We can move one step forward and word from the beginning with NumPy arrays. We will see in the next section how to create arrays and operate with them. The point here is to show the importance of using NumPy arrays when working with large numerical data.

N = 1000000
a = np.arange(N)
b = np.arange(N,0,-1)

The arrays contain the same numbers but are now directly expressed as NumPy arrays. Let’s just time the product of these two arrays:

def numpy_prod(a,b):
    return a*b

%timeit numpy_prod(a,b)

1.99 ms ± 61 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)

Notice that using NumPy arrays in this simple example is two orders of magnitude faster than using Python lists and loops. The code is shorter, more elegant, and clean. We can get rid of the function itself that is now pointless for such a small operation. We can even time that:

%timeit a*b

1.86 ms ± 97.5 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

For those familiar with programming languages like C or Fortran will find that the natural code for computing the element-wise product is using a for loop:

for (i = 0; i < rows; i++) {
  c[i] = a[i]*b[i];
}

In Fortran, you can skip the loop. One advantage of a language where arrays have a privileged position.

This brings us an important lesson. Each programming language has its own natural and efficient way of coding. A literal translation from one language to another is usually a path for low performance.

Another example shows how internal operations in NumPy are more efficient than those written with explicit loops.

import time 

x=np.random.rand(1000000)
y=np.random.rand(1000000)

tic=time.time()
z=np.dot(x,y)
toc=time.time()
print('Result =',z)

print("np.dot() = "+str(1000*(toc-tic))+" ms")

z=0.0
tic=time.time()
for i in range(1000000):
    z += x[i]*y[i]
toc=time.time()
print('Result =',z)

print("Python loop = "+str(1000*(toc-tic))+" ms")

Result = 249974.76920506108
np.dot() = 0.7939338684082031 ms
Result = 249974.76920505884
Python loop = 438.3080005645752 ms

There are two sources for the extra performance of numpy.dot() over an explicit evaluation with Python loops. From one side NumPy is mapping the operation into something very similar to the equivalent C code, while the Python loop must add extra code due to the flexible types in Python.

From another side is the fact that NumPy is translating the dot product into BLAS call. An operation that depending on the BLAS implementation used could be multithreaded.

CPU and GPU have SIMD instructions (single instructions, multiple data) and NumPy is taking advantage of that. GPU can be even better. The thing to keep in mind is that we need to avoid the for loops as much as possible.

# Vector - Matrix multiplication

import time 

N=10000
x=np.random.rand(N)
y=np.random.rand(N,N)

tic=time.time()
z=np.dot(x,y)
toc=time.time()

print("np.dot() = "+str(1000*(toc-tic))+" ms")

# Exponential over a vector

tic=time.time()
z=np.exp(x)
toc=time.time()

print("np.exp() = "+str(1000*(toc-tic))+" ms")

np.dot() = 72.00837135314941 ms
np.exp() = 0.4019737243652344 ms

Now we will learn the NumPy way of working with arrays.

Array Creation

At the core of the NumPy package, is the ndarray object. A ndarray object encapsulates n-dimensional arrays of homogeneous data types, with many operations being performed in compiled code for performance.

A NumPy array is a table of elements (usually numbers), all of the same type, indexed by a tuple of non-negative integers. In NumPy, dimensions are called axes. The number of dimensions is the rank of the array; the shape of an array is a tuple of integers giving the size of the array along each dimension.

We can initialize NumPy arrays from nested Python lists, and access elements using square brackets:

a = np.array([1, 2, 3])  # Create a rank 1 array
a

array([1, 2, 3])

print(type(a), a.shape, a[0], a[1], a[2])

<class 'numpy.ndarray'> (3,) 1 2 3

a[0] = 5                 # Change an element of the array
a                

array([5, 2, 3])

b = np.array([[1,2,3],[4,5,6]])   # Create a rank 2 array
b

array([[1, 2, 3],
       [4, 5, 6]])

b.shape               

(2, 3)

print(b[0, 0], b[0, 1], b[1, 0])

1 2 4

NumPy also provides many functions to create arrays. NumPy has over 40 built-in functions for creating arrays, this is just a small sample of the functions available:

a = np.zeros((2,2))  # Create an array of all zeros
a

array([[0., 0.],
       [0., 0.]])

b = np.ones((1,2))   # Create an array of all ones
b

array([[1., 1.]])

c = np.full((2,2), 7) # Create a constant array
c

array([[7, 7],
       [7, 7]])

d = np.eye(2)        # Create a 2x2 identity matrix
d

array([[1., 0.],
       [0., 1.]])

d=np.repeat([1,2,3],4) # create a 1x12 matrix where each element is repeated 4 times
d1=np.array([1,2,3]*4) # create a 1x12 matrix where the vector is repeatec 4 times
print(d)
print(d1)

[1 1 1 1 2 2 2 2 3 3 3 3]
[1 2 3 1 2 3 1 2 3 1 2 3]

d=np.ones((3,2)) # create a matrix with ones
d

array([[1., 1.],
       [1., 1.],
       [1., 1.]])

d1=np.vstack([d,2*d]) # create a matrix stacking two, one of top of each other
d1

array([[1., 1.],
       [1., 1.],
       [1., 1.],
       [2., 2.],
       [2., 2.],
       [2., 2.]])

d1=np.hstack([d,2*d]) # create a matrix stacking two, one side of each other
d1

array([[1., 1., 2., 2.],
       [1., 1., 2., 2.],
       [1., 1., 2., 2.]])

e = np.random.random((2,2)) # Create an array filled with random values
e

array([[0.79906448, 0.51549647],
       [0.00298037, 0.00953115]])

There are a few more methods to create NumPy arrays. See the API documentation

NOTE When creating numpy arrays of dimension > 1, ensure that the shape is homogeneous. Otherwise the creation will fail

# This will fail as the lists are non-homogeneous
# np.array([[1],[1,2],[1,2,3]], dtype=np.float32)

To create arrays evenly distributed we can do it two ways, one where we specify the beginning, the end and the stepsize or by defining the min, the max and the number of numbers we want in that interval

a=np.arange(0,10,2)
a

array([0, 2, 4, 6, 8])

b=np.linspace(0,10,8)
b

array([ 0.        ,  1.42857143,  2.85714286,  4.28571429,  5.71428571,
        7.14285714,  8.57142857, 10.        ])

Array indexing, slicing and striding

NumPy arrays can be indexed using the standard Python x[obj] syntax, where x is the array and obj the selection.

In Python, x[(exp1, exp2, ..., expN)] is equivalent to x[exp1, exp2, ..., expN]. This allows a natural way of expressing multidimensional arrays.

Slicing: Similar to Python lists, NumPy arrays can be sliced. Since arrays may be multidimensional, you must specify a slice for each dimension of the array.

Basic slicing occurs when obj is a slice object (constructed by start:stop:step notation inside of brackets), an integer, or a tuple of slice objects and integers. Ellipsis (...) and newaxis objects can be interspersed with these as well.

# Create the following rank 2 arrays with shape (3, 4)
# [[ 1  2  3  4]
#  [ 5  6  7  8]
#  [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
a

array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
#  [6 7]]
b = a[:2, 1:3]
b

array([[2, 3],
       [6, 7]])

b = a[1:3, 0:3:2]  # going over y-axis from 0 to 3 in steps of 2
b

array([[ 5,  7],
       [ 9, 11]])

print(a[-1,::2])  # going over the last row and printing every two elements

[ 9 11]

A slice of an array is a view into the same data, so modifying it will modify the original array.

print(a[1, 0])
b[0, 0] = 77    # b[0, 0] is the same piece of data as a[1, 0]
print(a[1, 0])

5
77

array([[ 1,  2,  3,  4],
       [77,  6,  7,  8],
       [ 9, 10, 11, 12]])

You can also mix integer indexing with slice indexing. However, doing so will yield an array of lower ranks than the original array. Note that this is quite different from the way that MATLAB handles array slicing:

# Create the following rank 2 arrays with shape (3, 4)
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
a

array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

Two ways of accessing the data in the middle row of the array. Mixing integer indexing with slices yields an array of lower rank, while using only slices yields an array of the same rank as the original array:

row_r1 = a[1, :]    # Rank 1 view of the second row of a  
row_r2 = a[1:2, :]  # Rank 2 view of the second row of a
row_r3 = a[[1], :]  # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) 
print(row_r2, row_r2.shape)
print(row_r3, row_r3.shape)

[5 6 7 8] (4,)
[[5 6 7 8]] (1, 4)
[[5 6 7 8]] (1, 4)

# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape)
print()
print(col_r2, col_r2.shape)

[ 2  6 10] (3,)

[[ 2]
 [ 6]
 [10]] (3, 1)

Integer array indexing: When you index into NumPy arrays using slicing, the resulting array view will always be a subarray of the original array. In contrast, integer array indexing allows you to construct arbitrary arrays using the data from another array. Here is an example:

a = np.array([[1,2], [3, 4], [5, 6]])

# An example of integer array indexing.
# The returned array will have shape (3,) and 
print(a[[0, 1, 2], [0, 1, 0]])

# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]]))

[1 4 5]
[1 4 5]

# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]])

# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]]))

[2 2]
[2 2]

One useful trick with integer array indexing is selecting or mutating one element from each row of a matrix:

# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
a

array([[ 1,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12]])

# Create an array of indices
b = np.array([0, 2, 0, 1])

# Select one element from each row of a using the indices in b
print(a[np.arange(4), b])  # Prints "[ 1  6  7 11]"

[ 1  6  7 11]

# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a)

[[11  2  3]
 [ 4  5 16]
 [17  8  9]
 [10 21 12]]

Boolean array indexing: Boolean array indexing lets you pick out arbitrary elements of an array. Frequently this type of indexing is used to select the elements of an array that satisfy some condition. Here is an example:

a = np.array([[1,2], [3, 4], [5, 6]])

bool_idx = (a > 2)  # Find the elements of a that are bigger than 2;
                    # this returns a NumPy array of Booleans of the same
                    # shape as a, where each slot of bool_idx tells
                    # whether that element of a is > 2.

bool_idx

array([[False, False],
       [ True,  True],
       [ True,  True]])

# We use boolean array indexing to construct a rank 1 array
# consisting of the elements of a corresponding to the True values
# of bool_idx
print(a[bool_idx])

# We can do all of the above in a single concise statement:
print(a[a > 2])

[3 4 5 6]
[3 4 5 6]

Slice objects can be used in the construction in place of the [start:stop:step] notation.

a=np.arange(100).reshape((10,10))
a

array([[ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
       [20, 21, 22, 23, 24, 25, 26, 27, 28, 29],
       [30, 31, 32, 33, 34, 35, 36, 37, 38, 39],
       [40, 41, 42, 43, 44, 45, 46, 47, 48, 49],
       [50, 51, 52, 53, 54, 55, 56, 57, 58, 59],
       [60, 61, 62, 63, 64, 65, 66, 67, 68, 69],
       [70, 71, 72, 73, 74, 75, 76, 77, 78, 79],
       [80, 81, 82, 83, 84, 85, 86, 87, 88, 89],
       [90, 91, 92, 93, 94, 95, 96, 97, 98, 99]])

obj = (slice(1, 10, 5), slice(None, None, -1))
a[obj]

array([[19, 18, 17, 16, 15, 14, 13, 12, 11, 10],
       [69, 68, 67, 66, 65, 64, 63, 62, 61, 60]])

NOTE NumPy uses C-order indexing. That means that the last index usually represents the most rapidly changing memory location, unlike Fortran, where the first index represents the most rapidly changing location in memory. This difference is important for performance considerations.

Elipsis (...) is used to expand the number of : objects as needed for the selection tuple to index all dimensions. Only one ellipsis can be present on a slice. Example:

x = np.arange(6).reshape(2,3,1)
x

array([[[0],
        [1],
        [2]],

       [[3],
        [4],
        [5]]])

x[...,0]

array([[0, 1, 2],
       [3, 4, 5]])

x[...,0].shape

(2, 3)

New dimensions can be added via the newaxis object in the selection tuple. newaxis is an alias for None. They both can be used to increase the dimensionality of an array. These operations return views of the array. Different from a reshaping that will change the dimensionality of the array.

x[:, np.newaxis, :, :].shape

(2, 1, 3, 1)

x[:, None, :, :].shape

(2, 1, 3, 1)

x.shape

(2, 3, 1)

For brevity, we have left out a lot of details about NumPy array indexing; if you want to know more you should read the NumPy User Guide on indexing

Advanced indexing

Advanced indexing happens when the obj is a non-tuple sequence object, a ndarray (of data type integer or bool), or a tuple with at least one sequence object or ndarray (of data type integer or bool).

Advanced indexing return copies, different from slices that return views, ie reference the same array.

There are two types of advanced indexing: integer and Boolean.

Integer array indexing allows selection of arbitrary items in the array based on their N-dimensional index. Each integer array represents several indices into that dimension.

x = np.arange(11,21)
x

array([11, 12, 13, 14, 15, 16, 17, 18, 19, 20])

x[np.array([3, 3, 1, 8])]

array([14, 14, 12, 19])

x[np.array([3, 3, -3, 8])]

array([14, 14, 18, 19])

Boolean indexing happens when the obj is an array of booleans

x = np.arange(35).reshape(5, 7)
x

array([[ 0,  1,  2,  3,  4,  5,  6],
       [ 7,  8,  9, 10, 11, 12, 13],
       [14, 15, 16, 17, 18, 19, 20],
       [21, 22, 23, 24, 25, 26, 27],
       [28, 29, 30, 31, 32, 33, 34]])

b = x > 20
b

array([[False, False, False, False, False, False, False],
       [False, False, False, False, False, False, False],
       [False, False, False, False, False, False, False],
       [ True,  True,  True,  True,  True,  True,  True],
       [ True,  True,  True,  True,  True,  True,  True]])

b[:, 5]
x[b[:, 5]]

array([[21, 22, 23, 24, 25, 26, 27],
       [28, 29, 30, 31, 32, 33, 34]])

This is different from the slice x[b] which is NumPy array flattened.

x[b[:,:]]

array([21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34])

x[b]

array([21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34])

Creating Arrays from a file

NumPy provides several functions to create arrays from tabular data.

The function loadtxt can be used for reading from files with no missing values.

The function genfromtxt is slower but is capable of handling missing values.

In general for large arrays, it is better to avoid reading and writing data as text files. There are specialized formats such as HDF5, NetCDF, and others that will store data in a binary format.

To read a CSV file with loadtxt you can use:

x = np.loadtxt('./data/heart.csv', delimiter=',', skiprows=1)
x

array([[63.,  1.,  3., ...,  0.,  1.,  1.],
       [37.,  1.,  2., ...,  0.,  2.,  1.],
       [41.,  0.,  1., ...,  0.,  2.,  1.],
       ...,
       [68.,  1.,  0., ...,  2.,  3.,  0.],
       [57.,  1.,  0., ...,  1.,  3.,  0.],
       [57.,  0.,  1., ...,  1.,  2.,  0.]])

x.shape

(303, 14)

Without skipping the first line genfromtxt will replace the values with nan. The function loadtxt will return an error.

np.genfromtxt('./data/heart.csv', delimiter=",")

array([[nan, nan, nan, ..., nan, nan, nan],
       [63.,  1.,  3., ...,  0.,  1.,  1.],
       [37.,  1.,  2., ...,  0.,  2.,  1.],
       ...,
       [68.,  1.,  0., ...,  2.,  3.,  0.],
       [57.,  1.,  0., ...,  1.,  3.,  0.],
       [57.,  0.,  1., ...,  1.,  2.,  0.]])

Array Data Types

Every NumPy array is a grid of elements of the same type. NumPy provides a large set of numeric data types that you can use to construct arrays. NumPy tries to guess a datatype when you create an array, but functions that construct arrays usually also include an optional argument to explicitly specify the datatype. Here is an example:

x = np.array([1, 2])  # Let numpy choose the datatype
y = np.array([1.0, 2.0])  # Let numpy choose the datatype
z = np.array([1, 2], dtype=np.int64)  # Force a particular datatype

print(x.dtype, y.dtype, z.dtype)

int64 float64 int64

You can read all about NumPy datatypes in the NumPy User Guide.

Universal functions (ufunc)

A ufunc is a “vectorized” wrapper for a function that takes a fixed number of specific inputs and produces a fixed number of specific outputs.

There are many universal functions implemented to operate elementwise on NumPy arrays, and are available both as operator overloads and as functions in the NumPy module:

x = np.array([[1,2],[3,4]], dtype=np.float64)
y = np.array([[5,6],[7,8]], dtype=np.float64)

# Elementwise sum; both produce the array
print(x + y)
print(np.add(x, y))

[[ 6.  8.]
 [10. 12.]]
[[ 6.  8.]
 [10. 12.]]

# Elementwise difference; both produce the array
print(x - y)
print(np.subtract(x, y))

[[-4. -4.]
 [-4. -4.]]
[[-4. -4.]
 [-4. -4.]]

# Elementwise product; both produce the array
print(x * y)
print(np.multiply(x, y))

[[ 5. 12.]
 [21. 32.]]
[[ 5. 12.]
 [21. 32.]]

# Elementwise division; both produce the array
# [[ 0.2         0.33333333]
#  [ 0.42857143  0.5       ]]
print(x / y)
print(np.divide(x, y))

[[0.2        0.33333333]
 [0.42857143 0.5       ]]
[[0.2        0.33333333]
 [0.42857143 0.5       ]]

# Elementwise square root; produces the array
# [[ 1.          1.41421356]
#  [ 1.73205081  2.        ]]
print(np.sqrt(x))

[[1.         1.41421356]
 [1.73205081 2.        ]]

Note that, unlike MATLAB, * is elementwise multiplication, not matrix multiplication. We instead use the dot function to compute the inner products of vectors, multiply a vector by a matrix, and multiply matrices. dot is available both as a function in the NumPy module and as an instance method of array objects:

x = np.array([[1,2],[3,4]])
y = np.array([[5,6],[7,8]])

v = np.array([9,10])
w = np.array([11, 12])

# Inner product of vectors; both produce 219
print(v.dot(w))
print(np.dot(v, w))

219
219

# Matrix / vector product; both produce the rank 1 array [29 67]
print(x.dot(v))
print(np.dot(x, v))
print(np.dot(x.T, v)) # now with the transpose of x

[29 67]
[29 67]
[39 58]

# Matrix / matrix product; both produce the rank 2 array
# [[19 22]
#  [43 50]]
print(x.dot(y))
print(np.dot(x, y))

[[19 22]
 [43 50]]
[[19 22]
 [43 50]]

print(x.dtype)
x=x.astype('f')
print(x.dtype)

int64
float32

NumPy provides many useful functions for performing computations on arrays; one of the most useful is sum:

x = np.array([[1,2],[3,4]])

print(np.sum(x))  # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0))  # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1))  # Compute sum of each row; prints "[3 7]"

10
[4 6]
[3 7]

print(x.mean())
print(x.std())
print(x.sum())
print(x.min(),x.argmin())
print(x.max(),x.argmax())
print(x**2)

2.5
1.118033988749895
10
1 0
4 3
[[ 1  4]
 [ 9 16]]

You can find the full list of mathematical functions provided by NumPy in the documentation.

Apart from computing mathematical functions using arrays, we frequently need to reshape or otherwise manipulate data in arrays. The simplest example of this type of operation is transposing a matrix; to transpose a matrix, simply use the T attribute of an array object:

print(x)
print(x.T)

[[1 2]
 [3 4]]
[[1 3]
 [2 4]]

v = np.array([[1,2,3]])
print(v) 
print(v.T)

[[1 2 3]]
[[1]
 [2]
 [3]]

Copies and views

NumPy arrays could contain many values. It could be inefficient to create copies and many operations in NumPy are references to the original data.

When operating on NumPy arrays, it is possible to access the internal data buffer directly using a view without copying data around. This ensures good performance but can also cause unwanted problems if the user is not aware of how this works. Hence, it is important to know the difference between these two terms and to know which operations return copies and which return views.

Consider a 2D array:

a=np.arange(20)
a.resize((4,5))
a

array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14],
       [15, 16, 17, 18, 19]])

a[a>10]=10   # caping the maximum value of the array to 10
a

array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 10, 10, 10, 10],
       [10, 10, 10, 10, 10]])

# we create a slice of an into r (This is a new view)
r=a[1:3,2:4]
r

array([[ 7,  8],
       [10, 10]])

#we assign 99.0 to all elements of r
r[:]=99
# see that elements in a have changed!!!
print(a)
print(r)

[[ 0  1  2  3  4]
 [ 5  6 99 99  9]
 [10 10 99 99 10]
 [10 10 10 10 10]]
[[99 99]
 [99 99]]

A copy is a method that will return a shallow copy of the elements in the array.

# instead if we want just a copy of the original array
a=np.arange(20)
a.resize((4,5))
r=a[:2,:2].copy()
r[:]=99.0
print(a)
print(r)

[[ 0  1  2  3  4]
 [ 5  6  7  8  9]
 [10 11 12 13 14]
 [15 16 17 18 19]]
[[99 99]
 [99 99]]

Broadcasting

The term broadcasting describes how NumPy treats arrays with different shapes during arithmetic operations.

Under some constraints, smaller arrays can be “broadcasted” to operate over a larger array to appear as they have compatible shapes.

Broadcasting provides a means of vectorizing array operations so that looping occurs in C instead of Python. No extra copies of arrays are taking place which usually leads to efficient algorithm implementations.

a=np.array([[12.0,0.0,8.0,5.0],[4.8,3.2,1.4,2.5],[1.2,8.0,1.2,3.2]])
a

array([[12. ,  0. ,  8. ,  5. ],
       [ 4.8,  3.2,  1.4,  2.5],
       [ 1.2,  8. ,  1.2,  3.2]])

sum_columns=np.sum(a,axis=0)
print(sum_columns)
print(sum_columns.shape)

[18.  11.2 10.6 10.7]
(4,)

# Divide each column per the sum over the whole column
# here the broadcasting is to divide the matrix a, each column by a different number that comes from a vector
percentage=100*a/sum_columns.reshape(1,4)

print(percentage)

percentage=100*a/sum_columns

print(percentage)

[[66.66666667  0.         75.47169811 46.72897196]
 [26.66666667 28.57142857 13.20754717 23.36448598]
 [ 6.66666667 71.42857143 11.32075472 29.90654206]]
[[66.66666667  0.         75.47169811 46.72897196]
 [26.66666667 28.57142857 13.20754717 23.36448598]
 [ 6.66666667 71.42857143 11.32075472 29.90654206]]

Broadcasting is a powerful mechanism that allows NumPy to work with arrays of different shapes when performing arithmetic operations. Frequently we have a smaller array and a larger array, and we want to use the smaller array multiple times to perform some operation on the larger array.

For example, suppose that we want to add a constant vector to each row of a matrix. We could do it like this:

# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.arange(1,13).reshape(4,3)
x

array([[ 1,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12]])

print(x.shape)

(4, 3)

v = np.array([1, 0, 1])
print(v.shape)
y = np.empty_like(x)   # Create an empty matrix with the same shape as x

(3,)

# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
    y[i, :] = x[i, :] + v

print(y)

[[ 2  2  4]
 [ 5  5  7]
 [ 8  8 10]
 [11 11 13]]

This works; however when the matrix x is very large, computing an explicit loop in Python could be slow. Note that adding the vector v to each row of the matrix x is equivalent to forming a matrix vv by stacking multiple copies of v vertically, then performing an elementwise summation of x and vv. We could implement this approach like this:

vv = np.tile(v, (4, 1))  # Stack 4 copies of v on top of each other
print(vv)                # Prints "[[1 0 1]
                         #          [1 0 1]                  
                         #          [1 0 1]
                         #          [1 0 1]]"

[[1 0 1]
 [1 0 1]
 [1 0 1]
 [1 0 1]]

y = x + vv  # Add x and vv elementwise
print(y)

[[ 2  2  4]
 [ 5  5  7]
 [ 8  8 10]
 [11 11 13]]

NumPy broadcasting allows us to perform this computation without actually creating multiple copies of v. Consider this version, using broadcasting:

# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.arange(1,13).reshape(4,3)
v = np.array([1, 0, 1])

y = x + v  # Add v to each row of x using broadcasting
print(y)

[[ 2  2  4]
 [ 5  5  7]
 [ 8  8 10]
 [11 11 13]]

The line y = x + v works even though x has shape (4, 3) and v has shape (3,) due to broadcasting; this line works as if v had shape (4, 3), where each row was a copy of v, and the sum was performed elementwise.

Broadcasting two arrays together follows these rules:

If the arrays do not have the same rank, prepend the shape of the lower rank array with 1s until both shapes have the same length.
The two arrays are said to be compatible in a dimension if they have the same size in the dimension, or if one of the arrays has size 1 in that dimension.
The arrays can be broadcast together if they are compatible in all dimensions.
After broadcasting, each array behaves as if it had a shape equal to the elementwise maximum of shapes of the two input arrays.
In any dimension where one array had a size 1 and the other array had a size greater than 1, the first array behaves as if it were copied along that dimension

If this explanation does not make sense, try reading the explanation from the documentation or several tutorias as tutorial_1, tutorial_2.

Functions that support broadcasting are known as universal functions. You can find the list of all universal functions in the documentation.

Here are some applications of broadcasting:

# Compute outer product of vectors
v = np.array([1,2,3])  # v has shape (3,)
w = np.array([4,5])    # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:

np.reshape(v, (3, 1)) * w

array([[ 4,  5],
       [ 8, 10],
       [12, 15]])

# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:

x + v

array([[2, 4, 6],
       [5, 7, 9]])

# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix

(x.T + w).T

array([[ 5,  6,  7],
       [ 9, 10, 11]])

# Another solution is to reshape w to be a row vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.

x + np.reshape(w, (2, 1))

array([[ 5,  6,  7],
       [ 9, 10, 11]])

# Multiply a matrix by a constant:
# x has shape (2, 3). NumPy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:

x * 2

array([[ 2,  4,  6],
       [ 8, 10, 12]])

Broadcasting typically makes your code more concise and faster, so you should strive to use it where possible.

Functional programming

Functional programming is a programming paradigm in which the primary method of computation is evaluation of functions.

Python is multiparadigm, meaning that it offers the possibility of being procedural, object-oriented or using functional programming or a mix of all these. There is a HOWTO devoted to Functional Programming in the Official Python Documentation

There are several methods in NumPy that take Python functions as arguments and these functions are often used to process NumPy arrays and avoid the explicit call for loops.

`apply_along_axis`

The function apply_along_axis is used to apply a function to 1-D slices along the given axis. Example:

def max_min(a):
    """Differnce between the maximum value and the minimum of a 1-D array"""
    return max(a)-min(a)

b = np.arange(1,17).reshape(4,4)
b

array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12],
       [13, 14, 15, 16]])

np.apply_along_axis(max_min, 0, b)

array([12, 12, 12, 12])

np.apply_along_axis(max_min, 1, b)

array([3, 3, 3, 3])

The axis is defined by the dimension that you are leaving free, ie the dimension with the colon (:). Other dimensions are fixed to return 1-D slices. See for example:

b[:,1] # axis=0

array([ 2,  6, 10, 14])

b[1,:] # axis=1

array([5, 6, 7, 8])

`apply_over_axes`

The function apply_over_axes can be considered as the complement of apply_along_axis. Instead of applying a function to 1-D slices. It applies the function to N-1 slices.

apply_over_axes(func, a, axes) apply a function func repeatedly over multiple axes of array a.

func is called as res = func(a, axis), where the axis is the first element of axes. The result res of the function call must have either the same dimensions as a or one less dimension. If res has one less dimension than a, a dimension is inserted before the axis. The call to func is then repeated for each axis in axes, with res as the first argument.

Consider this example with a 3D array:

a = np.arange(27).reshape(3,3,3)
a

array([[[ 0,  1,  2],
        [ 3,  4,  5],
        [ 6,  7,  8]],

       [[ 9, 10, 11],
        [12, 13, 14],
        [15, 16, 17]],

       [[18, 19, 20],
        [21, 22, 23],
        [24, 25, 26]]])

b= np.apply_over_axes(np.sum, a, [0,2])
b

array([[[ 90],
        [117],
        [144]]])

b.shape

(1, 3, 1)

a[:,0,:]

array([[ 0,  1,  2],
       [ 9, 10, 11],
       [18, 19, 20]])

np.sum(a[:,0])

a[:,1,:]

array([[ 3,  4,  5],
       [12, 13, 14],
       [21, 22, 23]])

np.sum(a[:,1])

a[:,2,:]

array([[ 6,  7,  8],
       [15, 16, 17],
       [24, 25, 26]])

np.sum(a[:,2,:])

vectorize

The method vectorize returns a vectorized function which takes a nested sequence of objects or NumPy arrays as inputs and returns a single NumPy array or a tuple of NumPy arrays. The vectorized function evaluates pyfunc over successive tuples of the input arrays like the python map function, except it uses the broadcasting rules of NumPy.

We will see how broadcasting works in the next section.

Let’s see with a simple example:

def myfunc(a, b):
    "Return a-b if a>b, otherwise return a+b"
    if a > b:
        return a - b
    else:
        return a + b

a = np.arange(15,25,)
b = np.arange(10,30,2)

a.shape

(10,)

b.shape

(10,)

array([15, 16, 17, 18, 19, 20, 21, 22, 23, 24])

array([10, 12, 14, 16, 18, 20, 22, 24, 26, 28])

This function will fail if used directly over NumPy arrays as the comparison operations will return arrays which will not be accepted by the if conditional.

#myfunc(a,b)

The solution is to vectorize the function

vfunc = np.vectorize(myfunc)

Now the function can operate element-wise over the two input arrays

vfunc(a,b)

array([ 5,  4,  3,  2,  1, 40, 43, 46, 49, 52])

The extra advantage is that broadcastable arguments can work too. For example, if the second argument is just a scalar, it will be promoted to a constant array all without incurring on actual storage of the array.

vfunc(b, 20)

array([30, 32, 34, 36, 38, 40,  2,  4,  6,  8])

The function above will produce the same result as the function below, without the extra memory usage:

vfunc(b, np.full_like(b,20))

array([30, 32, 34, 36, 38, 40,  2,  4,  6,  8])

`frompyfunc`

Takes an arbitrary Python function and returns a NumPy ufunc.

Can be used, for example, to add broadcasting to a built-in Python function

from math import cos, sin

def cos2sin2(theta1, theta2):
    return cos(theta1)**2 + sin(theta2)**2

a=np.arange(np.pi, 2*np.pi, 0.1)
b=np.arange(np.pi, 2*np.pi, 0.1)

This function will fail if applied to two arrays

#cos2sin2(a,b)

cos2sin2_array = np.frompyfunc(cos2sin2, 2, 1)

cos2sin2_array(a,b).astype(np.float32)

array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
       1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
      dtype=float32)

Using broadcasting:

cos2sin2_array(a, np.pi).astype(np.float32)

array([1.0000000e+00, 9.9003327e-01, 9.6053052e-01, 9.1266781e-01,
       8.4835333e-01, 7.7015114e-01, 6.8117887e-01, 5.8498359e-01,
       4.8540023e-01, 3.8639894e-01, 2.9192659e-01, 2.0574944e-01,
       1.3130315e-01, 7.1555622e-02, 2.8888829e-02, 5.0037517e-03,
       8.5261208e-04, 1.6600903e-02, 5.1620793e-02, 1.0451614e-01,
       1.7317820e-01, 2.5486958e-01, 3.4633356e-01, 4.4392374e-01,
       5.4374951e-01, 6.4183110e-01, 7.3425835e-01, 8.1734645e-01,
       8.8778293e-01, 9.4275975e-01, 9.8008513e-01, 9.9827105e-01],
      dtype=float32)

def cos2_sin2(theta1, theta2):
    return cos(theta1)**2 + sin(theta2)**2, cos(theta1)**2 - sin(theta2)**2

cos2_sin2_array = np.frompyfunc(cos2_sin2, 2, 2)

cos2_sin2_array(a,b)

(array([1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
        1.0, 1.0, 1.0, 1.0, 1.0, 0.9999999999999999, 0.9999999999999999,
        1.0, 1.0, 1.0, 1.0000000000000002, 1.0, 0.9999999999999998, 1.0,
        1.0, 1.0, 1.0, 1.0, 1.0], dtype=object),
 array([1.0, 0.9800665778412417, 0.9210609940028851, 0.8253356149096782,
        0.696706709347165, 0.5403023058681391, 0.3623577544766729,
        0.16996714290023984, -0.02919952230128975, -0.2272020946930875,
        -0.4161468365471438, -0.5885011172553479, -0.7373937155412469,
        -0.8568887533689479, -0.942222340668659, -0.9899924966004459,
        -0.9982947757947529, -0.9667981925794604, -0.8967584163341457,
        -0.7909677119144142, -0.6536436208636095, -0.4902608213406974,
        -0.3073328699784162, -0.1121525269350499, 0.08749898343945067,
        0.28366218546322947, 0.46851667130038077, 0.6346928759426387,
        0.7755658785102528, 0.8855195169413208, 0.9601702866503675,
        0.9965420970232179], dtype=object))

`piecewise`

Given a set of conditions and corresponding functions, evaluate each function on the input data wherever its condition is true.

x = np.linspace(-2.5, 2.5, 11)
np.piecewise(x, [x < 0, x >= 0], [0, lambda x: x])

array([0. , 0. , 0. , 0. , 0. , 0. , 0.5, 1. , 1.5, 2. , 2.5])

More about NumPy

Before we end, let us see some details about vectors that are not trivial in python

a=np.random.rand(8)
print(a)
print(a.shape)

[0.74307734 0.02455649 0.55808347 0.50537739 0.08364459 0.09162871
 0.90721139 0.9711414 ]
(8,)

The dimension of this vector is not (8,1) or (1,8), it is (8,) which is called a rank 1 array and it is neither a column nor a raw vector. Let’s see the effects

print(np.dot(a,a.T))
print(np.dot(a,a))

2.9011707791645622
2.9011707791645622

Compare this to

a=np.random.rand(8,1)
print(a)

[[0.36246396]
 [0.23574612]
 [0.94928379]
 [0.80199144]
 [0.74450619]
 [0.07013615]
 [0.90001147]
 [0.62017984]]

print(np.dot(a,a.T))
print(a.shape)
#print(np.dot(a,a))
print(np.dot(a.T,a))

[[0.13138012 0.08544947 0.34408116 0.29069299 0.26985666 0.02542183
  0.32622172 0.22479284]
 [0.08544947 0.05557623 0.22378996 0.18906637 0.17551444 0.01653433
  0.21217421 0.14620499]
 [0.34408116 0.22378996 0.90113971 0.76131747 0.70674765 0.06657911
  0.85436629 0.58872666]
 [0.29069299 0.18906637 0.76131747 0.64319028 0.59708759 0.05624859
  0.7218015  0.49737892]
 [0.26985666 0.17551444 0.70674765 0.59708759 0.55428946 0.0522168
  0.67006411 0.46172773]
 [0.02542183 0.01653433 0.06657911 0.05624859 0.0522168  0.00491908
  0.06312334 0.04349703]
 [0.32622172 0.21217421 0.85436629 0.7218015  0.67006411 0.06312334
  0.81002065 0.55816897]
 [0.22479284 0.14620499 0.58872666 0.49737892 0.46172773 0.04349703
  0.55816897 0.38462303]]
(8, 1)
[[3.48513855]]

Therefore, unless you know what you are doing, please keep the definitions of the matrix as (8,1) for example. You can check dimensionality by using assert(a.shape==(8,1)) and you can reshape your vectors as a.reshape((1,8))

This brief overview has touched on many of the important things that you need to know about NumPy, but is far from complete. Check out the numpy reference to find out much more about NumPy.

Acknowledgments and References

This Notebook has been adapted by Guillermo Avendaño (WVU), Jose Rogan (Universidad de Chile) and Aldo Humberto Romero (WVU) from the Tutorials for Stanford cs228 and cs231n. A large part of the info was also built from scratch. In turn, that material was adapted by Volodymyr Kuleshov and Isaac Caswell from the CS231n Python tutorial by Justin Johnson (http://cs231n.github.io/python-numpy-tutorial/). Another good resource, in particular, if you want to just look for the answer to a specific question is planetpython.org, in particular for data science.

Changes to the original tutorial include strict Python 3 formats and a split of the material to fit a series of lessons on Python Programming for WVU’s faculty and graduate students.

The support of the National Science Foundation and the US Department of Energy under projects: DMREF-NSF 1434897, NSF OAC-1740111 and DOE DE-SC0016176 is recognized.

Back of the Book

plt.figure(figsize=(3,3))
n = chapter_number
maxt=(2*(n-1)+3)*np.pi/2
t = np.linspace(np.pi/2, maxt, 1000)
tt= 1.0/(t+0.01)
x = (maxt-t)*np.cos(t)**3
y = t*np.sqrt(np.abs(np.cos(t))) + np.sin(0.3*t)*np.cos(2*t)
plt.plot(x, y, c="green")
plt.axis('off');

png

end = time.time()
print(f'Chapter {chapter_number} run in {int(end - start):d} seconds')

Chapter 4 run in 47 seconds

Key Points

numpy is the standard de-facto for numerical calculations at large scale in Python

Python Scripting for HPC

Overview

Teaching: 90 min
Exercises: 30 min

Topics

How to use numpy to manipulate multidimensional arrays in Python?

How I split and select portions of a numpy array?

Objectives

Learn to create, manipulate, and slice numpy arrays

Python Programming for Scientists in a hurry

Chapter 7. Pandas

Guillermo Avendaño Franco
Aldo Humberto Romero

List of Notebooks

Language Syntax
Standard Library
Scientific Packages
NumPy
Matplotlib
SciPy
Pandas [This notebook]
Cython
Parallel Computing

Setup

%load_ext watermark

%watermark

Last updated: 2024-07-26T13:27:25.045249-04:00

Python implementation: CPython
Python version       : 3.11.7
IPython version      : 8.14.0

Compiler    : Clang 12.0.0 (clang-1200.0.32.29)
OS          : Darwin
Release     : 20.6.0
Machine     : x86_64
Processor   : i386
CPU cores   : 8
Architecture: 64bit

import os
import time
start = time.time()
chapter_number = 7
import matplotlib
%matplotlib inline
%load_ext autoreload
%autoreload 2

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

%watermark -iv

matplotlib: 3.8.2
pandas    : 1.5.3
numpy     : 1.26.2

Pandas (Data Analysis)

In this tutorial, we will cover:

Create DataFrames directly and from several file formats
Extract specific rows and columns

The purpose of this notebook is to show the basic elements that make Pandas a very effective tool for data analysis. In particular the focus will be on dealing with scientific data rather than a more broad “another dataset” approach from most tutorials of this kind.

pandas is an open source, BSD-licensed library providing high-performance, easy-to-use data structures and data analysis tools for the Python programming language. It was created by Wes McKinney.

pandas is a NumFOCUS-sponsored project. It is a well-established API and it is the foundation of several other packages used in data analysis, data mining, and machine learning applications.

Pandas is one of the most often asked questions on Stack Overflow, in part due to its rising popularity but also due to the versatility in manipulating data.

Pandas can be used also in scripts and bigger applications. However, it is easier to learn it from an interactive computing perspective. So we will use this notebook for that purpose. For anything that is not covered here, there are two good resources you need to consider. One is the pandas’ webpage and the other one is stackoverflow.com.

The command above exposes all the functionality of pandas under the pd namespace. This namespace is optional and its name arbitrary but with time it has been converted into the-facto usage.

Pandas deals with basically two kinds of data: Series and Dataframe. Series is just a collection of values like

fibo=pd.Series([1,1,2,3,5,8,13])

fibo

   1
   1
   2
   3
   5
   8
  13
dtype: int64

#Let us see other example
a={'France':'Paris','Colombia':'Bogota','Argentina':'Buenos Aires','Chile':'Santiago'}
b=pd.Series(a)
print(b)

France              Paris
Colombia           Bogota
Argentina    Buenos Aires
Chile            Santiago
dtype: object

print(b.index)

Index(['France', 'Colombia', 'Argentina', 'Chile'], dtype='object')

#We can also create the list by passing the index as a list
c=pd.Series(['France','Colombia','Argentina','Chile'],index=['Paris','Bogota','Buenos Aires','Santiago'])
print(c)

Paris              France
Bogota           Colombia
Buenos Aires    Argentina
Santiago            Chile
dtype: object

# to look for the 3rd Capital in this list. Remember that here the country name is the indexing
print(b.iloc[2])
# to look for the capital of Argentina
print(b.loc['Argentina'])
# we can use the following but we have to be careful
print(b[2])
#why? because
a={1:'France',2:'Colombia',3:'Argentina',4:'Chile'}
p=pd.Series(a)
#here we will print what happens with index 2, no by the "position 2". For that reason
# it is always better to use iloc when querying a position
print(p[2])

Buenos Aires
Buenos Aires
Buenos Aires
Colombia

data1=['a','b','c','d',None]
pd.Series(data1)

     a
     b
     c
     d
  None
dtype: object

#Here we stress that NaN is the same as None but it is number
data2=[1,2,2,3,None]
pd.Series(data2)

  1.0
  2.0
  2.0
  3.0
  NaN
dtype: float64

#To see why this is important, let's see what Numpy says about None
import numpy as np
print(np.nan == None)
# more interesting is if we compare np.nan with itself
print(np.nan == np.nan)
#THerefore we need a special function to check the existence of a Nan such as
print(np.isnan(np.nan))

False
False
True

# we can also mix types
a=pd.Series([1,2,3])
print(a)
#now we add a new entry
a.loc['New capital']='None'
print(a)

0    1
1    2
2    3
dtype: int64
0                 1
1                 2
2                 3
New capital    None
dtype: object

Dataframes are tables, consider for example this table with the Boiling Points for common Liquids and Gases at Atmospheric pressure. Data from https://www.engineeringtoolbox.com/boiling-points-fluids-gases-d_155.html

Product	Boiling Point (C)	Boiling Point (F)
Acetylene	-84	-119
Ammonia	-35.5	-28.1
Ethanol	78.4	173
Isopropyl Alcohol	80.3	177
Mercury	356.9	675.1
Methane	-161.5	-258.69
Methanol	66	151
Propane	-42.04	-43.67
Sulfuric Acid	330	626
Water	100	212

This table can be converted into a Pandas Dataframe using a python dictionary as an entry.

temps={'F': [-84, -35.5, 78.4, 80.3, 356.9, -161.5, 66, -42.04, 330, 100], 
       'C':[-119,-28.1, 173, 177, 675.1, -258.69, 151, -43.67, 626, 212]}

pd.DataFrame(temps)

	F	C
0	-84.00	-119.00
1	-35.50	-28.10
2	78.40	173.00
3	80.30	177.00
4	356.90	675.10
5	-161.50	-258.69
6	66.00	151.00
7	-42.04	-43.67
8	330.00	626.00
9	100.00	212.00

How did that work?

Each (key, value) item in temps corresponds to a column in the resulting DataFrame.

The Index of this DataFrame was given to us on creation as the numbers 0-9. To complete the table, let’s add the names of the substances for which the boiling point was measured.

indices=['Acetylene', 'Ammonia', 'Ethanol', 'Isopropyl Alchol', 
         'Mercury', 'Methane', 'Methanol', 'Propane', 'Sulfuric Acid', 'Water']

boiling = pd.DataFrame(temps, index=indices)
boiling

	F	C
Acetylene	-84.00	-119.00
Ammonia	-35.50	-28.10
Ethanol	78.40	173.00
Isopropyl Alchol	80.30	177.00
Mercury	356.90	675.10
Methane	-161.50	-258.69
Methanol	66.00	151.00
Propane	-42.04	-43.67
Sulfuric Acid	330.00	626.00
Water	100.00	212.00

A pandas data frame arranges data into columns and rows, each column has a tag and each row is identified with an index. If the index is not declared, a number will be used instead.

Before we now play with the data, I would like to stress that one of the differences with NumPy is how we want to manage missing data. Let’s see two examples

Extracting columns and rows

Columns can be extracted using the name of the column, there are two ways of extracting them, as series or as another data frame. As Series will be:

boiling['F']

Acetylene           -84.00
Ammonia             -35.50
Ethanol              78.40
Isopropyl Alchol     80.30
Mercury             356.90
Methane            -161.50
Methanol             66.00
Propane             -42.04
Sulfuric Acid       330.00
Water               100.00
Name: F, dtype: float64

type(_)

pandas.core.series.Series

As data frame, a double bracket is used

boiling[['F']]

	F
Acetylene	-84.00
Ammonia	-35.50
Ethanol	78.40
Isopropyl Alchol	80.30
Mercury	356.90
Methane	-161.50
Methanol	66.00
Propane	-42.04
Sulfuric Acid	330.00
Water	100.00

type(_)

pandas.core.frame.DataFrame

Rows are extracted with the method loc, for example:

boiling.loc['Water']

F    100.0
C    212.0
Name: Water, dtype: float64

type(_)

pandas.core.series.Series

The row can also be returned as a DataFrame using the double bracket notation.

boiling.loc[['Water']] 

	F	C
Water	100.0	212.0

There is another way of extracting columns with a dot notation. It takes the flexibility of Python, pandas is also able to convert the columns as public attributes of the data frame object. Consider this example:

boiling.C

Acetylene          -119.00
Ammonia             -28.10
Ethanol             173.00
Isopropyl Alchol    177.00
Mercury             675.10
Methane            -258.69
Methanol            151.00
Propane             -43.67
Sulfuric Acid       626.00
Water               212.00
Name: C, dtype: float64

type(_)

pandas.core.series.Series

The (dot) notation only works if the names of the columns have no spaces, otherwise only the bracket column extraction applies.

df=pd.DataFrame({'case one': [1], 'case two': [2]})

df['case one']

0    1
Name: case one, dtype: int64

The location and extraction methods in Pandas are far more elaborated than just the examples above. Most data frames that are created in actual applications are not created from dictionaries but actual files.

Read data

It’s quite simple to load data from various file formats into a DataFrame. In the following examples, we’ll create data frames from several usual formats.

From CSV files

CSV stands for “comma-separated values”. Its data fields are most often separated, or delimited, by a comma. For example, let’s say you had a spreadsheet containing the following data.

CSV is a simple file format used to store tabular data, such as a spreadsheet or one table from a relational database. Files in the CSV format can be imported to and exported from programs that store data in tables, such as Microsoft Excel or OpenOffice Calc.

Being a text file, this format is not recommended when dealing with extremely large tables or more complex data structures, due to the natural limitations of the text format.

df = pd.read_csv('data/heart.csv')

This is a table downloaded from https://www.kaggle.com/ronitf/heart-disease-uci. The table contains several columns related to the presence of heart disease in a list of patients. In real applications, tables can be extremely large to be seen as complete. Pandas offer a few methods to get a quick overview of the contents of a DataFrame

df.head(10)

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	thal	target
0	63	1	3	145	233	1	0	150	0	2.3	0	1	1
1	37	1	2	130	250	0	1	187	0	3.5	0	2	1
2	41	0	1	130	204	0	0	172	0	1.4	2	2	1
3	56	1	1	120	236	0	1	178	0	0.8	2	2	1
4	57	0	0	120	354	0	1	163	1	0.6	2	2	1
5	57	1	0	140	192	0	1	148	0	0.4	1	1	1
6	56	0	1	140	294	0	0	153	0	1.3	1	2	1
7	44	1	1	120	263	0	1	173	0	0.0	2	3	1
8	52	1	2	172	199	1	1	162	0	0.5	2	3	1
9	57	1	2	150	168	0	1	174	0	1.6	2	2	1

df.tail(10)

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	ca	thal
293	67	1	2	152	212	0	0	150	0	0.8	1	0	3
294	44	1	0	120	169	0	1	144	1	2.8	0	0	1
295	63	1	0	140	187	0	0	144	1	4.0	2	2	3
296	63	0	0	124	197	0	1	136	1	0.0	1	0	2
297	59	1	0	164	176	1	0	90	0	1.0	1	2	1
298	57	0	0	140	241	0	1	123	1	0.2	1	0	3
299	45	1	3	110	264	0	1	132	0	1.2	1	0	3
300	68	1	0	144	193	1	1	141	0	3.4	1	2	3
301	57	1	0	130	131	0	1	115	1	1.2	1	1	3
302	57	0	1	130	236	0	0	174	0	0.0	1	1	2

df.shape

(303, 14)

df.size

df.loc[:,['age', 'sex']]

	age	sex
0	63	1
1	37	1
2	41	0
3	56	1
4	57	0
...	...	...
298	57	0
299	45	1
300	68	1
301	57	1
302	57	0

303 rows × 2 columns

# adding a new column
df["new column"]=None
df.head()

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	thal	target	new column
0	63	1	3	145	233	1	0	150	0	2.3	0	1	1	None
1	37	1	2	130	250	0	1	187	0	3.5	0	2	1	None
2	41	0	1	130	204	0	0	172	0	1.4	2	2	1	None
3	56	1	1	120	236	0	1	178	0	0.8	2	2	1	None
4	57	0	0	120	354	0	1	163	1	0.6	2	2	1	None

# dropping one column (also works with rows)
del df["new column"]
df.head()

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	thal	target
0	63	1	3	145	233	1	0	150	0	2.3	0	1	1
1	37	1	2	130	250	0	1	187	0	3.5	0	2	1
2	41	0	1	130	204	0	0	172	0	1.4	2	2	1
3	56	1	1	120	236	0	1	178	0	0.8	2	2	1
4	57	0	0	120	354	0	1	163	1	0.6	2	2	1

# Becareful if you make copies and modify the data
df1=df["age"]
df1 += 1
df.head()

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	thal	target
0	64	1	3	145	233	1	0	150	0	2.3	0	1	1
1	38	1	2	130	250	0	1	187	0	3.5	0	2	1
2	42	0	1	130	204	0	0	172	0	1.4	2	2	1
3	57	1	1	120	236	0	1	178	0	0.8	2	2	1
4	58	0	0	120	354	0	1	163	1	0.6	2	2	1

# if you are not in windows. you can communicate with the operating system
!cat data/heart.csv

age,sex,cp,trestbps,chol,fbs,restecg,thalach,exang,oldpeak,slope,ca,thal,target
63,1,3,145,233,1,0,150,0,2.3,0,0,1,1
37,1,2,130,250,0,1,187,0,3.5,0,0,2,1
41,0,1,130,204,0,0,172,0,1.4,2,0,2,1
56,1,1,120,236,0,1,178,0,0.8,2,0,2,1
57,0,0,120,354,0,1,163,1,0.6,2,0,2,1
57,1,0,140,192,0,1,148,0,0.4,1,0,1,1
56,0,1,140,294,0,0,153,0,1.3,1,0,2,1
44,1,1,120,263,0,1,173,0,0,2,0,3,1
52,1,2,172,199,1,1,162,0,0.5,2,0,3,1
57,1,2,150,168,0,1,174,0,1.6,2,0,2,1
54,1,0,140,239,0,1,160,0,1.2,2,0,2,1
48,0,2,130,275,0,1,139,0,0.2,2,0,2,1
49,1,1,130,266,0,1,171,0,0.6,2,0,2,1
64,1,3,110,211,0,0,144,1,1.8,1,0,2,1
58,0,3,150,283,1,0,162,0,1,2,0,2,1
50,0,2,120,219,0,1,158,0,1.6,1,0,2,1
58,0,2,120,340,0,1,172,0,0,2,0,2,1
66,0,3,150,226,0,1,114,0,2.6,0,0,2,1
43,1,0,150,247,0,1,171,0,1.5,2,0,2,1
69,0,3,140,239,0,1,151,0,1.8,2,2,2,1
59,1,0,135,234,0,1,161,0,0.5,1,0,3,1
44,1,2,130,233,0,1,179,1,0.4,2,0,2,1
42,1,0,140,226,0,1,178,0,0,2,0,2,1
61,1,2,150,243,1,1,137,1,1,1,0,2,1
40,1,3,140,199,0,1,178,1,1.4,2,0,3,1
71,0,1,160,302,0,1,162,0,0.4,2,2,2,1
59,1,2,150,212,1,1,157,0,1.6,2,0,2,1
51,1,2,110,175,0,1,123,0,0.6,2,0,2,1
65,0,2,140,417,1,0,157,0,0.8,2,1,2,1
53,1,2,130,197,1,0,152,0,1.2,0,0,2,1
41,0,1,105,198,0,1,168,0,0,2,1,2,1
65,1,0,120,177,0,1,140,0,0.4,2,0,3,1
44,1,1,130,219,0,0,188,0,0,2,0,2,1
54,1,2,125,273,0,0,152,0,0.5,0,1,2,1
51,1,3,125,213,0,0,125,1,1.4,2,1,2,1
46,0,2,142,177,0,0,160,1,1.4,0,0,2,1
54,0,2,135,304,1,1,170,0,0,2,0,2,1
54,1,2,150,232,0,0,165,0,1.6,2,0,3,1
65,0,2,155,269,0,1,148,0,0.8,2,0,2,1
65,0,2,160,360,0,0,151,0,0.8,2,0,2,1
51,0,2,140,308,0,0,142,0,1.5,2,1,2,1
48,1,1,130,245,0,0,180,0,0.2,1,0,2,1
45,1,0,104,208,0,0,148,1,3,1,0,2,1
53,0,0,130,264,0,0,143,0,0.4,1,0,2,1
39,1,2,140,321,0,0,182,0,0,2,0,2,1
52,1,1,120,325,0,1,172,0,0.2,2,0,2,1
44,1,2,140,235,0,0,180,0,0,2,0,2,1
47,1,2,138,257,0,0,156,0,0,2,0,2,1
53,0,2,128,216,0,0,115,0,0,2,0,0,1
53,0,0,138,234,0,0,160,0,0,2,0,2,1
51,0,2,130,256,0,0,149,0,0.5,2,0,2,1
66,1,0,120,302,0,0,151,0,0.4,1,0,2,1
62,1,2,130,231,0,1,146,0,1.8,1,3,3,1
44,0,2,108,141,0,1,175,0,0.6,1,0,2,1
63,0,2,135,252,0,0,172,0,0,2,0,2,1
52,1,1,134,201,0,1,158,0,0.8,2,1,2,1
48,1,0,122,222,0,0,186,0,0,2,0,2,1
45,1,0,115,260,0,0,185,0,0,2,0,2,1
34,1,3,118,182,0,0,174,0,0,2,0,2,1
57,0,0,128,303,0,0,159,0,0,2,1,2,1
71,0,2,110,265,1,0,130,0,0,2,1,2,1
54,1,1,108,309,0,1,156,0,0,2,0,3,1
52,1,3,118,186,0,0,190,0,0,1,0,1,1
41,1,1,135,203,0,1,132,0,0,1,0,1,1
58,1,2,140,211,1,0,165,0,0,2,0,2,1
35,0,0,138,183,0,1,182,0,1.4,2,0,2,1
51,1,2,100,222,0,1,143,1,1.2,1,0,2,1
45,0,1,130,234,0,0,175,0,0.6,1,0,2,1
44,1,1,120,220,0,1,170,0,0,2,0,2,1
62,0,0,124,209,0,1,163,0,0,2,0,2,1
54,1,2,120,258,0,0,147,0,0.4,1,0,3,1
51,1,2,94,227,0,1,154,1,0,2,1,3,1
29,1,1,130,204,0,0,202,0,0,2,0,2,1
51,1,0,140,261,0,0,186,1,0,2,0,2,1
43,0,2,122,213,0,1,165,0,0.2,1,0,2,1
55,0,1,135,250,0,0,161,0,1.4,1,0,2,1
51,1,2,125,245,1,0,166,0,2.4,1,0,2,1
59,1,1,140,221,0,1,164,1,0,2,0,2,1
52,1,1,128,205,1,1,184,0,0,2,0,2,1
58,1,2,105,240,0,0,154,1,0.6,1,0,3,1
41,1,2,112,250,0,1,179,0,0,2,0,2,1
45,1,1,128,308,0,0,170,0,0,2,0,2,1
60,0,2,102,318,0,1,160,0,0,2,1,2,1
52,1,3,152,298,1,1,178,0,1.2,1,0,3,1
42,0,0,102,265,0,0,122,0,0.6,1,0,2,1
67,0,2,115,564,0,0,160,0,1.6,1,0,3,1
68,1,2,118,277,0,1,151,0,1,2,1,3,1
46,1,1,101,197,1,1,156,0,0,2,0,3,1
54,0,2,110,214,0,1,158,0,1.6,1,0,2,1
58,0,0,100,248,0,0,122,0,1,1,0,2,1
48,1,2,124,255,1,1,175,0,0,2,2,2,1
57,1,0,132,207,0,1,168,1,0,2,0,3,1
52,1,2,138,223,0,1,169,0,0,2,4,2,1
54,0,1,132,288,1,0,159,1,0,2,1,2,1
45,0,1,112,160,0,1,138,0,0,1,0,2,1
53,1,0,142,226,0,0,111,1,0,2,0,3,1
62,0,0,140,394,0,0,157,0,1.2,1,0,2,1
52,1,0,108,233,1,1,147,0,0.1,2,3,3,1
43,1,2,130,315,0,1,162,0,1.9,2,1,2,1
53,1,2,130,246,1,0,173,0,0,2,3,2,1
42,1,3,148,244,0,0,178,0,0.8,2,2,2,1
59,1,3,178,270,0,0,145,0,4.2,0,0,3,1
63,0,1,140,195,0,1,179,0,0,2,2,2,1
42,1,2,120,240,1,1,194,0,0.8,0,0,3,1
50,1,2,129,196,0,1,163,0,0,2,0,2,1
68,0,2,120,211,0,0,115,0,1.5,1,0,2,1
69,1,3,160,234,1,0,131,0,0.1,1,1,2,1
45,0,0,138,236,0,0,152,1,0.2,1,0,2,1
50,0,1,120,244,0,1,162,0,1.1,2,0,2,1
50,0,0,110,254,0,0,159,0,0,2,0,2,1
64,0,0,180,325,0,1,154,1,0,2,0,2,1
57,1,2,150,126,1,1,173,0,0.2,2,1,3,1
64,0,2,140,313,0,1,133,0,0.2,2,0,3,1
43,1,0,110,211,0,1,161,0,0,2,0,3,1
55,1,1,130,262,0,1,155,0,0,2,0,2,1
37,0,2,120,215,0,1,170,0,0,2,0,2,1
41,1,2,130,214,0,0,168,0,2,1,0,2,1
56,1,3,120,193,0,0,162,0,1.9,1,0,3,1
46,0,1,105,204,0,1,172,0,0,2,0,2,1
46,0,0,138,243,0,0,152,1,0,1,0,2,1
64,0,0,130,303,0,1,122,0,2,1,2,2,1
59,1,0,138,271,0,0,182,0,0,2,0,2,1
41,0,2,112,268,0,0,172,1,0,2,0,2,1
54,0,2,108,267,0,0,167,0,0,2,0,2,1
39,0,2,94,199,0,1,179,0,0,2,0,2,1
34,0,1,118,210,0,1,192,0,0.7,2,0,2,1
47,1,0,112,204,0,1,143,0,0.1,2,0,2,1
67,0,2,152,277,0,1,172,0,0,2,1,2,1
52,0,2,136,196,0,0,169,0,0.1,1,0,2,1
74,0,1,120,269,0,0,121,1,0.2,2,1,2,1
54,0,2,160,201,0,1,163,0,0,2,1,2,1
49,0,1,134,271,0,1,162,0,0,1,0,2,1
42,1,1,120,295,0,1,162,0,0,2,0,2,1
41,1,1,110,235,0,1,153,0,0,2,0,2,1
41,0,1,126,306,0,1,163,0,0,2,0,2,1
49,0,0,130,269,0,1,163,0,0,2,0,2,1
60,0,2,120,178,1,1,96,0,0,2,0,2,1
62,1,1,128,208,1,0,140,0,0,2,0,2,1
57,1,0,110,201,0,1,126,1,1.5,1,0,1,1
64,1,0,128,263,0,1,105,1,0.2,1,1,3,1
51,0,2,120,295,0,0,157,0,0.6,2,0,2,1
43,1,0,115,303,0,1,181,0,1.2,1,0,2,1
42,0,2,120,209,0,1,173,0,0,1,0,2,1
67,0,0,106,223,0,1,142,0,0.3,2,2,2,1
76,0,2,140,197,0,2,116,0,1.1,1,0,2,1
70,1,1,156,245,0,0,143,0,0,2,0,2,1
44,0,2,118,242,0,1,149,0,0.3,1,1,2,1
60,0,3,150,240,0,1,171,0,0.9,2,0,2,1
44,1,2,120,226,0,1,169,0,0,2,0,2,1
42,1,2,130,180,0,1,150,0,0,2,0,2,1
66,1,0,160,228,0,0,138,0,2.3,2,0,1,1
71,0,0,112,149,0,1,125,0,1.6,1,0,2,1
64,1,3,170,227,0,0,155,0,0.6,1,0,3,1
66,0,2,146,278,0,0,152,0,0,1,1,2,1
39,0,2,138,220,0,1,152,0,0,1,0,2,1
58,0,0,130,197,0,1,131,0,0.6,1,0,2,1
47,1,2,130,253,0,1,179,0,0,2,0,2,1
35,1,1,122,192,0,1,174,0,0,2,0,2,1
58,1,1,125,220,0,1,144,0,0.4,1,4,3,1
56,1,1,130,221,0,0,163,0,0,2,0,3,1
56,1,1,120,240,0,1,169,0,0,0,0,2,1
55,0,1,132,342,0,1,166,0,1.2,2,0,2,1
41,1,1,120,157,0,1,182,0,0,2,0,2,1
38,1,2,138,175,0,1,173,0,0,2,4,2,1
38,1,2,138,175,0,1,173,0,0,2,4,2,1
67,1,0,160,286,0,0,108,1,1.5,1,3,2,0
67,1,0,120,229,0,0,129,1,2.6,1,2,3,0
62,0,0,140,268,0,0,160,0,3.6,0,2,2,0
63,1,0,130,254,0,0,147,0,1.4,1,1,3,0
53,1,0,140,203,1,0,155,1,3.1,0,0,3,0
56,1,2,130,256,1,0,142,1,0.6,1,1,1,0
48,1,1,110,229,0,1,168,0,1,0,0,3,0
58,1,1,120,284,0,0,160,0,1.8,1,0,2,0
58,1,2,132,224,0,0,173,0,3.2,2,2,3,0
60,1,0,130,206,0,0,132,1,2.4,1,2,3,0
40,1,0,110,167,0,0,114,1,2,1,0,3,0
60,1,0,117,230,1,1,160,1,1.4,2,2,3,0
64,1,2,140,335,0,1,158,0,0,2,0,2,0
43,1,0,120,177,0,0,120,1,2.5,1,0,3,0
57,1,0,150,276,0,0,112,1,0.6,1,1,1,0
55,1,0,132,353,0,1,132,1,1.2,1,1,3,0
65,0,0,150,225,0,0,114,0,1,1,3,3,0
61,0,0,130,330,0,0,169,0,0,2,0,2,0
58,1,2,112,230,0,0,165,0,2.5,1,1,3,0
50,1,0,150,243,0,0,128,0,2.6,1,0,3,0
44,1,0,112,290,0,0,153,0,0,2,1,2,0
60,1,0,130,253,0,1,144,1,1.4,2,1,3,0
54,1,0,124,266,0,0,109,1,2.2,1,1,3,0
50,1,2,140,233,0,1,163,0,0.6,1,1,3,0
41,1,0,110,172,0,0,158,0,0,2,0,3,0
51,0,0,130,305,0,1,142,1,1.2,1,0,3,0
58,1,0,128,216,0,0,131,1,2.2,1,3,3,0
54,1,0,120,188,0,1,113,0,1.4,1,1,3,0
60,1,0,145,282,0,0,142,1,2.8,1,2,3,0
60,1,2,140,185,0,0,155,0,3,1,0,2,0
59,1,0,170,326,0,0,140,1,3.4,0,0,3,0
46,1,2,150,231,0,1,147,0,3.6,1,0,2,0
67,1,0,125,254,1,1,163,0,0.2,1,2,3,0
62,1,0,120,267,0,1,99,1,1.8,1,2,3,0
65,1,0,110,248,0,0,158,0,0.6,2,2,1,0
44,1,0,110,197,0,0,177,0,0,2,1,2,0
60,1,0,125,258,0,0,141,1,2.8,1,1,3,0
58,1,0,150,270,0,0,111,1,0.8,2,0,3,0
68,1,2,180,274,1,0,150,1,1.6,1,0,3,0
62,0,0,160,164,0,0,145,0,6.2,0,3,3,0
52,1,0,128,255,0,1,161,1,0,2,1,3,0
59,1,0,110,239,0,0,142,1,1.2,1,1,3,0
60,0,0,150,258,0,0,157,0,2.6,1,2,3,0
49,1,2,120,188,0,1,139,0,2,1,3,3,0
59,1,0,140,177,0,1,162,1,0,2,1,3,0
57,1,2,128,229,0,0,150,0,0.4,1,1,3,0
61,1,0,120,260,0,1,140,1,3.6,1,1,3,0
39,1,0,118,219,0,1,140,0,1.2,1,0,3,0
61,0,0,145,307,0,0,146,1,1,1,0,3,0
56,1,0,125,249,1,0,144,1,1.2,1,1,2,0
43,0,0,132,341,1,0,136,1,3,1,0,3,0
62,0,2,130,263,0,1,97,0,1.2,1,1,3,0
63,1,0,130,330,1,0,132,1,1.8,2,3,3,0
65,1,0,135,254,0,0,127,0,2.8,1,1,3,0
48,1,0,130,256,1,0,150,1,0,2,2,3,0
63,0,0,150,407,0,0,154,0,4,1,3,3,0
55,1,0,140,217,0,1,111,1,5.6,0,0,3,0
65,1,3,138,282,1,0,174,0,1.4,1,1,2,0
56,0,0,200,288,1,0,133,1,4,0,2,3,0
54,1,0,110,239,0,1,126,1,2.8,1,1,3,0
70,1,0,145,174,0,1,125,1,2.6,0,0,3,0
62,1,1,120,281,0,0,103,0,1.4,1,1,3,0
35,1,0,120,198,0,1,130,1,1.6,1,0,3,0
59,1,3,170,288,0,0,159,0,0.2,1,0,3,0
64,1,2,125,309,0,1,131,1,1.8,1,0,3,0
47,1,2,108,243,0,1,152,0,0,2,0,2,0
57,1,0,165,289,1,0,124,0,1,1,3,3,0
55,1,0,160,289,0,0,145,1,0.8,1,1,3,0
64,1,0,120,246,0,0,96,1,2.2,0,1,2,0
70,1,0,130,322,0,0,109,0,2.4,1,3,2,0
51,1,0,140,299,0,1,173,1,1.6,2,0,3,0
58,1,0,125,300,0,0,171,0,0,2,2,3,0
60,1,0,140,293,0,0,170,0,1.2,1,2,3,0
77,1,0,125,304,0,0,162,1,0,2,3,2,0
35,1,0,126,282,0,0,156,1,0,2,0,3,0
70,1,2,160,269,0,1,112,1,2.9,1,1,3,0
59,0,0,174,249,0,1,143,1,0,1,0,2,0
64,1,0,145,212,0,0,132,0,2,1,2,1,0
57,1,0,152,274,0,1,88,1,1.2,1,1,3,0
56,1,0,132,184,0,0,105,1,2.1,1,1,1,0
48,1,0,124,274,0,0,166,0,0.5,1,0,3,0
56,0,0,134,409,0,0,150,1,1.9,1,2,3,0
66,1,1,160,246,0,1,120,1,0,1,3,1,0
54,1,1,192,283,0,0,195,0,0,2,1,3,0
69,1,2,140,254,0,0,146,0,2,1,3,3,0
51,1,0,140,298,0,1,122,1,4.2,1,3,3,0
43,1,0,132,247,1,0,143,1,0.1,1,4,3,0
62,0,0,138,294,1,1,106,0,1.9,1,3,2,0
67,1,0,100,299,0,0,125,1,0.9,1,2,2,0
59,1,3,160,273,0,0,125,0,0,2,0,2,0
45,1,0,142,309,0,0,147,1,0,1,3,3,0
58,1,0,128,259,0,0,130,1,3,1,2,3,0
50,1,0,144,200,0,0,126,1,0.9,1,0,3,0
62,0,0,150,244,0,1,154,1,1.4,1,0,2,0
38,1,3,120,231,0,1,182,1,3.8,1,0,3,0
66,0,0,178,228,1,1,165,1,1,1,2,3,0
52,1,0,112,230,0,1,160,0,0,2,1,2,0
53,1,0,123,282,0,1,95,1,2,1,2,3,0
63,0,0,108,269,0,1,169,1,1.8,1,2,2,0
54,1,0,110,206,0,0,108,1,0,1,1,2,0
66,1,0,112,212,0,0,132,1,0.1,2,1,2,0
55,0,0,180,327,0,2,117,1,3.4,1,0,2,0
49,1,2,118,149,0,0,126,0,0.8,2,3,2,0
54,1,0,122,286,0,0,116,1,3.2,1,2,2,0
56,1,0,130,283,1,0,103,1,1.6,0,0,3,0
46,1,0,120,249,0,0,144,0,0.8,2,0,3,0
61,1,3,134,234,0,1,145,0,2.6,1,2,2,0
67,1,0,120,237,0,1,71,0,1,1,0,2,0
58,1,0,100,234,0,1,156,0,0.1,2,1,3,0
47,1,0,110,275,0,0,118,1,1,1,1,2,0
52,1,0,125,212,0,1,168,0,1,2,2,3,0
58,1,0,146,218,0,1,105,0,2,1,1,3,0
57,1,1,124,261,0,1,141,0,0.3,2,0,3,0
58,0,1,136,319,1,0,152,0,0,2,2,2,0
61,1,0,138,166,0,0,125,1,3.6,1,1,2,0
42,1,0,136,315,0,1,125,1,1.8,1,0,1,0
52,1,0,128,204,1,1,156,1,1,1,0,0,0
59,1,2,126,218,1,1,134,0,2.2,1,1,1,0
40,1,0,152,223,0,1,181,0,0,2,0,3,0
61,1,0,140,207,0,0,138,1,1.9,2,1,3,0
46,1,0,140,311,0,1,120,1,1.8,1,2,3,0
59,1,3,134,204,0,1,162,0,0.8,2,2,2,0
57,1,1,154,232,0,0,164,0,0,2,1,2,0
57,1,0,110,335,0,1,143,1,3,1,1,3,0
55,0,0,128,205,0,2,130,1,2,1,1,3,0
61,1,0,148,203,0,1,161,0,0,2,1,3,0
58,1,0,114,318,0,2,140,0,4.4,0,3,1,0
58,0,0,170,225,1,0,146,1,2.8,1,2,1,0
67,1,2,152,212,0,0,150,0,0.8,1,0,3,0
44,1,0,120,169,0,1,144,1,2.8,0,0,1,0
63,1,0,140,187,0,0,144,1,4,2,2,3,0
63,0,0,124,197,0,1,136,1,0,1,0,2,0
59,1,0,164,176,1,0,90,0,1,1,2,1,0
57,0,0,140,241,0,1,123,1,0.2,1,0,3,0
45,1,3,110,264,0,1,132,0,1.2,1,0,3,0
68,1,0,144,193,1,1,141,0,3.4,1,2,3,0
57,1,0,130,131,0,1,115,1,1.2,1,1,3,0
57,0,1,130,236,0,0,174,0,0,1,1,2,0

# if you want to read the CSV file but you want to skip the first 3 lines
df = pd.read_csv('data/heart.csv',skiprows=3)
df.head()

	41	0	1	130	204	0.2	172	0.3	1.4	2	2.1	1.1
0	56	1	1	120	236	1	178	0	0.8	2	2	1
1	57	0	0	120	354	1	163	1	0.6	2	2	1
2	57	1	0	140	192	1	148	0	0.4	1	1	1
3	56	0	1	140	294	0	153	0	1.3	1	2	1
4	44	1	1	120	263	1	173	0	0.0	2	3	1

# if we want to use the first column as the index
df = pd.read_csv('data/heart.csv',index_col=0,skiprows=3)
df.head()

	0	1	130	204	0.1	0.2	172	0.3	1.4	2	0.4	2.1	1.1
41
56	1	1	120	236	0	1	178	0	0.8	2	0	2	1
57	0	0	120	354	0	1	163	1	0.6	2	0	2	1
57	1	0	140	192	0	1	148	0	0.4	1	0	1	1
56	0	1	140	294	0	0	153	0	1.3	1	0	2	1
44	1	1	120	263	0	1	173	0	0.0	2	0	3	1

From JSON Files

JSON (JavaScript Object Notation) is a lightweight data-interchange format. It is easy for humans to read and write. It is easy for machines to parse and generate. It is based on a subset of the JavaScript Programming Language, Standard ECMA-262 3rd Edition - December 1999. JSON is a text format that is completely language-independent but uses conventions that are familiar to programmers of the C-family of languages, including C, C++, C#, Java, JavaScript, Perl, Python, and many others. These properties make JSON an ideal data-interchange language.

JSON is particularly useful for Data Analysis on Python as the JSON parser is part of the Standard Library and its format looks very similar to Python dictionaries. However, notice that a JSON file or JSON string is just a set of bytes that can be read as text. A python dictionary is a complete data structure. Other differences between JSON strings and dictionaries are:

Python’s dictionary key can hash any object, and JSON can only be a string.
The Python dict string can be created with single or double quotation marks. When represented on the screen, single quotes are used, however, a JSON string enforces double quotation marks.
You can nest tuple in Python dict. JSON can only use an array.

In practice, that means that a JSON file can always be converted into a Python dictionary, but the reverse is not always true.

df=pd.read_json("data/heart.json")

From SQLite Databases

SQLite is a C-language library that implements a small, fast, self-contained, high-reliability, full-featured, SQL database engine. SQLite is the most used database engine in the world. In practice, SQLite is a serverless SQL database in a file.

import sqlite3

con = sqlite3.connect("data/heart.db")

df = pd.read_sql_query("SELECT * FROM heart", con)

df.head()

	index	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	thal	target
0	0	63	1	3	145	233	1	0	150	0	2.3	0	1	1
1	1	37	1	2	130	250	0	1	187	0	3.5	0	2	1
2	2	41	0	1	130	204	0	0	172	0	1.4	2	2	1
3	3	56	1	1	120	236	0	1	178	0	0.8	2	2	1
4	4	57	0	0	120	354	0	1	163	1	0.6	2	2	1

From Excel files

Pandas also support reading Excel files, however, to read files from recent versions of Excel. You need to install the xlrd package

#pip install xlrd

If you are using conda, the package can be installed with:

#conda install xlrd

After the package has been installed, pandas can read the Excel files version >= 2.0

df=pd.read_excel('data/2018_all_indicators.xlsx')

From other formats

Pandas is very versatile in accepting a variety of formats: STATA, SAS, HDF5 files. See https://pandas.pydata.org/pandas-docs/stable/reference/io.html for more information on the multiple formats supported.

Write DataFrames

Pandas also offers the ability to store resulting DataFrames back into several formats. Consider this example:

heart = pd.read_csv('data/heart.csv')

Saving the data frame in those formats execute:

if os.path.isfile("new_heart.db"):
    os.remove("new_heart.db")

heart.to_csv('new_heart.csv')

heart.to_json('new_heart.json')

con = sqlite3.connect("new_heart.db")
heart.to_sql('heart', con)

os.remove("new_heart.csv")
os.remove("new_heart.json")
os.remove("new_heart.db")

View the data

We already saw how to use tail and head to get a glimpse into the initial and final rows. The default is 5 rows, but the value can be modified.

heart.head(3)

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	oldpeak	slope	thal	target
0	63	1	3	145	233	1	0	150	2.3	0	1	1
1	37	1	2	130	250	0	1	187	3.5	0	2	1
2	41	0	1	130	204	0	0	172	1.4	2	2	1

heart.tail(3)

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	ca	thal
300	68	1	0	144	193	1	1	141	0	3.4	1	2	3
301	57	1	0	130	131	0	1	115	1	1.2	1	1	3
302	57	0	1	130	236	0	0	174	0	0.0	1	1	2

Another method is info to see the columns and the type of values stored on them. In general, Pandas try to associate a numerical value when possible. However, it will revert into datatype object when mixed values are found.

heart.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 303 entries, 0 to 302
Data columns (total 14 columns):
 #   Column    Non-Null Count  Dtype  
---  ------    --------------  -----  
 0   age       303 non-null    int64  
 1   sex       303 non-null    int64  
 2   cp        303 non-null    int64  
 3   trestbps  303 non-null    int64  
 4   chol      303 non-null    int64  
 5   fbs       303 non-null    int64  
 6   restecg   303 non-null    int64  
 7   thalach   303 non-null    int64  
 8   exang     303 non-null    int64  
 9   oldpeak   303 non-null    float64
 10  slope     303 non-null    int64  
 11  ca        303 non-null    int64  
 12  thal      303 non-null    int64  
 13  target    303 non-null    int64  
dtypes: float64(1), int64(13)
memory usage: 33.3 KB

In this particular case, the table is rather clean, with all columns populated. It is often the case where some columns have missing data, we will deal with them in another example.

Another way to query the database and mask some of the results can be by using boolean operations. Let’s see some examples

# here we select all people with heart conditions and older than 50
#print(heart.isna)
only50 = heart.where(heart['age'] > 50)
print(only50.head())
#only people that has the condition has values, the other has NaN as entries
#NaN are not counted or used in statistical analysis of the data frame. 
count1=only50['age'].count()
count2=heart['age'].count()
print('Values with NoNaNs in only50 ',count1,' and in the whole database', count2)
only50real=only50.dropna()
print(only50real.head())
# we can delete all rows with NaN as

    age  sex   cp  trestbps   chol  fbs  restecg  thalach  exang  oldpeak  \
63.0  1.0  3.0     145.0  233.0  1.0      0.0    150.0    0.0      2.3   
 NaN  NaN  NaN       NaN    NaN  NaN      NaN      NaN    NaN      NaN   
 NaN  NaN  NaN       NaN    NaN  NaN      NaN      NaN    NaN      NaN   
56.0  1.0  1.0     120.0  236.0  0.0      1.0    178.0    0.0      0.8   
57.0  0.0  0.0     120.0  354.0  0.0      1.0    163.0    1.0      0.6   

   slope   ca  thal  target  
  0.0  0.0   1.0     1.0  
  NaN  NaN   NaN     NaN  
  NaN  NaN   NaN     NaN  
  2.0  0.0   2.0     1.0  
  2.0  0.0   2.0     1.0  
Values with NoNaNs in only50  208  and in the whole database 303
    age  sex   cp  trestbps   chol  fbs  restecg  thalach  exang  oldpeak  \
63.0  1.0  3.0     145.0  233.0  1.0      0.0    150.0    0.0      2.3   
56.0  1.0  1.0     120.0  236.0  0.0      1.0    178.0    0.0      0.8   
57.0  0.0  0.0     120.0  354.0  0.0      1.0    163.0    1.0      0.6   
57.0  1.0  0.0     140.0  192.0  0.0      1.0    148.0    0.0      0.4   
56.0  0.0  1.0     140.0  294.0  0.0      0.0    153.0    0.0      1.3   

   slope   ca  thal  target  
  0.0  0.0   1.0     1.0  
  2.0  0.0   2.0     1.0  
  2.0  0.0   2.0     1.0  
  1.0  0.0   1.0     1.0  
  1.0  0.0   2.0     1.0  

# we can avoid all this problem is we use
only50 = heart[heart['age']>50]
print(only50.head())
# but now we can do it more complex, for example, people older than 50 with cholesterol larger than 150
only50 = heart[(heart['age']>50) & (heart['chol'] > 150)]

   age  sex  cp  trestbps  chol  fbs  restecg  thalach  exang  oldpeak  slope  \
 63    1   3       145   233    1        0      150      0      2.3      0   
 56    1   1       120   236    0        1      178      0      0.8      2   
 57    0   0       120   354    0        1      163      1      0.6      2   
 57    1   0       140   192    0        1      148      0      0.4      1   
 56    0   1       140   294    0        0      153      0      1.3      1   

   ca  thal  target  
 0     1       1  
 0     2       1  
 0     2       1  
 0     1       1  
 0     2       1  

#we can also order things promoting a column to be the index
heart1=heart.set_index('age')
print(heart1.head())
# we can also come back to the original index and move the existing index to a new column
heart1=heart1.reset_index()
print(heart1.head())
# for binary we can alw

     sex  cp  trestbps  chol  fbs  restecg  thalach  exang  oldpeak  slope  \
age                                                                          
   1   3       145   233    1        0      150      0      2.3      0   
   1   2       130   250    0        1      187      0      3.5      0   
   0   1       130   204    0        0      172      0      1.4      2   
   1   1       120   236    0        1      178      0      0.8      2   
   0   0       120   354    0        1      163      1      0.6      2   

     ca  thal  target  
age                    
  0     1       1  
  0     2       1  
  0     2       1  
  0     2       1  
  0     2       1  
   age  sex  cp  trestbps  chol  fbs  restecg  thalach  exang  oldpeak  slope  \
 63    1   3       145   233    1        0      150      0      2.3      0   
 37    1   2       130   250    0        1      187      0      3.5      0   
 41    0   1       130   204    0        0      172      0      1.4      2   
 56    1   1       120   236    0        1      178      0      0.8      2   
 57    0   0       120   354    0        1      163      1      0.6      2   

   ca  thal  target  
 0     1       1  
 0     2       1  
 0     2       1  
 0     2       1  
 0     2       1  

# There is a cool idea in Pandas which is hierarchical indexes.. for example, 
case1 = pd.Series({'Date': '2020-05-01','Class': 'class 1','Value': 1})
case2 = pd.Series({'Date': '2020-05-01','Class': 'class 2','Value': 2})
case3 = pd.Series({'Date': '2020-05-02','Class': 'class 1','Value': 3})
case4 = pd.Series({'Date': '2020-05-03','Class': 'class 1','Value': 4})
case5 = pd.Series({'Date': '2020-05-03','Class': 'class 2','Value': 5})
case6 = pd.Series({'Date': '2020-05-04','Class': 'class 1','Value': 6})


df=pd.DataFrame([case1,case2,case3,case4,case5,case6])
print(df.head())

         Date    Class  Value
2020-05-01  class 1      1
2020-05-01  class 2      2
2020-05-02  class 1      3
2020-05-03  class 1      4
2020-05-03  class 2      5

df = df.set_index(['Date', 'Class'])
print(df.head())

                    Value
Date       Class         
2020-05-01 class 1      1
           class 2      2
2020-05-02 class 1      3
2020-05-03 class 1      4
           class 2      5

Checking and removing duplicates

Another important check to perform on DataFrames is search for duplicated rows. Let’s continue using the ‘hearth’ data frame and search duplicated rows.

heart.duplicated()

    False
    False
    False
    False
    False
       ...  
  False
  False
  False
  False
  False
Length: 303, dtype: bool

The answer is a pandas series indicating if the row is duplicated or not. Let’s see the duplicates:

heart[heart.duplicated(keep=False)]

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	ca	thal	target
163	38	1	2	138	175	0	1	173	0	0.0	2	4	2	1
164	38	1	2	138	175	0	1	173	0	0.0	2	4	2	1

Two contiguous rows are identical. Most likely a human mistake entering the values. We can create a new DataFrame with one of those rows removed

heart_nodup = heart.drop_duplicates()

heart_nodup.shape

(302, 14)

Compare with the original DataFrame:

heart.shape

(303, 14)

Dataset Merging

# There is a cool idea in Pandas which is hierarchical indexes.. for example, 
case1 = pd.Series({'Date': '2020-05-01','Class': 'class 1','Value': 1})
case2 = pd.Series({'Date': '2020-05-01','Class': 'class 2','Value': 2})
case3 = pd.Series({'Date': '2020-05-02','Class': 'class 1','Value': 3})
case4 = pd.Series({'Date': '2020-05-03','Class': 'class 1','Value': 4})
case5 = pd.Series({'Date': '2020-05-03','Class': 'class 2','Value': 5})
case6 = pd.Series({'Date': '2020-05-04','Class': 'class 1','Value': 6})


df=pd.DataFrame([case1,case2,case3,case4,case5,case6])
print(df.head())

         Date    Class  Value
2020-05-01  class 1      1
2020-05-01  class 2      2
2020-05-02  class 1      3
2020-05-03  class 1      4
2020-05-03  class 2      5

df['Book']=['book 1','book 2','book 3','book 4','book 5','book 6']
print(df.head())

         Date    Class  Value    Book
2020-05-01  class 1      1  book 1
2020-05-01  class 2      2  book 2
2020-05-02  class 1      3  book 3
2020-05-03  class 1      4  book 4
2020-05-03  class 2      5  book 5

# A different method use index as the criteria
newdf=df.reset_index()
newdf['New Book']=pd.Series({1:'New Book 1',4:'New Book 4'})
print(newdf.head())

   index        Date    Class  Value    Book    New Book
    0  2020-05-01  class 1      1  book 1         NaN
    1  2020-05-01  class 2      2  book 2  New Book 1
    2  2020-05-02  class 1      3  book 3         NaN
    3  2020-05-03  class 1      4  book 4         NaN
    4  2020-05-03  class 2      5  book 5  New Book 4

# Let see how Merge works

Plotting

%matplotlib inline
heart['age'].plot.hist(bins=20);

png

import seaborn as sns

h4=heart[['age', 'trestbps', 'chol', 'thalach']]
goal=[ 'no heart disease' if x==1 else 'heart disease' for x in heart['target'] ]
h5=h4.join(pd.DataFrame(goal, columns=['goal']))

import matplotlib.pyplot as plt

g = sns.PairGrid(h5, hue="goal")
g.map_diag(plt.hist)
g.map_offdiag(plt.scatter)
g.add_legend();

png

Acknowledgments and References

Changes to the original tutorial include strict Python 3 formats and a split of the material to fit a series of lessons on Python Programming for WVU’s faculty and graduate students.

The support of the National Science Foundation and the US Department of Energy under projects: DMREF-NSF 1434897, NSF OAC-1740111 and DOE DE-SC0016176 is recognized.

Back of the Book

plt.figure(figsize=(3,3))
n = chapter_number
maxt=(2*(n-1)+3)*np.pi/2
t = np.linspace(np.pi/2, maxt, 1000)
tt= 1.0/(t+0.01)
x = (maxt-t)*np.cos(t)**3
y = t*np.sqrt(np.abs(np.cos(t))) + np.sin(0.3*t)*np.cos(2*t)
plt.plot(x, y, c="green")
plt.axis('off');

png

end = time.time()
print(f'Chapter {chapter_number} run in {int(end - start):d} seconds')

Chapter 7 run in 32 seconds

Key Points

numpy is the standard de-facto for numerical calculations at large scale in Python

Final remarks

Overview

Teaching: min
Exercises: min

Topics

Objectives

Use the break layout for placeholder episodes representing coffee breaks and lunches. These episodes do not have exercises, questions, objectives, or key points in their metadata, but must have a “break” field to show how long the break is (in minutes).

Key Points

Workload Manager: Slurm

Overview

Teaching: 60 min
Exercises: 30 min

Topics

What is a resource manager, a scheduler, and a workload manager?

How do we submit a job on an HPC cluster?

Objectives

Submit a job and have it completed successfully.

Understand how to make resource requests.

Submit an interactive job.

Learn the most frequently used SLURM commands

Imagine for a moment that you need to execute a large simulation and all that you have is the computer that is in front of you. You will initiate the simulation by launching the program that will compute it. You ajust the parameters to avoid overloading the machine with more concurrent operations than the machine can process efficiently. It is possible that you cannot do anything else with the computer until the simulation is finished.

Changing the situation a bit, now you have several computers at your disposal and you have many simulations to do, maybe the same simulation but under different physical conditions. You will have to connect to each computer to start the simulation and periodically monitor the computers to check if some of them have finished and its ready to run a new simulation.

Moving to an even more complex scenario. Consider the case of several users, each wanting to run many simulations like yours and having a number of computers capable of runing all those simulations. Coordinating all the work and all the executions could be a daunting task that can be solved if a program could take care or mapping all the jobs from all the users to the available resources and monitoring when one computer can take another job.

All what we have described is the work of two programs, a resource manager in charge of monitoring the state of a pool of computers and a scheduler that will assign jobs to the different machines as fairly as possible for all the users in the cluster. In the case of our cluster those two roles are managed by a single software called Slurm and the integration of the resource manager, scheduler with the addition and accounting and other roles makes Slurm to be called a Workload Manager.

An HPC system such as Thorny Flat or Dolly Sods has tenths nodes and more than 100 users. How do we decide who gets what and when? How do we ensure that a task is run with the resources it needs? This job is handled by a special piece of software called the scheduler. The scheduler manages which jobs run where and when on an HPC system.

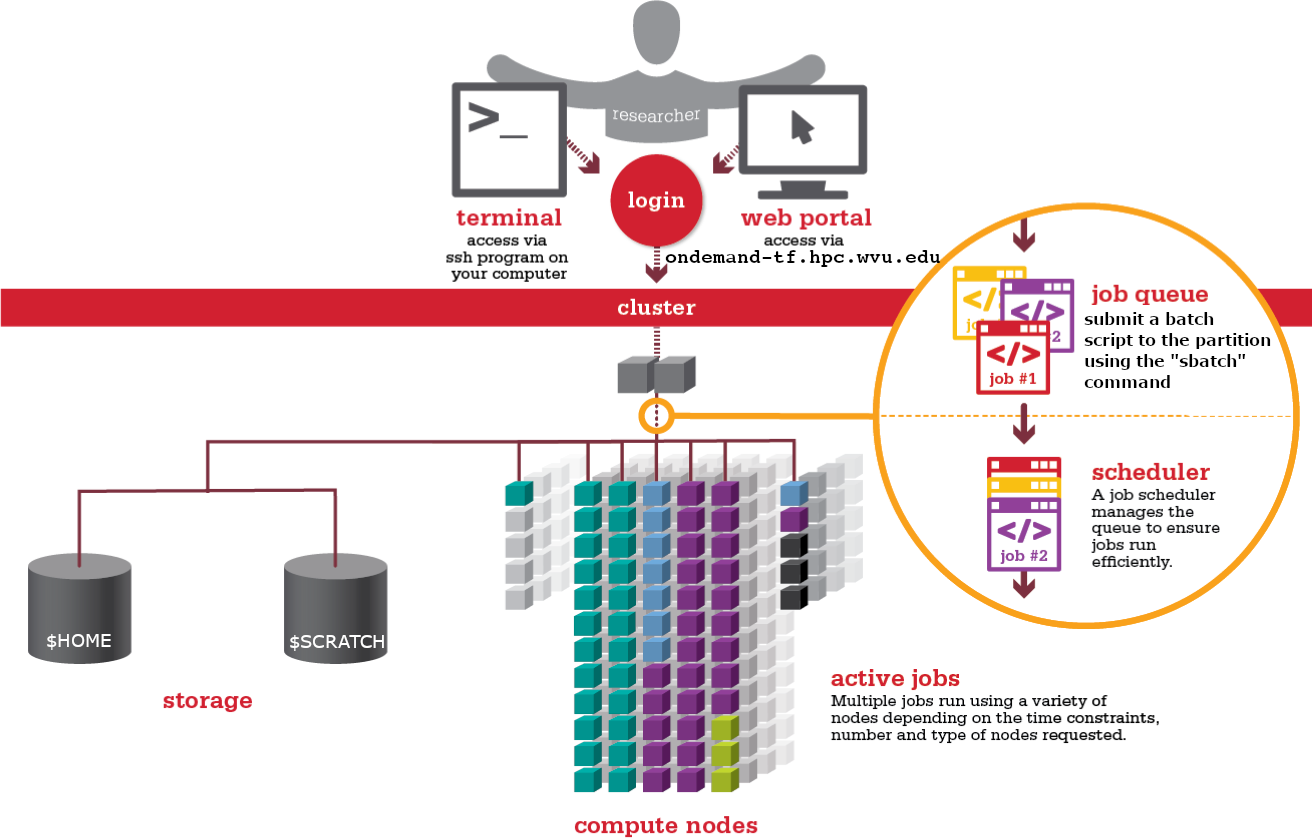
Why do supercomputers use queueing?

The scheduler used on our clusters is SLURM. SLURM is not the only resource manager or scheduler for HPC systems. Other software packages offer similar functionality. The exact syntax might change, but the concepts remain the same.

A Resource Manager takes care of receiving job submissions and executes those jobs when resources are available, providing the most efficient conditions for the jobs. On the other hand, a job scheduler is in charge of associating jobs with the appropriate resources and trying to maximize an objective function, such as total utilization constrained by priorities and the best balance between the resources requested and resources available. As SLURM is taking the dual role of Resource Manager and Scheduler, SLURM calls itself a Workload Manager, a term that better embraces the multiple roles taken by this software package.

Workload Manager on WVU Clusters

All of our clusters use SLURM today. On Thorny Flat, we have a compatibility layer so that most Torque/Moab batch scripts will still work. If you are new to WVU’s HPC clusters, it makes the most sense to learn the SLURM batch commands. See Slurm Quick Start Guide for more SLURM information.

What is a Batch Script?

The most basic use of the scheduler is to run a command non-interactively. This is also referred to as batch job submission. In this case, we need to make a script that incorporates some arguments for SLURM, such as the resources needed and the modules that need to be loaded.

We will use the sleep.sh job script as an example.

Parameters

Let’s discuss the example SLURM script, sleep.sh. Go to File Explorer and edit sleep.sh

$> cd $HOME
$> mkdir SLEEP
$> cd SLEEP
$> nano sleep.sh

Write the following in the file with your text editor:

#!/bin/bash

#SBATCH --partition=standby
#SBATCH --job-name=test_job
#SBATCH --time=00:03:00
#SBATCH --nodes=1 --ntasks-per-node=2

echo 'This script is running on:'
hostname
echo 'The date is :'
date
sleep 120

Comments in UNIX (denoted by #) are typically ignored. But there are exceptions. For instance, the special #! comment at the beginning of scripts specifies what program should be used to run it (typically /bin/bash). This is required in SLURM so don’t leave it out! Schedulers like SLURM also have a special comment used to denote special scheduler-specific options. Though these comments differ from scheduler to scheduler, SLURM’s special comment is #SBATCH. Anything following the #SBATCH comment is interpreted as an instruction to the scheduler.

In our example, we have set the following parameters:

Option	Name	Example Setting	Notes
`--partition`	queue	standby	See next section for queue info
`--job-name`	jobname	test_script	Name of your script (no spaces, alphanumeric only)
`--time`	total job time	multiple settings	See next segment
`--nodes`	nodes requested	multiple settings	See next segment
`--ntasks-per-node`	cores per node	multiple settings	See next segment

Resource list

A resource list will contain a number of settings that inform the scheduler what resources to allocate for your job and for how long (wall time).

Walltime

Walltime is represented by --time=00:03:00 in the format HH:MM:SS. This will be how long the job will run before timing out. If your job exceeds this time, the scheduler will terminate the job. You should find a usual runtime for the job and add some more (say 20%) to it. For example, if a job took approximately 10 hours, the wall time limit could be set to 12 hours, e.g. “–time=12:00:00”. By setting the wall time, the scheduler can perform job scheduling more efficiently and also reduces occasions where errors can leave the job stalled but still taking up resources for the default much longer wall time limit (for queue wall time defaults, run squeue command)

Walltime test exercise

Resource requests are typically binding. If you exceed them, your job will be killed. Let’s use wall time as an example. We will request 30 seconds of wall time, and attempt to run a job for two minutes.
#!/bin/bash

#SBATCH --partition=standby
#SBATCH --job-name=test_job
#SBATCH --time=00:00:30
#SBATCH --nodes=1 --ntasks-per-node=2

echo 'This script is running on:'
hostname
echo 'The date is :'
date
sleep 120
Submit the job and wait for it to finish. Once it has finished, check the error log file. In the error file, there will be
This script is running on:
This script is running on:
taicm002.hpc.wvu.edu
The date is :
Thu Jul 20 19:25:21 EDT 2023
slurmstepd: error: *** JOB 453582 ON taicm002 CANCELLED AT 2023-07-20T19:26:33 DUE TO TIME LIMIT ***
What happened?

Our job was killed for exceeding the amount of resources it requested. Although this appears harsh, this is a feature. Strict adherence to resource requests allows the scheduler to find the best possible place for your jobs. Even more importantly, it ensures that another user cannot use more resources than they’ve been given. If another user messes up and accidentally attempts to use all of the CPUs or memory on a node, SLURM will either restrain their job to the requested resources or kill the job outright. Other jobs on the node will be unaffected. This means that one user cannot mess up the experience of others, the only jobs affected by a mistake in scheduling will be their own.

Compute Resources and Parameters

Compute parameters The argument --nodes specifies the number of nodes (or chunks of resource) required; --ntasks-per-node indicates the number of CPUs per chunk required.

nodes	tasks	Description
2	16	32 Processor job, using 2 nodes and 16 processors per node
4	8	32 Processor job, using 4 nodes and 8 processors per node
8	28	244 Processor job, using 8 nodes and 28 processor per node
1	40	40 Processor job, using 1 nodes and 40 processors per node

Each of these parameters has a default setting they will revert to if not set; however, this means your script may act differently to what you expect.

You can find more information about these parameters by viewing the manual page for the sbatch function. This will also show you what the default settings are.

$> man sbatch

Setting up email notifications

Jobs on an HPC system might run for days or even weeks. We probably have better things to do than constantly check on the status of our job with squeue. Looking at the online documentation for sbatch (you can also google “sbatch slurm”), can you set up our test job to send you an email when it finishes?

Hint: you will need to use the --mail-user and --mail-type options.

Running a batch job (two methods)

Submit Jobs with job composer on OnDemand

OnDemand also has a tool for job creation and submission to the batch system. The same information as above applies since it still uses the same underlying queue system. In the Job Composer, you can create a new location in your home directory for a new job, create or transfer a job script and input files, edit everything, and submit your job all from this screen.

We will run this job in the Job Composer by creating a new job from specified path.

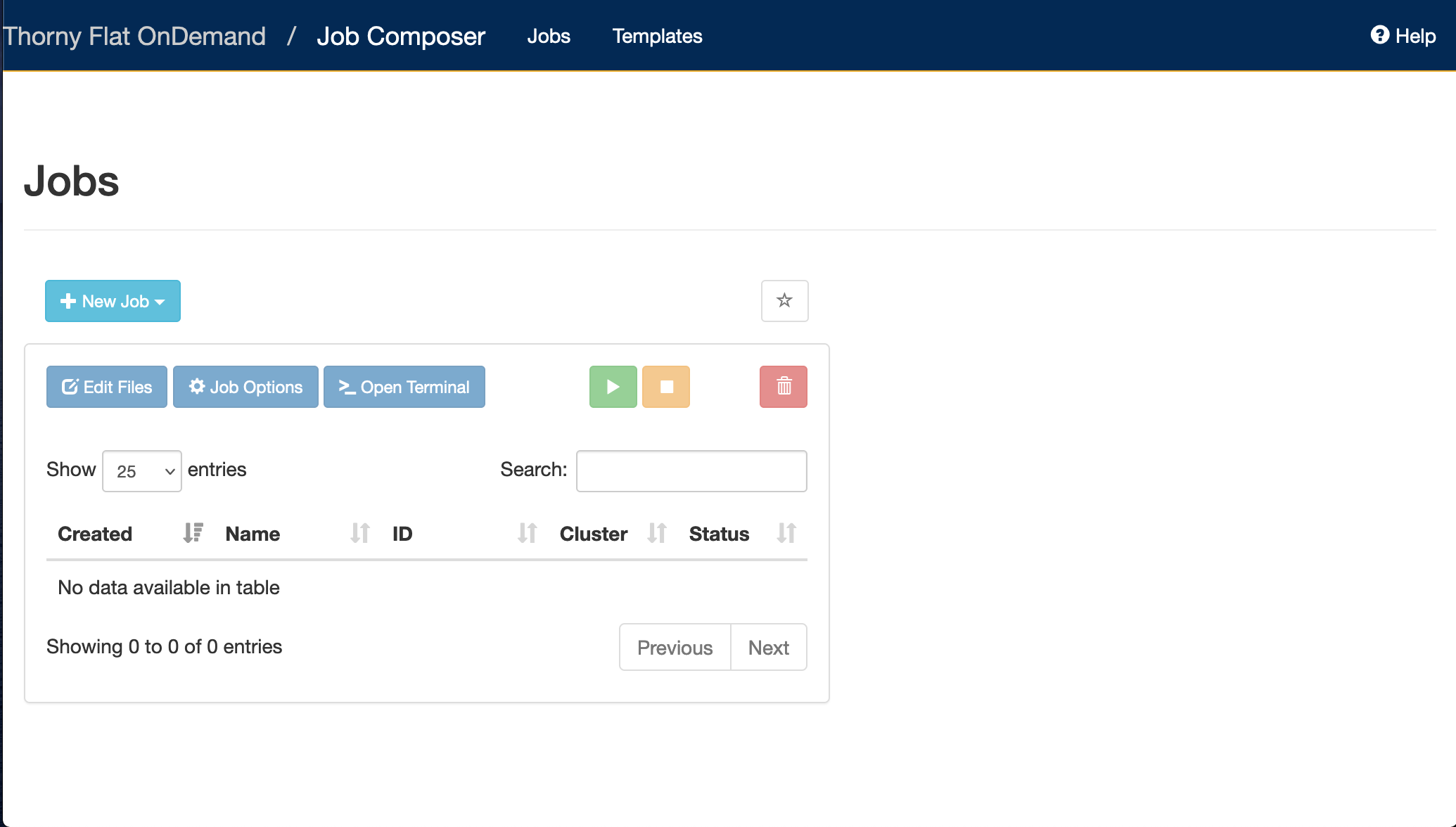
NewJob

You’ll see the Job Options page, like this:

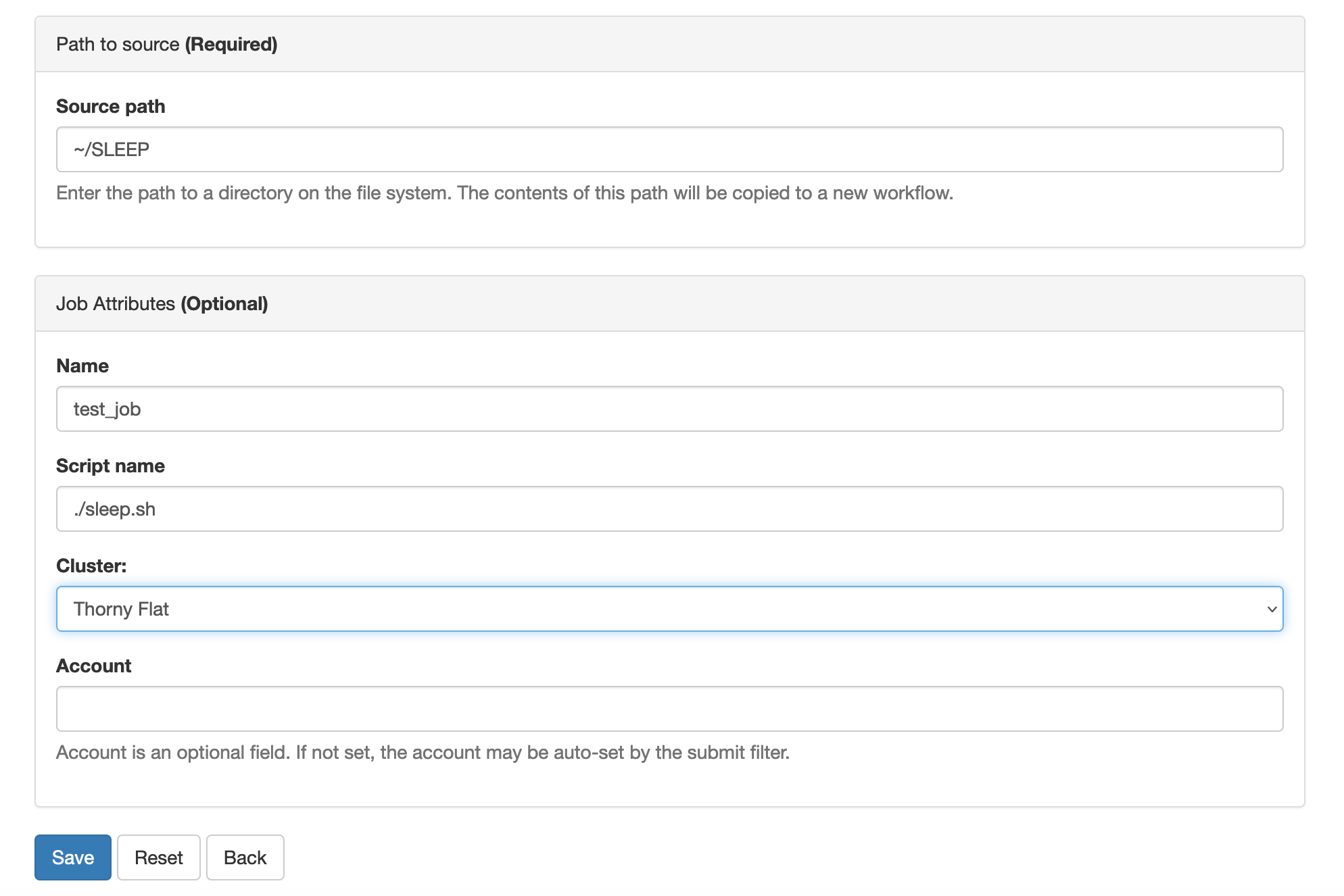
JobOptions

Fill it in as shown. Path is ~/SLEEP and then select Save.

To run the job, select green ‘play’ button.

If the job is successfully submitted, a green bar will appear on the top of the page.

Also, OnDemand allows you to view the queue for all systems (not just the one you are on in the shell) under Jobs, select Active Jobs. You can filter by your jobs, your group’s jobs, and all jobs.

Submitting Jobs via the command line

To submit this job to the scheduler, we use the sbatch command.

$> sbatch sleep.sh
Submitted batch job 453594
$>

The number that first appears is your Job ID. When the job is completed, you will get two files: an Output and an Error file (even if there is no errors). They will be named {JobName}.o{JobID} and {JobName}.e{JobID} respectively.

And that’s all we need to do to submit a job. To check on our job’s status, we use the command squeue.

$> squeue -u $USER
             JOBID PARTITION     NAME     USER ST       TIME  NODES NODELIST(REASON)
            453594   standby test_job gufranco  R       0:34      1 taicm009

We can see all the details of our job, most importantly if it is in the “R” or “RUNNING” state. Sometimes our jobs might need to wait in a queue (“PD”) or have an error. The best way to check our job’s status is with squeue. It is easiest to view just your own jobs in the queue with the squeue -u $USER. Otherwise, you get the entire queue.

Partitions (Also known as queues)

There are usually a number of available partitions (Other resource managers call them queues) to use on the HPC clusters. Each cluster has separate partitions. The same compute node can be associated with multiple partitions Your job will be routed to the appropriate compute node based on the list of nodes associated with the partition, the wall time, and the computational resources requested. To get the list of partitions on the cluster, execute:

$> sinfo -s
PARTITION       AVAIL  TIMELIMIT   NODES(A/I/O/T) NODELIST
standby*           up    4:00:00      94/71/2/167 taicm[001-009],tarcl100,tarcs[100,200-206,300-304],tbdcx001,tbmcs[001-011,100-103],tbpcm200,tbpcs001,tcbcx100,tcdcx100,tcgcx300,tcocm[100-104],tcocs[001-064,100],tcocx[001-003],tcscm300,tjscl100,tjscm001,tmmcm[100-108],tngcm200,tpmcm[001-006],tsacs001,tsdcl[001-002],tsscl[001-002],ttmcm[100-101],tzecl[100-107],tzecs[100-115]
comm_small_day     up 1-00:00:00        59/5/1/65 tcocs[001-064,100]
comm_small_week    up 7-00:00:00        59/5/1/65 tcocs[001-064,100]
comm_med_day       up 1-00:00:00          5/0/0/5 tcocm[100-104]
comm_med_week      up 7-00:00:00          5/0/0/5 tcocm[100-104]
comm_xl_week       up 7-00:00:00          3/0/0/3 tcocx[001-003]
comm_gpu_inter     up    4:00:00         8/1/2/11 tbegq[200-202],tbmgq[001,100],tcogq[001-006]
comm_gpu_week      up 7-00:00:00          5/0/1/6 tcogq[001-006]
aei0001            up   infinite          3/5/1/9 taicm[001-009]
alromero           up   infinite        12/2/0/14 tarcl100,tarcs[100,200-206,300-304]
be_gpu             up   infinite          1/1/1/3 tbegq[200-202]
bvpopp             up   infinite          0/1/0/1 tbpcs001
cedumitrescu       up   infinite          1/0/0/1 tcdcx100
cfb0001            up   infinite          0/1/0/1 tcbcx100
cgriffin           up   infinite          1/0/0/1 tcgcx300
chemdept           up   infinite          0/4/0/4 tbmcs[100-103]
chemdept-gpu       up   infinite          1/0/0/1 tbmgq100
cs00048            up   infinite          0/1/0/1 tcscm300
jaspeir            up   infinite          0/2/0/2 tjscl100,tjscm001
jbmertz            up   infinite        3/14/0/17 tbmcs[001-011,100-103],tbmgq[001,100]
mamclaughlin       up   infinite          1/8/0/9 tmmcm[100-108]
ngarapat           up   infinite          0/1/0/1 tngcm200
pmm0026            up   infinite          0/6/0/6 tpmcm[001-006]
sbs0016            up   infinite          0/2/0/2 tsscl[001-002]
spdifazio          up   infinite          0/2/0/2 tsdcl[001-002]
tdmusho            up   infinite          1/5/0/6 taicm[001-004],ttmcm[100-101]
vyakkerman         up   infinite          1/0/0/1 tsacs001
zbetienne          up   infinite        6/18/0/24 tzecl[100-107],tzecs[100-115]
zbetienne_large    up   infinite          6/2/0/8 tzecl[100-107]
zbetienne_small    up   infinite        0/16/0/16 tzecs[100-115]

Submitting resource requests

Submit a job that will use 1 node, 4 processors, and 5 minutes of walltime.

Job environment variables

SLURM sets multiple environment variables at submission time. The following variables are commonly used in command files:

Variable Name	Description
`$SLURM_JOB_ID`	Full jobid assigned to this job. Often used to uniquely name output files for this job, for example: srun - np 16 ./a.out >output.${SLURM_JOB_ID}
`$SLURM_JOB_NAME`	Name of the job. This can be set using the –job-name option in the SLURM script (or from the command line). The default job name is the name of the SLURM script.
`$SLURM_JOB_NUM_NODES`	Number of nodes allocated
`$SLURM_JOB_PARTITION`	Queue job was submitted to.
`$SLURM_NTASKS`	The number of processes requested
`$SLURM_SUBMIT_DIR`	The directory from which the batch job was submitted.
`$SLURM_ARRAY_TASK_ID`	Array ID numbers for jobs submitted with the -a flag.

Canceling a job

Sometimes we’ll make a mistake and need to cancel a job. This can be done with the qdel command. Let’s submit a job and then cancel it using its job number.

$> sbatch sleep.sh
Submitted batch job 453599

$> $ squeue -u $USER
             JOBID PARTITION     NAME     USER ST       TIME  NODES NODELIST(REASON)
            453599   standby test_job gufranco  R       0:47      1 tcocs015

Now cancel the job with it’s job number. Absence of any job info indicates that the job has been successfully canceled.

$> scancel 453599
$> squeue -u $USER
             JOBID PARTITION     NAME     USER ST       TIME  NODES NODELIST(REASON)

Detailed information about jobs

The information provided by the command squeue is sometimes not enough, and you would like to gather a complete picture of the state of a particular job. The command scontrol provides a wealth of information about jobs but also partitions and nodes. Information about a job:

$ sbatch sleep.sh
Submitted batch job 453604
$ scontrol show job 453604
JobId=453604 JobName=test_job
   UserId=gufranco(318130) GroupId=its-rc-thorny(1079001) MCS_label=N/A
   Priority=11588 Nice=0 Account=its-rc-admin QOS=normal
   JobState=RUNNING Reason=None Dependency=(null)
   Requeue=0 Restarts=0 BatchFlag=1 Reboot=0 ExitCode=0:0
   RunTime=00:00:19 TimeLimit=00:04:00 TimeMin=N/A
   SubmitTime=2023-07-20T20:39:15 EligibleTime=2023-07-20T20:39:15
   AccrueTime=2023-07-20T20:39:15
   StartTime=2023-07-20T20:39:15 EndTime=2023-07-20T20:43:15 Deadline=N/A
   PreemptEligibleTime=2023-07-20T20:39:15 PreemptTime=None
   SuspendTime=None SecsPreSuspend=0 LastSchedEval=2023-07-20T20:39:15 Scheduler=Main
   Partition=standby AllocNode:Sid=trcis001:31864
   ReqNodeList=(null) ExcNodeList=(null)
   NodeList=taicm007
   BatchHost=taicm007
   NumNodes=1 NumCPUs=2 NumTasks=2 CPUs/Task=1 ReqB:S:C:T=0:0:*:*
   TRES=cpu=2,node=1,billing=2
   Socks/Node=* NtasksPerN:B:S:C=2:0:*:* CoreSpec=*
   MinCPUsNode=2 MinMemoryNode=0 MinTmpDiskNode=0
   Features=(null) DelayBoot=00:00:00
   OverSubscribe=OK Contiguous=0 Licenses=(null) Network=(null)
   Command=/gpfs20/users/gufranco/SLEEP/sleep.sh
   WorkDir=/gpfs20/users/gufranco/SLEEP
   StdErr=/gpfs20/users/gufranco/SLEEP/slurm-453604.out
   StdIn=/dev/null
   StdOut=/gpfs20/users/gufranco/SLEEP/slurm-453604.out
   Power=

Interactive jobs

Sometimes, you will need a lot of resources for interactive use. Perhaps it’s the first time running an analysis, or we are attempting to debug something that went wrong with a previous job.

You can also request interactive jobs on OnDemand using the Interactive Apps menu.

To submit an interactive job requesting 4 cores on the partition standby and with a wall time of 40 minutes, execute:

$> srun -p standby -t 40:00 -c 4 --pty bash

Another example includes requesting a GPU compute compute, execute:

$> srun -p comm_gpu_inter -G 1 -t 2:00:00 -c 8 --pty bash

Job arrays

Job arrays offer a mechanism for submitting and managing collections of similar jobs quickly and easily; job arrays with many tasks can be submitted from a single submission script. Job arrays are very useful for testing jobs when one parameter is changed or to execute the same workflow on a set of samples.

For our example, we will create a folder FIBONACCI and a submission script called fibo.sh

$> mkdir FIBONACCI
$> cd FIBONACCI/
$> nano fibo.sh

Write the content of the submission script as follows:

#!/bin/bash

#SBATCH --partition=standby
#SBATCH --job-name=test_job
#SBATCH --time=00:03:30
#SBATCH --nodes=1 --ntasks-per-node=2
#SBATCH --array 1-10

# Static input for N
N=10

# First Number of the
# Fibonacci Series
a=$SLURM_ARRAY_TASK_ID

# Second Number of the
# Fibonacci Series
b=`expr $SLURM_ARRAY_TASK_ID + 1`

echo "10 first elements in the Fibonacci Sequence."
echo ""
echo "Starting with $a and $b"
echo ""

for (( i=0; i<N; i++ ))
do
    echo -n "$a "
    fn=$((a + b))
    a=$b
    b=$fn
done
# End of for loop
echo ""
sleep 60

The array index values on job arrays are specified using the --array or -a option of the sbatch command. All the jobs in the job array will have the same variables except for the environment variable SLURM_ARRAY_TASK_ID , which is set to its array index value. This variable can redirect the workflow to a different folder or execute the simulation with different parameters.

Submit the job array:

$> sbatch fibo.sh
Submitted batch job 453632
$> squeue -u $USER
         JOBID PARTITION     NAME     USER ST       TIME  NODES NODELIST(REASON)
      453632_1   standby test_job gufranco  R       0:03      1 taicm007
      453632_2   standby test_job gufranco  R       0:03      1 taicm007
      453632_3   standby test_job gufranco  R       0:03      1 taicm007
      453632_4   standby test_job gufranco  R       0:03      1 taicm007
      453632_5   standby test_job gufranco  R       0:03      1 taicm007
      453632_6   standby test_job gufranco  R       0:03      1 taicm007
      453632_7   standby test_job gufranco  R       0:03      1 taicm007
      453632_8   standby test_job gufranco  R       0:03      1 taicm007
      453632_9   standby test_job gufranco  R       0:03      1 taicm007
     453632_10   standby test_job gufranco  R       0:03      1 taicm007

The job submission will create ten jobs When the jobs finish, their output will be in files slurm-XXX. For example:

$> cat slurm-453632_7.out
10 first elements in the Fibonacci Sequence

Starting with 7 and 8

7 8 15 23 38 61 99 160 259 419

Key Points

The scheduler handles how compute resources are shared between users.

Everything you do should be run through the scheduler.

A non-interactive job is expressed as a shell script that is submitted to the cluster.

Try to adjust the wall time to around 10-20% more than the expected time the job should need.

It is a good idea to keep aliases to common torque commands for easy execution.

Terminal Multiplexing: tmux

Overview

Teaching: 60 min
Exercises: 30 min

Topics

What is a Terminal Multiplexer?

How can I use tmux?

Objectives

Learn about Sessions, Windows and Panes

Terminal Emulation

During your interaction with an HPC cluster, you spend most of your time in front of a terminal. We have been working on a terminal during the previous two episodes. Let’s understand what a terminal is before digging into terminal multiplexing and tmux in particular.

What you have on your computer is called a terminal emulator. In the old days of mainframes (70s and 80s), people using computers worked on what were called dumb terminals, monitors with keyboards but no processing power, all the processing was happening on a remote machine, the mainframe.

Today, what you have on your side is a perfectly capable computer, but you are using a terminal emulator and an SSH client to connect to a remote machine that is the head node of the cluster. On Windows, you have applications like PuTTy https://www.chiark.greenend.org.uk/~sgtatham/putty/ that will offer an xterm terminal emulator and the SSH client on the same package. You should realize that the terminal emulator and SSH client are two different applications. In other Operating Systems like Linux and MacOS the difference between the terminal emulator and the SSH client is more clear.

Now, on your computer, connect to one of our HPC clusters using SSH. You notice that your prompt, the string that indicates that it is ready to receive commands, shows the name of the head node on our clusters. Imagine that you are editing a text file using any of the three editors from our previous episode. If, for some reason, the internet connection fails, the program that you were using will be closed. Some editors give you some recovery protection, but in any case, you need to connect again, change the working directory and other operations before opening the file, and continue your work.

Another limitation of traditional terminals is that you have just one place to enter commands. Working with HPC clusters usually involves working with several jobs and projects, and you would like to write and submit new jobs, check the status of those jobs that you have already submitted, and read the output from the jobs that have been finished. You could open more SSH sessions, but the chances of those sessions failing due to network issues and managing those extra windows limit your ability to work effectively on the cluster.

The solution for the two problems above is using a Terminal Multiplexer, a program that runs on the head node and is detached from your local terminal session. tmux is such a terminal multiplexer that it can create multiple emulated terminals.

In this episode we will show you how to create tmux sessions on the cluster and see the effect of detaching and reattaching to the session. Next, we will see the four basic concepts in tmux: Clients, Sessions, Windows and Panes. We will see how to create and move between them and, finally, a few tricks on how to personalize your experience on tmux. As you progress on the use of the cluster tmux will become an important companion for your interaction with the HPC clusters.

tmux lets you switch easily between several virtual terminals organized in sessions, windows, and panes. One big advantage of terminal multiplexing is that all those virtual terminals remain alive when you log out of the system. You can work remotely for a while, close the connection and reconnect, attach your tmux session, and continue exactly where you left your work.

Opening a tmux Session and Client

The first concepts in tmux are client and session. A tmux session is made of at least one window that holds at least one pane. We will see about windows and panes later in this episode but right now, lets see how to work with tmux sessions.

First, connect to the cluster using your terminal emulator and SSH client. Once you are connected to the head node of the cluster, execute:

tmux

If, for some reason, you lost the connection to the server or you detached from the multiplexer, all that you have to do to reconnect is to execute the command:

tmux a

You will see something new here: a green bar on the bottom of your screen. That is the indication that you are inside a tmux session. The tmux status line at the bottom of the screen shows information on the current session. At this point, you have created one tmux client that is attached to the session that was also created. Clients and Sessions are separate entities, allowing you to detach your client from the session and reattach it later. You can also have several clients attached to the same session, and whatever you do on one will be visible on the others. At first sessions and client could be confused, but this exercise will help you understand the concepts.

You are now on a tmux session. Open nano so you can see the top bar and the two command bars on the bottom from the nano session. Write a line like you were writing a text file. All commands inside a session use a prefix key combination. The prefix combination is Ctrl+B, also referred as C-b. You have to press the Ctrl key, keep it pressed and press the B key followed for any command for tmux to interpret. The first command will detach a session from the client. Use the combination C-b d to detach the current session from the client. You will hit the Ctrl key, keep it pressed, and press B, raise both keys, and press D. You will see that the nano top and bottom bars disappear, the green tmux bottom bar also disappears, and you return to your normal terminal. You can go even further and close your terminal on your computer to simulate a loss in internet connection. Reconnect again to the cluster using SSH to return to the head node.

From the head node, we will reattach the session using:

$ tmux a

You will see your session recovering exactly the same as you left when you detached, and nano should be there with the line that you wrote. You have created your first tmux session and that session will persist until you kill the session or the head node is rebooted, something that happens rarely, usually one or two times per year. For the most part, you can keep your tmux session open

You can create several tmux sessions, each one with a given name, using:

$ tmux new -s <session_name>

Having several sessions is useful if you want a distinctive collection of windows for different projects, as they are more isolated than windows on the same session. Changing between sessions is done with C-b ( and C-b ) to move between the previous and next session. Another way of moving between sessions is using C-b w as we will see next, showing all the windows across all sessions and allowing you to jump into windows from different sessions.

Sessions have names, and those names can be changed with C-b $

Windows and Panes

The next concepts on tmux are windows and panes. A tmux window is the area that fills the entire space offered by your local terminal emulator. Windows has the same purpose as tabs on a browser. When you create your first tmux session, you also create a single window. tmux windows can be further divided in what tmux calls panes. You can divide a single tmux window in multiple panes and you can have several tmux windows on a single tmux session. As we will see in a moment, you can have several tmux sessions attached to tmux clients or detached from them. Each session can hold several tmux windows and each window will have one or more tmux panes. On each of those panes, you will have a shell waiting for your commands. At the end tmux is the equivalent of a window manager in the world of terminals, with the ability to attach and detach at will and running commands concurrently.

In case you are not already attached to the tmux session, enter into the tmux session with:

$ tmux a

You have one window with one pane inside that fills the entire space. You can create new tmux windows with C-b c. Start creating a few of them. Each new window will appear in the bottom tmux bar. The first ten are identified with a number from a digit number from 0 to 9.

Moving between windows is done using the number associated on the bottom bar of tmux, to move to the first window (with number 0) use C-b 0, similarly for all the first 10 windows. You can create more windows beyond the first 10, but only for those you can jump into them using the **C-b ** combination. Another way of moving between the previous and next window. Use **C-b p** and **C-b n** for the previous and next respectively. You can change the number of a window using **C-b .**

Notice that windows receive names shown on the bottom bar in tmux. You can change the name of the window using C-b ,. This is useful for generating windows with consistent names for tasks or projects related to the window. You can also use the different windows connected to different machines so the label could be useful to identify which machine you are connected to at a given window.

You can kill the current window with C-b & and see all the windows across all sessions with C-b w. This is another way of moving between windows in different sessions.

The last division in the hierarchy is panes. Panes create new terminals by dividing the window horizontally or vertically. You can create new panes using C-b % for vertical division or C-b “ for horizontal division.

You can move between panes with C-b o or use the arrows to go to the panes in the direction of the arrow, such as **C-b **

One easy way of organizing the panes is using the predefined layouts, and C-b SPACE will cycle between them. Panes can be swapped with C-b { and C-b }. You can zoom into the current pane to take the whole window using C-b z and execute the same command to return to the previous layout.

Copy mode

All the commands above are related to the movement and creation of sessions, windows, and panes. Inside a pane, you can enter Copy mode if you want to scroll the lines on the pane or copy and paste lines. The procedure to use copy mode is as follows:

Press C-b [ to enter in copy mode.
Move the start/end of text to highlight.
Press C-SPACEBAR to start selection

Start highlighting text. Selected text changes the color and background, so you'll know if the command worked.

Move to the opposite end of the text to copy.
Press ALT-w to copy selected text into tmux clipboard.
Move cursor to opposite tmux pane, or completely different tmux window. Put the cursor where you want to paste the text you just copied.
Press C-b ] to paste copied text from tmux clipboard.

If you work from a Mac, the ALT key (In macOS called option) will not work. One alternative is to use vi-copy mode:

Press C-b : and write: setw -g mode-keys vi
Now enter in copy mode with C-b [
To start selecting the text, use SPACEBAR
Move to the opposite end of the text to copy
Copy the selection with ENTER
Go to the window and pane you want to paste
Press C-b ] to paste copied text from tmux clipboard.

Final remarks

tmux is far more than the few commands shown here. There are many ways to personalize the environment. Some personalizations involve editing the file $HOME/.tmux.conf

Consider for example, this .tmux.conf that changes several colors in the tmux status bar.

######################
### DESIGN CHANGES ###
######################

# loud or quiet?
set -g visual-activity off
set -g visual-bell off
set -g visual-silence off
setw -g monitor-activity off
set -g bell-action none

#  modes
setw -g clock-mode-colour colour5
setw -g mode-style 'fg=colour1 bg=colour18 bold'

# panes
set -g pane-border-style 'fg=colour19 bg=colour0'
set -g pane-active-border-style 'bg=colour0 fg=colour9'

# statusbar
set -g status-position bottom
set -g status-justify left
set -g status-style 'bg=colour18 fg=colour137 dim'
set -g status-left ''
set -g status-right '#[fg=colour233,bg=colour19] %d/%m #[fg=colour233,bg=colour8] %H:%M:%S '
set -g status-right-length 50
set -g status-left-length 20

setw -g window-status-current-style 'fg=colour1 bg=colour19 bold'
setw -g window-status-current-format ' #I#[fg=colour249]:#[fg=colour255]#W#[fg=colour249]#F '

setw -g window-status-style 'fg=colour9 bg=colour18'
setw -g window-status-format ' #I#[fg=colour237]:#[fg=colour250]#W#[fg=colour244]#F '

setw -g window-status-bell-style 'fg=colour255 bg=colour1 bold'

# messages
set -g message-style 'fg=colour232 bg=colour16 bold'

There are a lot of things that can be changed to everyone’s taste. There are several .tmux.conf files shared on GitHub and other repositories that customize tmux in several ways.

Exercise: TMUX Sessions, Windows and Panes

This exercise will help you familiarize yourself with the three concepts in TMUX.

Create three sessions on TMUX, and give each of them different names, either creating the session with the name or using C-b $ to rename session names.

In one of those sessions, create two windows, and in the other, create three windows. Move between sessions to accomplish this.

In one of those windows, split the window vertically, on another horizontally, and on the third one create 3 panes and cycle between the different layouts using C-b SPACE

Detach or close your terminal and reconnect, attach your sessions, and verify that your windows and panes remain the same.

Exercise: Using tmux

Using the tables above, follow this simple challenge with tmux

Log in to Thorny Flat and create a tmux session

Inside the session, create a new window

Go back to window 0 and create a horizontal pane, and inside one of those panes, create a vertical pane.

Create a big clock pane

Detach from your current session, close your terminal, and reconnect. Log in again on Thorny Flat and reattach your session.

Now that you are again in your original session create a new session. You will be automatically redirected there. Leave your session and check the list of sessions.

Kill the second session (session ID is 1)

Reference of tmux commands

In tmux, by default, the prefix is Ctrl+b. Use the prefix followed by one of the options below:

Sessions

    :new<CR>  new session
    s  list sessions
    $  name session

Windows (tabs)

    c  create window
    w  list windows
    n  next window
    p  previous window
    f  find window
    ,  name window
    &  kill window

Panes (splits)

    %  vertical split
    "  horizontal split
    o  swap panes
    q  show pane numbers
    x  kill pane
    +  break pane into window (e.g. to select text by mouse to copy)
    -  restore pane from window
    ⍽  space - toggle between layouts
    q (Show pane numbers, when the numbers show up type the key to goto that pane)
    { (Move the current pane left)
    } (Move the current pane right)
    z toggle pane zoom

Copy model

    [  Copy mode

In copy mode, use these commands to copy a region to the tmux clipboard.

    Ctrl SPACE  Start Selection
    Alt w       Copy the selection to the clipboard

After this use the command to paste

    ]  Paste from clipboard

Others

    d  detach
    t  big clock
    ?  list shortcuts
    :  prompt

Command line arguments for tmux

    tmux ls                       list sessions
    tmux new                      new session
    tmux rename -t <ID> new_name  rename a session
    tmux kill-session -t <ID>     kill session by target

Key Points

tmux allows you to keep terminal sessions on the cluster that persist in case of network disconnection.

Adjurn

Overview

Teaching: min
Exercises: min

Topics

Objectives

Key Points

Computational Partial Differential Equations

Overview

Teaching: 90 min
Exercises: 30 min

Topics

What is are differential equations and why are computers used to solve them?

How can I use the HPC cluster to solve PDEs for several scientific use cases?

Objectives

Learn about PDEs in the context of Computational Fluid Dynamics and Relativity

Computational Partial Differential Equations

Irene S. Nelson, PhD

Day 1: Background and Fluid Dynamics

Introduction: Partial Differential Equations

In research, when considering some quantity, we often find that how that quantity changes is just as, if not more interesting than the value. To that end, we often find ourselves looking at the instantaneous rate of change in a variable (called the derivative, found through a process called differentiation) alongside the value of that variable itself. An example of this concept that can often be seen in day-to-day life is the odometer and spedometer in your car. The car’s odometer measures the total distance that the car has travelled, but moment-to-moment, it’s much more important the car’s speed as shown by the spedometer. By definition, speed is the first derivative of distance. We can also differentiate speed again to find the second derivative, our car’s acceleration.

Another common way to think of the derivative is as the slope of a curve at a point. We illustrate this below with a simple parabola shown with its tangent line at the point $x=1$

import numpy as np
import matplotlib.pyplot as plt

x            = np.linspace(-5,5,20)
y            = x*x
tangent_line = 2*x-1

plt.figure()
plt.plot(x,y)
plt.plot(x,tangent_line)
plt.show()

png

As such, a differential equation is just any equation that involves a variable and the derivatives of that variable. These equations have numerous and important applications in diverse fields ranging from finance (compound interest) to ecology (population growth) and physics.

In physics, differential equations pop up in everything from quantum mechanics and thermodynamics to electromagnetism and general relativity. In these sessions, we will be focusing on three particular sets of equations:

The Navier-Stokes equations of thermodynamics
Maxwell’s equations of electromagnetism
Einstein’s equations of general relativity

As powerful as these equations are, they are also very complicated. It has been proven that general solutions to these equations simply do not exist, and the only exact solutions to these equations are limited to only the most simple cases that are extremely unlikely to occur in reality. For example, an exact solution to the equations of thermodynamics might be a completely sealed, completely still volume of air with constant temperature and pressure through the container. While these exact solutions do have their applications, most systems of interest are much, much more complicated. If you want to model a thermodynamic system such as Earth’s atmosphere to predict weather, we must find approximate solutions.

Approximate Solutions

The variables in a differential equation take on numbers that are continuous. When we way that a variable is continuous, we mean that for any two points in time, no matter how close they are, there are more points in between them. However, a computer cannot work that way. A computer would need to be infinitely large in order to record the pressure at each of infinitely many points in space. This applies to time as well. As such, we will need to quantize our domain, that is, break it down into small pieces, as if they were building blocks.

To do this in space, we will subdivide our domain of interest into a grid of cells. In each of these cells, we will sample each of the quantities we care about (this often includes derivatives as well). That is, we will consider the value of a variable throughout a grid cell to be the what we measure at a single point (typically the center) of that cell. We will do a similar process in time as well, only considering the value of these quantities at discrete points in time, which we call timesteps.

So, approximating a differential equation will involve taking a starting value for the variable of interest and estimating the change in that variable over the course of one timestep. This must then be done for every grid cell in domain. Consider compound interest, for example. The balance of a bank account at the beginning of the next month will be equal the balance at the beginning of the current month, plus interest. While we can solve this simple equation exactly for continuously compounding interest, banks will instead calculate it monthly. That is, once a month, they will take the balance, multiply it by the interest rate, and then add that much money to the balance.

With these approximations made, we are ready to begin simulating our system of choice. We can sort the differential equations that govern our system into two categories: constraint equations and evolution equations. Constraint equations tell us how our variables should behave at a single point in time; they can be used to generate initial data and to help verify that our approximations at later times are close to reality. Evolution equations then tell us how these quantities change over time.

We must also consider the boundaries of our computational domain. Our domain must necessarily be finite in size, but it will be influenced by the world outside of it. We model this using boundary conditions. For example, if we wanted to model air flow through a duct, a boundary condition might mimic the solid sides of the duct, as well as the inflow and outflow. If not done properly, this can result in weird, unphysical results, like gravitational waves reflecting inwards off the boundary of our domain.

Thus, the scheme to approximate a differential equation looks like this:

Setup initial data.
- Calculate the initial value of a variable at some predetermined point within each grid cell using the constraint equations.
Advance forward in time. For each timestep:

A. Estimate how much the variable should change over the course of the timestep within each grid cell using the evolution equations. Add this value to the variable for the next timestep.

B. Apply boundary conditions near the edge of the domain.

Example: Laminar flow through a pipe

Start an interactive job through OnDemand

from IPython.display import Image
from IPython.core.display import HTML 
Path = "screenshots/ansys/"

Image(Path + "0_Interactive_Job.png")

png

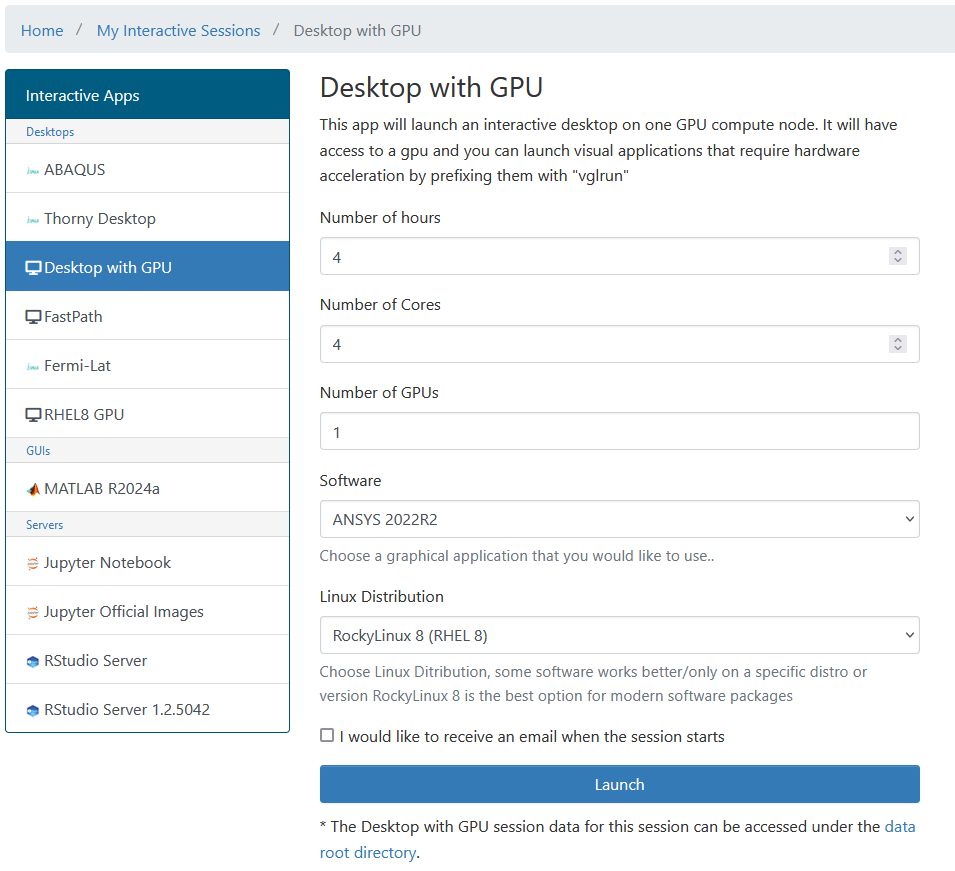
Image(Path + "1_Blank_Project.png")

png

To create a new project with Fluent, drag it to the workspace. Start DesignModeler by double-clicking on “Geometry”

Image(Path + "1a_New_Project.png")

png

Image(Path + "2_Design_Modeler.png")

png

Select the XY Plane.

Go to the sketching tab and draw a circle. Under dimensions, add a diameter and set this to 0.2m.

Image(Path + "2b_Circle.png")

png

Select the Extrude tool. Set the depth to 3.0m.

Image(Path + "2b_Extrude_Cylinder.png")

png

Double-click on “Mesh” to open the meshing software.

Right-clicking on Mesh, add a method. Selecting our pipe, click apply and set the method to Tetrahedrons.

Image(Path + "3_Meshing_Method.png")

png

Click Generate, the change to the Selection tab and select “Faces”.

Image(Path + "3b_Meshing_Done.png")

png

Select the ends of the pipe and name them “Inlet” and “Outlet”. Do the same for the “Wall” of the pipe.

Image(Path + "3c_Name_Selections.png")

png

After closing out of the meshing program, right-click on meshing and click “update”.

Double-click on Setup. Make sure Double Precision is selected and set the number of solver processes to the number of cores we want to use (in our case, 4).

Under model, change the Viscous model to Laminar.

Image(Path + "4_Model.png")

png

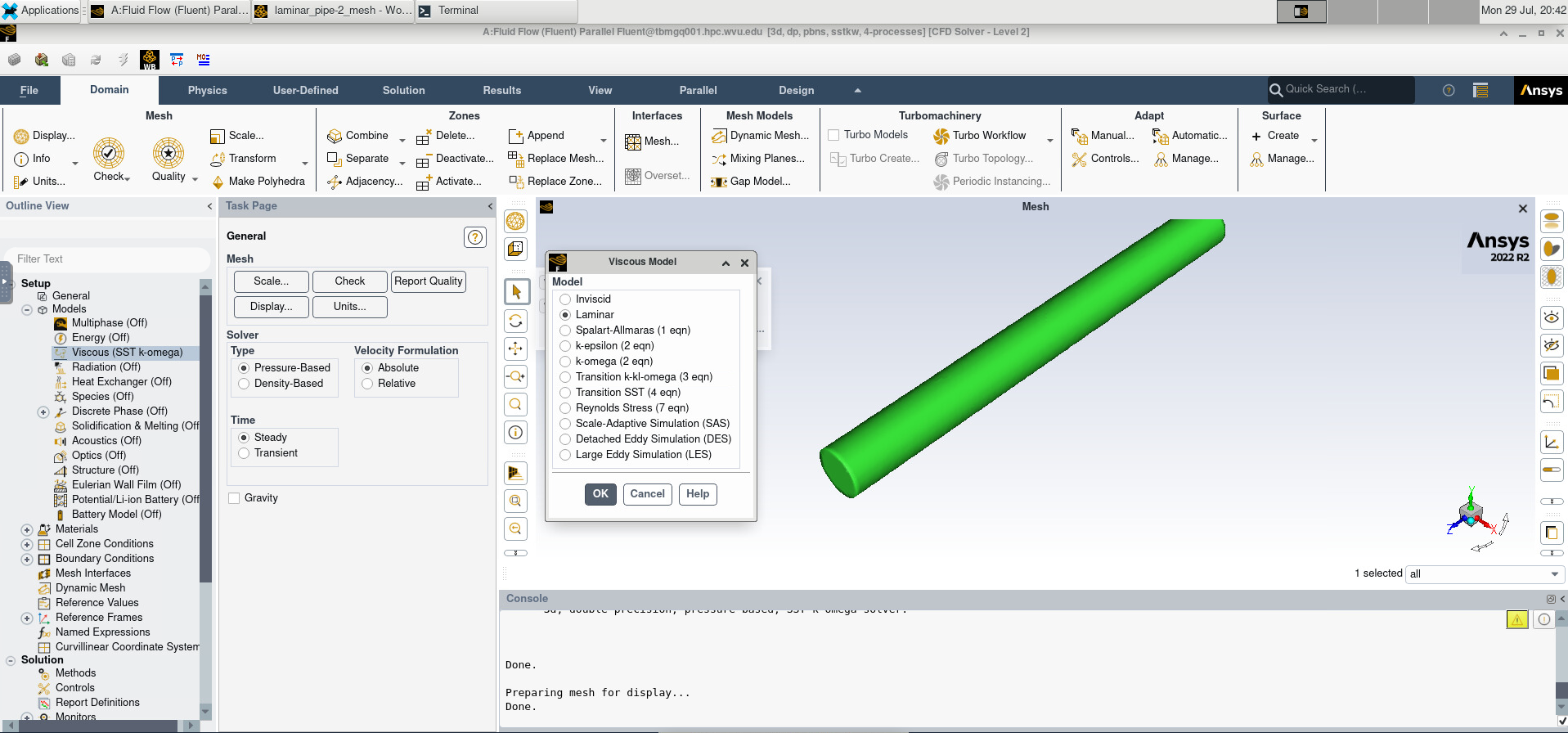
Under Materials > Fluid, select air. Change the density to 1 kg/m$^3$ and the viscosity to 0.002 kg/(ms). Make sure to click change/create before closing the window.

Under Boundary Conditions, change the inlet boundary condition to 1.0 m/s and the outlet boundary condition to 1 atm (101325 Pa).

Image(Path + "4a_Boundary_Conditions.png")

png

Under Initialization, we will use Standard Initialization and compute from the inlet.

Image(Path + "4b_Initialize.png")

png

Then, we click “Run Calculation”. After setting the Number of Iterations to 200, we click “Calculate”

Image(Path + "4c_Calculate.png")

png

Open the Results window. Click “Location” and select the the XZ-plane.

Image(Path + "6_Plane.png")

png

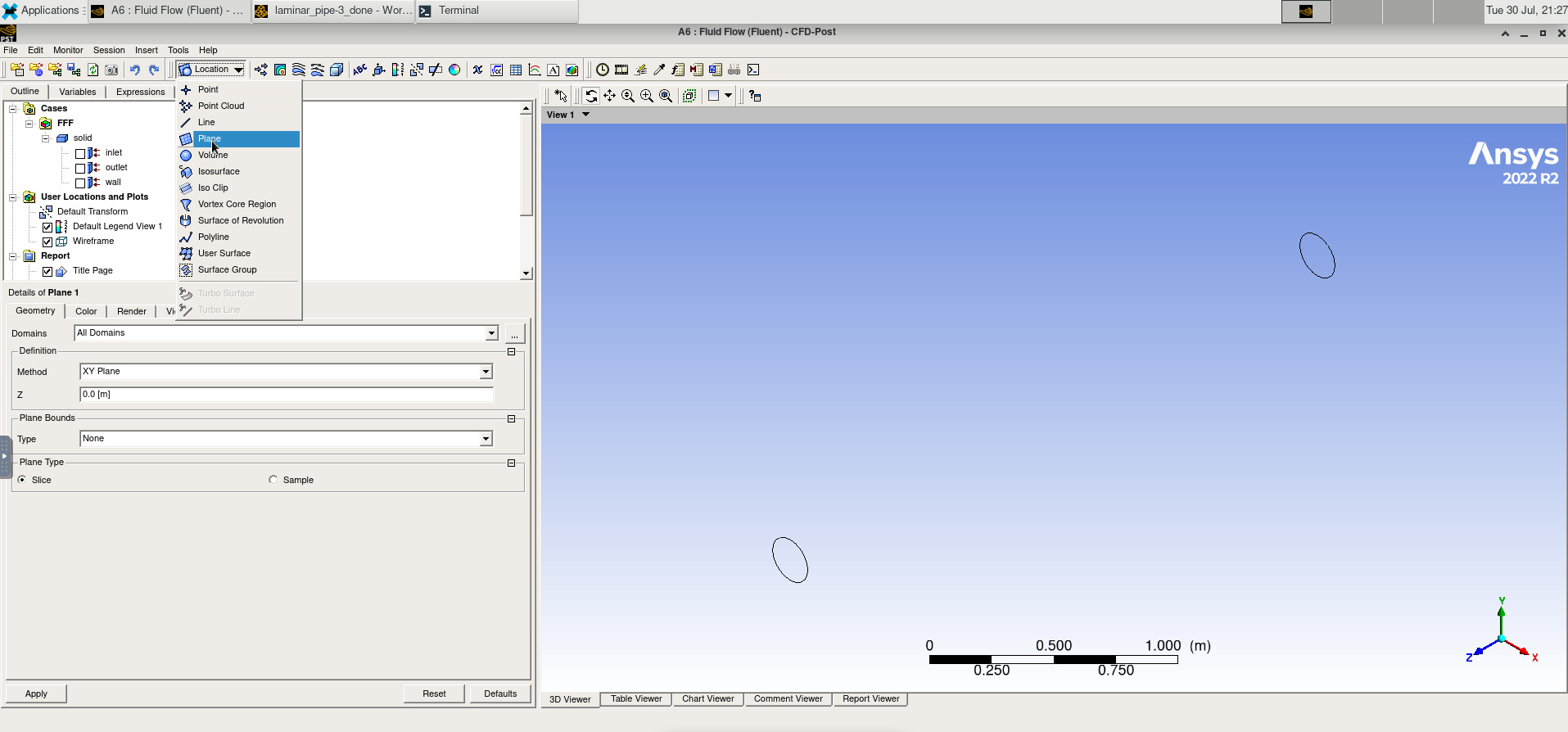
Then add a contour and select the location we just created and set the variable to velocity.

Image(Path + "6a_Contour.png")

png

Example: Flow over a Cylinder

A note on Grid sizing

It is very important that we select an appropriate size grid for our simulation. We must make sure that we adequately sample the space in order to resolve any interesting features in the physical system we are trying to simulate. This is because that when we try to numerically estimate derivatives on a grid, we essentially are trying to “guess” the actual shape of the underlying function from surrounding points. If we do not sample finely enough, we risk coming up with answers that do not match reality.

We can see this in the example below: when we undersample, there are many different functions that could fit the points, and they do not agree as to what the slope of the curve should be at our sampling points.

x = np.linspace(-np.pi/2,np.pi/2,2)
y = np.sin(x)

x1 = np.linspace(-3,3,50)
y1 = x1*2/np.pi
y2 = -1.167 + 0.636*x1 + 0.473*x1*x1

plt.figure()
plt.plot(x,y,'o')
plt.plot(x1,y1)
plt.plot(x1,y2)
plt.axis([-3.0, 3.0, -2.0, 2.0])
plt.show()

png

plt.figure()
x = np.linspace(-3*np.pi/4,3*np.pi/4,7)
plt.plot(x,np.sin(x),'o')

plt.plot(x1,np.sin(x1))
plt.show()

png

However, finer sampling comes at the cost of rapidly increasing how much memory and time your simulation you will require.

After creating a new project, we will open its properties and set the analysis type to 3D.

Image(Path + "7_Project_Properties.png")

png

Then we create a 15-by-32 meter rectangle and a 1 m diameter circle. These represent our computational domain and the cylinder.

Image(Path + "8_Grid_On.png")

png

Image(Path + "8a_Rectangle.png")

png

Image(Path + "8b_Rectangle.png")

png

In the toolbar, select Concept > Surface from Sketches. Select Sketch1 and click apply, then click Generate. Selecting the Created Surface Body, we set it to Fluid.

In Geometry, set the thickness to 0 m because we are working with a 2D problem.

Image(Path + "9_Thickness.png")

png

We will once again add a method, this time setting it to triangles, and the sizing to 0.3 m.

Image(Path + "9b_Method.png")

png

We will also add Sizing, setting it to the edge of the cylinder and setting the spacing to 0.025 m

Image(Path + "9c_Edge_Sizing.png")

png

We will also add Inflation, applying it to the fluid domain. Set the Boundary to the edge of the cylinder. Using the First Layer Thickness method, we set the first layer height to 0.025 m. We will also set the layers to 40 and the growth rate to 2.5

We will once again create named selections, naming the inlet, outlet, walls, and cylinder in our setup.

Change from a Steady to Transient solver. Again, we change the model to laminar flow. We will also set the density and viscosity to 1.

The only thing we will change with the boundary conditions is to set the inlet velocity to 80.

In Reference Values, we will calculate from the inlet.

Under Solution Methods, we set the Transient Formulation to Second Order Implicit.

Next we initialize using hybrid initialization.

In Calculation Activities, we tell the simulation to save every fifth frame.

Finally, we will run the calculation with a step size of 0.01, 20 iterations per time step, and 50 iterations.

We will create a plot for the surface body at symmetry 1, plotting the velocity.

Using the time step selector, we can also view what the system looked like at earlier times.

Image(Path + "9d_Contour.png")

png

Key Points

Examples of codes solving PDEs are Fluent and the Einstein Toolkit

Adjurn

Overview

Teaching: min
Exercises: min

Topics

Objectives

Key Points

Introduction to Machine Learning

Overview

Teaching: 60 min
Exercises: 30 min

Topics

What is Machine Learning?

How I can use tmux?

Objectives

Learn about Sessions, Windows and Panes

Machine Learning for Scientists in a hurry

Boilerplate

!if [ ! -f helpers.py ]; then wget "https://raw.githubusercontent.com/romerogroup/Notebooks_4SIAH/main/Machine_Learning/helpers.py"; fi

# import some custom helper code
import helpers
from helpers import set_css_in_cell_output
get_ipython().events.register('pre_run_cell', set_css_in_cell_output)

!pip install watermark

Defaulting to user installation because normal site-packages is not writeable
Requirement already satisfied: watermark in /Users/guilleaf/Library/Python/3.11/lib/python/site-packages (2.4.3)
Requirement already satisfied: ipython>=6.0 in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from watermark) (8.14.0)
Requirement already satisfied: importlib-metadata>=1.4 in /Users/guilleaf/Library/Python/3.11/lib/python/site-packages (from watermark) (6.8.0)
Requirement already satisfied: setuptools in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from watermark) (68.2.2)
Requirement already satisfied: zipp>=0.5 in /Users/guilleaf/Library/Python/3.11/lib/python/site-packages (from importlib-metadata>=1.4->watermark) (3.16.2)
Requirement already satisfied: backcall in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (0.2.0)
Requirement already satisfied: decorator in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (5.1.1)
Requirement already satisfied: jedi>=0.16 in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (0.19.1)
Requirement already satisfied: matplotlib-inline in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (0.1.6)
Requirement already satisfied: pickleshare in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (0.7.5)
Requirement already satisfied: prompt-toolkit!=3.0.37,<3.1.0,>=3.0.30 in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (3.0.38)
Requirement already satisfied: pygments>=2.4.0 in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (2.15.1)
Requirement already satisfied: stack-data in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (0.6.2)
Requirement already satisfied: traitlets>=5 in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (5.9.0)
Requirement already satisfied: pexpect>4.3 in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (4.8.0)
Requirement already satisfied: appnope in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (0.1.3)
Requirement already satisfied: parso<0.9.0,>=0.8.3 in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from jedi>=0.16->ipython>=6.0->watermark) (0.8.3)
Requirement already satisfied: ptyprocess>=0.5 in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from pexpect>4.3->ipython>=6.0->watermark) (0.7.0)
Requirement already satisfied: wcwidth in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from prompt-toolkit!=3.0.37,<3.1.0,>=3.0.30->ipython>=6.0->watermark) (0.2.12)
Requirement already satisfied: executing>=1.2.0 in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from stack-data->ipython>=6.0->watermark) (1.2.0)
Requirement already satisfied: asttokens>=2.1.0 in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from stack-data->ipython>=6.0->watermark) (2.2.1)
Requirement already satisfied: pure-eval in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from stack-data->ipython>=6.0->watermark) (0.2.2)
Requirement already satisfied: six in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from asttokens>=2.1.0->stack-data->ipython>=6.0->watermark) (1.16.0)

%%html
<div style="clear: both; display: table;" class="div-white">
  <div style="border: none; float: left; width: 60%; padding: 5px">
  <h1 id="subtitle">Chapter 1. Introduction to Machine Learning</h1>
  <h2 id="subtitle">Guillermo Avendaño Franco<br>Aldo Humberto Romero</h2>
  <br>
  <img src="../fig/1-line logotype124-295.png" alt="Scientific Computing with Python" style="width:50%" align="left">
  </div>
  <div style="border: none; float: left; width: 30%; padding: 5px">
  <img src="../fig/SCPython.png" alt="Scientific Computing with Python" style="width:100%">
  </div>
</div>

Chapter 1. Introduction to Machine Learning

Guillermo Avendaño Franco
Aldo Humberto Romero

Chapter 1. Introduction to Machine Learning

Guillermo Avendaño Franco
Aldo Humberto Romero

Setup

%load_ext watermark

%watermark

Last updated: 2024-08-01T20:51:43.179852-04:00

Python implementation: CPython
Python version       : 3.11.7
IPython version      : 8.14.0

Compiler    : Clang 12.0.0 (clang-1200.0.32.29)
OS          : Darwin
Release     : 20.6.0
Machine     : x86_64
Processor   : i386
CPU cores   : 8
Architecture: 64bit

import time
start = time.time()
chapter_number = 1
import matplotlib
%matplotlib inline
%load_ext autoreload
%autoreload 2
import matplotlib.pyplot as plt

import numpy as np
import matplotlib as mpl
import sklearn

%watermark -iv

matplotlib: 3.8.2
numpy     : 1.26.2
sklearn   : 1.3.0

What is Machine Learning

Machine Learning is a broad subject that intersects mathematics, statistics, computing, and the area of the target application, that being economics, biology, physics, and vision.

One way of encapsulating the domain of Machine Learning is in the context of scientific research. One basic path of how humans started gaining understanding of nature was through observations and experimentation. What experiments and observations do is allow us to gather data. But data alone is not knowledge. Only through generalizations, raw data can be converted into Theories and those theories make predictions that could be corroborated or discredited with new data. In that sort of idea, what Machine Learning is about is producing those generalizations just from the data.

We can do science because nature offers patterns, mathematics is at its core all about patterns and the consequences of logical reasoning on them. Machine Learning also needs patterns without them any new data has nothing to do with previous ones. The only way of making predictions is under the assumption that the future resembles the past.

In the past, we relied on mathematical models, that not only give us insight about nature but also equations that allow us to make predictions. In most cases, clean equations are simply not possible and we have to use numerical approximations but we try to keep the understanding. Machine Learning is used in cases where mathematical models are known, numerical approximations are not feasible, and we We are satisfied with the answers even if we lost the ability to understand why the parameters of Machine Learning models work the way they do.

In summary, we need 3 conditions for using Machine Learning on a problem:

Good data
The existence of patterns on the data
The lack of a good mathematical model to express the patterns present on the data

This workshop is meant to give a quick introduction to some of the techniques one can use to build algorithms for Machine Learning where those 3 conditions are met. Specifically, we will discuss the following sub-fields within machine learning

Classification (for using labeled data to infer labels for unlabelled data)
Anomaly Detection (for finding outliers in a dataset)
Dimensionality Reduction (for analyzing and visualizing high-dimensional datasets)
Clustering (for grouping similar objects in a high dimensional space)

Our experience in solving a problem by using a computer always involves the idea that we have access to the data at the same time that you can define some specific rules that can be used to map an answer. From a programming perspective, you need to create a series of rules that guarantee that given the input you get the correct output. In most cases, the input data is very diverse and the number of rules that needs to be applied to input sequences increases, making the programming scheme fail. A different approach is based on allowing the machine to learn, which means that experience will be used to make accurate predictions. This paradigm can be viewed as:

The Machine Learning approach

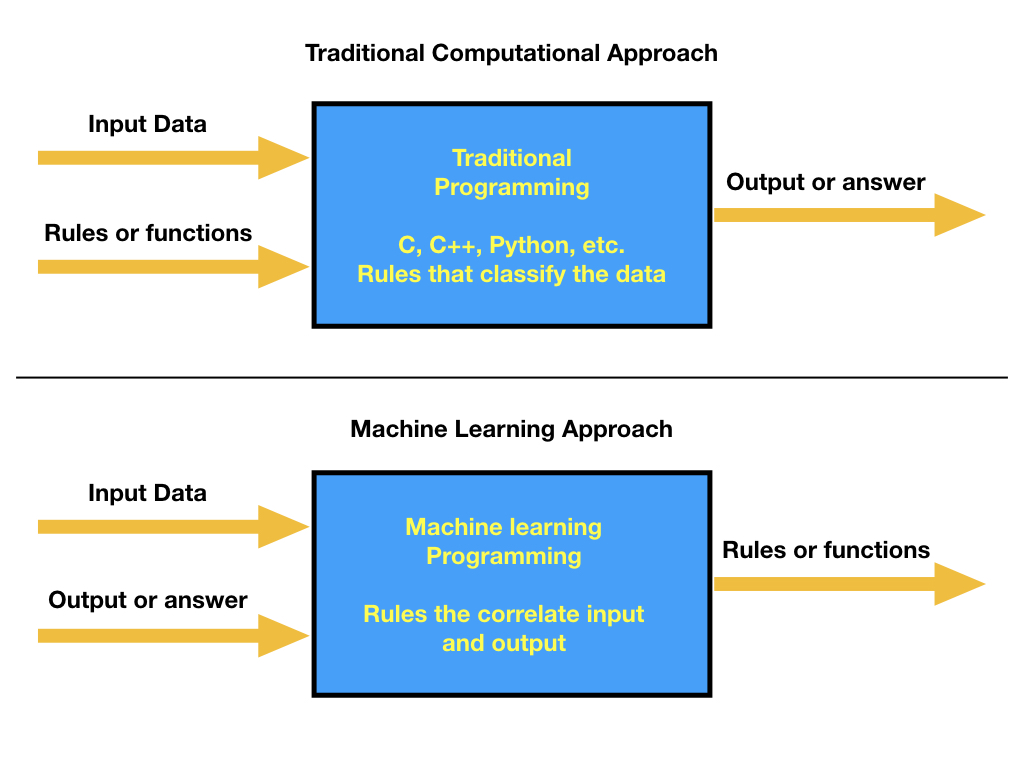
%%html
<img src="../fig/01.MachineLearningParadigm.jpeg" width="500" height="500">

In this new approach of solving problems in the computer, then our concern is to be able to create a model that will take the input and output and, by training a model, meaning allowing the computer to learn and extract the correlations between the provided data, we can find the model parameters that represent the rules and make a prediction (meaning that we can infer the rules in this learning process).

The model parameters can be found by using past information, where the input and output is completely known. Here it is important to stress that the quality and size of the available data is the key to having a very good performance of the machine learning algorithm.

The goal or question that machine learning will try to address needs to be defined. Based on that question, data collection is the most complicated part of any machine learning. This could happen because the data is obtained from different formats, different sources, very old databases, etc. Before the data is used, it needs to be cleaned and formatted (this sounds like a trivial process but it is the most consuming part of the process). Even simple statistical correlations need to be performed across different data sources or constraint checks that guarantee that the data is uniform. Only good quality data would give the right value to the machine learning algorithm. After the data is pruned, the machine learning model needs to be selected. There is not a clear path on that and depends on experience, practice, and availability. In this tutorial, we will discuss a few algorithms, but the methods described here are incomplete and we encourage the attendee to go to the WEB or too technical books to search for more methods.

Taxonomy of Machine Learning Algorithms

There are several ways of classifying the wide field of Machine Learning. Algorithms can be classified by the dimensionality of the input and output if they deal with discrete (categorical) input or output and the basic algorithm underlying the solution. However a classical classification is based on the existence or absents of known output in the problem proposed.

Supervised, Unsupervised and Reinforcement learning

The algorithms of machine learning are generally split into three basic categories: Supervised, Unsupervised, and reinforcement learning.

Supervised Learning

Supervised learning concerns labeled data, and the construction of models that can be used to predict labels for new, unlabeled data. We have access to data that can be classified and labeled previously such that can be used for algorithm training. With the predicted parameters, the algorithm can infer the output from a given input.

Supervised learning algorithms work when the data contains both the inputs and the desired outputs. In this case, predictions can be made for future data where the output is not known.

You can think about these problems as having a set of two sets:

\begin{equation} \left[\; \mathbf{input\ data} \; + \; \mathbf{correct\ result} \; \right] \rightarrow \mathbf{predict\ results\ for\ new\ data} \end{equation}

Example: Given a set of labeled hand-written digits, create an algorithm that will predict the label of a new instance for which a label is not known.

In Supervised Learning, we have a dataset consisting of both features and labels. The task is to construct an estimator which can predict the label of an object given the set of features. A relatively simple example is predicting the species of iris is given a set of measurements of its flower (see next chapter). This is a relatively simple task. Some more complicated examples are:

given a multicolor image of an object through a telescope, determine whether that object is a star, a quasar, or a galaxy.
given a photograph of a person, identify the person in the photo.
given a list of movies a person has watched and their rating of the movie, recommend a list of movies they would like (So-called recommender systems: a famous example is the Netflix Prize).
classify molecules for reactivity

What these tasks have in common is that there is one or more unknown quantities associated with the object which needs to be determined from other observed quantities.

Supervised learning is further broken down into two categories, classification and regression. In classification, the label is discrete, while in regression, the label is continuous.

Unsupervised Learning

Unsupervised learning concerns unlabeled data and finding structure in the data such as clusters, important dimensions, etc. Therefore, unsupervised machine learning algorithms are useful when the available data can not be (or is not) classified or labeled. The methodology will explore the data to infer the correlations or hidden functions from the provided data.

\begin{equation} \left[\; \mathbf{input\ data} \; + \; ? \; \right] \rightarrow \mathbf{discover\ structure\ present\ in\ the\ data} \end{equation}

Unsupervised learning algorithms take a set of data that contains only inputs, no outputs are given and we try to make sense of the data by identifying patterns from them.

Example: Given a set of unlabeled digits, determine which digits are related.

The typical applications of Unsupervised learning are on the clustering of data into groups by similarity and the dimensionality reduction to compress the data while maintaining its structure and usefulness.

A note here is related to the definition of intelligence. It has been pointed out by several researchers that true intelligence will require more independent learning strategies, as we allow the algorithm to explore the data and create awareness by “observing” and “exploring” the data. Therefore, we can say that this learning type is mostly to create autonomous intelligence by rewarding agents for learning about the data.

Now, maybe the simplest goal for unsupervised learning is to train an algorithm that then it can generate its data bases on the learning process. The so-called generative models should be able not only to reproduce the data that we have used to create the model (memorization) but more importantly, to create a more general class on top of the data we have used to train it. For example, after training our algorithm to recognize a face, it should be able to recognize in other environments, different from the ones we have used to train our algorithm.

Reinforcement Learning

Reinforcement learning concerns data with poor knowledge of what the correct results look like, but we can provide a function that grades how good a particular solution should be. These reinforcement machine learning algorithms are methodologies that additionally to the provided data, it can also interact with the environment. This interaction produces actions that can lead to errors or rewards that can maximize the algorithm’s performance. In this methodology, there is no answer but the reinforcement agent decides what to do to perform the given task. In the absence of a training dataset, it is bound to learn from its experience. This methodology is also called active learning and it is now becoming very fancy among practicioners.

Reinforcement learning works in cases where we have inputs, some but not clear output but a reward function that can be used as a guide to know if the model is following a good or bad path. The reward function is used together with the partial data to optimize the outcome under the limited output from the data. This is also called active learning and it is useful for example to define the minimum number of training data it is necessary to use to get very good predictions.

\begin{equation} \left[\; \mathbf{input\ data} \; + \; \mathit{some\ output} \; + \mathbf{grade\ function} \;\right] \rightarrow \mathbf{the\ better\ strategy\ to\ achieve\ a\ solution} \end{equation}

Example: The algorithms used in autonomous vehicles or in learning to play a game against a human opponent.

Words of caution on using Machine Learning

Before we describe some of the used Machine Learning algorithms, I would like to make a small stop and try to make a caution point on the use and development of Machine Learning applications.

It is clear the use of these tools in many different areas, but we also need to be aware that there is the possibility of false positives, blind alleys, and mistakes. The reason is diverse but it can be due to the algorithm’s complexity and errors in the implementation or due to how we manipulate the data. One of the most important error sources is due to the splitting of data. We usually divide the data into training and test sets. In most of our implementations, we use a random distribution for each, but real life is not as random as we think and it is in many cases biased. In real life, data is correlated by different means, for example, we train our model with free data but then use the model into proprietary data. Another example is to use molecules to train a model but then use the model to predict crystal phases.

Another important source of errors comes from how we define the important variables to consider and how sensible are these variables. In most real cases, we try to narrow the number of variables but we need to be aware of how sensible are these variables concerning external agents (temperature, region, modulated external parameters, etc) or other variables. Therefore, sometimes is better to take the time to understand the different variables and try to identify if there are hidden variables that can affect the outcome. A model can not only identify the results but also express the sensibility of the mode. A good way to check the validity of your model is to use different models and different variables.

But from all possible sources of errors, it is important to note that one that can lead to completely wrong conclusions is to define the wrong goal. We can define error measurement by using Loss functions for that specific goal but then, it does not provide enough insight into the actual data. At this point, we just want to strengthen that machine learning practitioners need to spend time with the data, remain close to the data experts to define well-constrained questions and always understand the details of models before you launch any real development.

Now, that we have made some points clear, let us focus on specific applications of Machine Learning.

Classification and Regression

Classification and Regression are closely related problems that are suitable for Supervised Learning Algorithms.

The goal of a classification task is to predict whether a given observation in a dataset possesses some particular property or attribute. To make these predictions, we measure the attributes of several labeled data observations, then compare new unlabelled observations to that measurements.

The goal of regression is to predict a continuous variable (give x, the algorithm should provide f(x)). When the dimensionality of the input is small there are mathematical procedures like Least Squares that are capable of offering results without using Machine Learning, however, when the dimensionality grows and there is not a simple linear relation between the input and the output, Machine Learning Methods are usually the method of choice.

Classification of Science Books

This is a very simple example that captures how Machine Learning Algorithms can classify data. Let’s suppose we have a collection of 200 ebooks; around 50 of them are from biology, another 50 are from chemistry, 50 from physics, and 50 from math. Those 200 ebooks I can classify myself. I open the ebook saw the content and put it in the corresponding folder. Those were manually classified.

Now I downloaded a new collection of 1000 more science ebooks, all of them on a single folder with no classification on their own. Those are 1000 unlabelled ebooks. A classification algorithm can help us use the labeled books to predict which of the new books are from biology, physics, chemistry, or math.

To prepare to classify the new books, let’s suppose we count the number of times the words “life” and “quantum”, “bond”, “theorem” occur in each of our 200 labeled ebooks. We tally up the count of each word for each book, producing a spreadsheet with 200 rows and 4 columns.

In a real application, we will use command line programs that convert “PDF”, “epub” and other ebook formats into text, such that we can use simple methods to count and perform statistics over the words. The problem of reading that data is more a Data Mining, the efficient extraction, and counting of words.

We will replicate this scenario below with some fake data:
X will represent our spreadsheet. Each row represents the counts of the words “life”, “quantum”, “bond” and “theorem” in a single book.
labels contains one value for each row in X: 0 for life, 1 for quantum, 2 for bond and 3 for theorem.

For this, we will use the method make_blobs from SciKit learn. Test datasets are those datasets that let you test a machine learning algorithm or test harness. It needs to have very good statistical properties to allow you to test the methodology you are trying to understand.

The make_blobs() function can be used to generate blobs of points with a Gaussian distribution. You can control how many blobs to generate and the number of samples to generate, as well as a host of other properties.

# import the make_blobs function from the sklearn module/package
from sklearn.datasets import make_blobs

# use the function we imported to generate a matrix with 100 rows and 4 columns
# n_samples=200 specifies the number of rows in the returned matrix
# n_features=4 specifies the number of columns in the returned matrix
# centers=4 specifies the number of centroids, or attraction points, in the returned matrix
# random_state=0 makes the random data generator reproducible
# center_box=(0,20) specifies we want the centers in X to be between 0,20
X, labels = make_blobs(n_samples=200, n_features=4, centers=4, random_state=0,
                       center_box=(2,20), cluster_std=2.0,)

# display the first three rows in X and their genre labels
print(X[:3], '\n\n', labels[:3])

[[12.01611512 16.6847356   0.92339112  1.28793479]
 [10.70906038 18.5605713   1.48384719  6.19326813]
 [10.05299862 17.10744117 10.21792595 10.88472808]] 

 [3 3 0]

As we have 4 words as features, it is not possible to plot in just 2D, but we can plot the counting of 2 words on the same book and associate a color for each type of book.

# create 16 subplots
fig, axes = plt.subplots(nrows=4, ncols=4, sharex=True, sharey=True, figsize=(8,8))

# get the 0th column of the matrix (i.e. counts of the word "life")
life = X[:,0]
# get the 1st column of the matrix (i.e. counts of the word "quantum")
quantum = X[:,1]
# get the 2st column of the matrix (i.e. counts of the word "bond")
bond = X[:,2]
# get the 3st column of the matrix (i.e. counts of the word "theorem")
theorem = X[:,3]

# One dictionary for all of them
data={0: life, 1: quantum, 2: bond, 3: theorem}

# labels
words=['life', 'quantum', 'bond', 'theorem']

# create a "scatterplot" of the data in X
# the first argument to plt.scatter is a list of x-axis values
# the second argument to plt.scatter is a list of y-axis values
# c=labels specifies we want to use the list of labels to color each point
# cmap=plt.cm.RdYlBu specifies we want to use the Red Yellow Blue colors in the chart

colors=np.array(['r', 'g', 'b', 'k'])
colors=colors[labels]

for i in range(4):
    for j in range(4):
        axes[i,j].scatter(data[3-j], data[i], c=colors) #,cmap=plt.cm.RdYlBu)
    axes[3,i].set_xlabel(words[i])
    axes[i,0].set_ylabel(words[3-i])

png

The plot above shows each of our 200 labelled books, positioned according to the counts of the words “life”, “quantum”, “bond” and “theorem” in the book, and colored by the book’s genre label. Biology books are green; Physics books are red, Chemistry are black and Math books are blue. As we can see, the 4 genres appear distinct here, which means we can expect that some classification is possible.

The important thing about the data above is that we know the genre label of each book. In classification tasks, we leverage labelled data in order to make informed predictions about unlabelled data. One of the simplest ways to make this kind of prediction is to use a K-Nearest Neighbor classifier.

K-Nearest Neighbors Classifiers

With a K-Nearest Neighbors Classifier, we start with a labelled dataset (e.g. 200 books with genre labels). We then add new, unlabelled observations to the dataset. For each, we consult the K labelled observations to which the unlabelled observation is closest, where K is an odd integer we use for all classifications. We then find the most common label among those K observations (the “K nearest neighbors”) and give a new observation that label.

The following diagram shows this scenario. Our new observation (represented by the question mark) has some points near it that are labelled with a triangle or star. Suppose we have chosen to use 3 for our value of K. In that case, we consult the 3 nearest labelled points near the question mark. Those 3 nearest neighbors have labels: star, triangle, triangle. Using a majority vote, we give the question mark a triangle label.

Examining the plot above, we can see that if K were set to 1, we would classify the question mark as a star, but if K is 3 or 5, we would classify the question mark as a triangle. That is to say, K is an important parameter in a K Nearest Neighbors classifier.

To show how to execute this classification in Python, let’s show how we can use our labeled book data to classify an unlabelled book:

from sklearn.neighbors import KNeighborsClassifier

areas=np.array(['Chemistry', 'Mathematics', 'Physics', 'Biology'])

count_life=10.0
count_quantum=10.0
count_bond=10.0
count_theorem=20.0

# create a KNN classifier using 3 as the value of K
clf = KNeighborsClassifier(5)

# "train" the classifier by showing it our labelled data
clf.fit(X, labels)

# predict the genre label of a new, unlabelled book
value=clf.predict(np.array([[count_life, count_quantum, count_bond, count_theorem]]))

areas[value][0]

'Mathematics'

For each observation we pass as input to clf.predict(), the function returns one label (from 0 to 3). In the snippet above, we pass in only a single observation, so we get only a single label back. The example observation above gets a label 1, which means the model thought this particular book is about Mathematics. Just like that, we’ve trained a machine learning classifier and classified some new data!

The classification example above shows how we can classify just a single point in the features space, but suppose we want to analyze the way a classifier would classify each possible point in that space or a subspace. To do so, we can transform our space into a grid of units, then classify each point in that grid. Analyzing a space in this way is known as identifying a classifier’s decision boundary, because this analysis shows one of the boundaries between different classification outcomes in the feature space. This kind of analysis is very helpful in training machine learning models because studying a classifier’s decision boundary can help one see how to improve the classifier.

Let’s plot our classifier’s decision boundary below:

print(labels[:10])
chem_labels=(labels!=0).astype(int)
print(len(chem_labels))
chem_labels[:10]

[3 3 0 2 3 0 1 3 0 2]
200

array([1, 1, 0, 1, 1, 0, 1, 1, 0, 1])

from sklearn.neighbors import KNeighborsClassifier

# create and train a KNN model
clf = KNeighborsClassifier(5)
clf.fit(X[:,:2], chem_labels)

KNeighborsClassifier()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

# use a helper function to plot the trained classifier's decision boundary
helpers.plot_decision_boundary(clf, X, chem_labels)

# add a title and axis labels to the chart
plt.title('K-Nearest Neighbors: Classifying Chemistry Books')
plt.xlabel('occurrences of word life')
plt.ylabel('occurrences of word quantum')

Text(0, 0.5, 'occurrences of word quantum')

png

For each pixel in the plot above, we retrieve the 5 closest points with known labels. We then use a majority vote of those labels to assign the label of the pixel. This is exactly analogous to predicting a label for an unlabelled point—in both cases, we take a majority vote of the 5 closest points with known labels. Working in this way, we can use labelled data to classify unlabelled data. That’s all there is to K-Nearest Neighbors classification!

It’s worth noting that K-Nearest Neighbors is only one of many popular classification algorithms. From a high-level point of view, each classification algorithm works in a similar way—each requires a certain number of observations with known labels, and each uses those labeled observations to classify unlabelled observations. However, different classification algorithms use different logic to assign unlabelled observations to groups, which means different classification algorithms have very different decision boundaries. In the chart below [source], each row plots the decision boundaries several classifiers give the same dataset. Notice how some classifiers work better with certain data shapes:

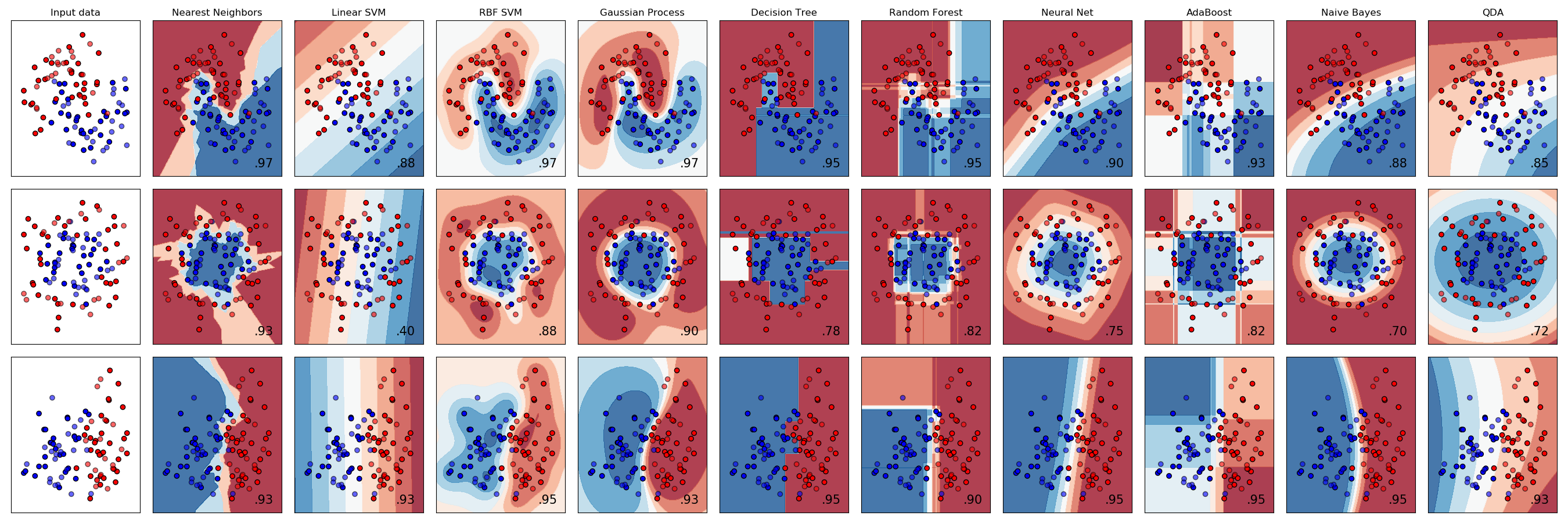
For an intuitive introduction to many of these classifiers, including Support Vector Machines, Decision Trees, Neural Networks, and Naive Bayes classifiers, see the simple introduction by Luis Serrano’s introduction to machine learning video discussed in the Going Further section below.

Naive Bayes Classification

This is maybe one of the most popular methods used for classification as it is one of the most simplest and fastest method. As before, we have a series of features ${x_i}$ and a class ${c_j}$, where $i=1,\cdots,n$, $n$ being the total number of features and $j=1,\cdots , m$, $m$ is the total number of classes. The most important assumption of the Naive Bayes method is to assume that the features are uncorrelated and it is based on the so called Bayes theory, which provides a method to calculate the posterior probability $P(c_i

x_1,x_2,\cdots,x_n)$ from $P(c_j)$, $P(x_1,x_2,\cdots,x_n)$ and

$$P(x_1,x_2,\cdots,x_n

c_j)=P(x_1

c_j)P(x_2

c_j)P(x_3

c_j)\cdots P(x_n

c_j)$$.

This is given by

\begin{equation} P(c_i|x_1,x_2,\cdots,x_n) = \frac{ P(x_1|c_j)P(x_2|c_j)P(x_3|c_j)\cdots P(x_n|c_j) P(c_j)}{P(x_1,x_2,\cdots,x_n)} \end{equation}

where $P(t

x)$ is the posterior probability for target $t$ given the attributes $x$, $P(x

t)$ s the likelihood which is the probability of predictor given target, $P(t)$ is the prior probability that the target is in a given class and $P(x)$ is the prior probability of predictor.

As this theorem could a bit cumbersome to understand, it is easier if we take an example

Let us consider below a training data set of the exercise programming of a person depending on his mude, which provide if the person will do exercise or not. Now, we need to classify whether the person will exercise or not based on his/her mude. Let’s follow the below steps to perform it.

import pandas as pd
d=[['Upset','Yes'],['Upset','Yes'],['Happy','No'],['Sad','Yes'],['Sad','Yes'],['Sad','No'],['Upset','Yes'],['Upset','Yes'],['Happy','No'],['Upset','No'],['Happy','No'],['Sad','Yes'],['Upset','Yes'],['Sad','Yes'],['Happy','Yes']]
data=pd.DataFrame(d,columns=['Mude','Exercise'])
print(data)

     Mude Exercise
 Upset      Yes
 Upset      Yes
 Happy       No
   Sad      Yes
   Sad      Yes
   Sad       No
 Upset      Yes
 Upset      Yes
 Happy       No
 Upset       No
Happy       No
  Sad      Yes
Upset      Yes
  Sad      Yes
Happy      Yes

Now let us calculate the frequency table

pd.crosstab(data['Mude'], [data['Exercise']])

Exercise	No	Yes
Mude
Happy	3	1
Sad	1	4
Upset	1	5

Now let us calculate the probability per each state of possible Mude

rating_probs = data.groupby('Mude').size().div(len(data))
print(rating_probs)

Mude
Happy    0.266667
Sad      0.333333
Upset    0.400000
dtype: float64

Now let us calculate the conditional probabilities

data.groupby(['Mude', 'Exercise']).size().div(len(data)).div(rating_probs, axis=0, level='Mude')

Mude   Exercise
Happy  No          0.750000
       Yes         0.250000
Sad    No          0.200000
       Yes         0.800000
Upset  No          0.166667
       Yes         0.833333
dtype: float64

Now that we have a way to estimate the probability of a given data point falling in a certain class, $P(c_i|x_1,x_2,\cdots,x_n)$, we need to be able to use this to produce classifications. Naive Bayes handles this in as simple as possible; simply pick the c_i that has the largest probability given the data point’s features. If the features are continuous, what we usually do is to model the probability distribution of $P(x_i,c_j)$. Usually a Gaussian distribution is used.

Some of the real uses of this methodology as in spam email classification and news articles classification.

Anomaly Detection

Anomaly detection is the identification of rare items, events or observations which raise suspicions by differing significantly from the majority of the data, the so-called outliers. They can be due to data spurious or they can be real as in bank fraud, medical problems, structural defects, malfunctioning equipment, structural phase transitions, etc. While detecting anomalies in a single dimension can be quite simple, finding anomalies in high-dimensional datasets is a difficult problem.

One technique for classifying anomalies in high-dimensional datasets is an Isolation Forest. An Isolation Forest identifies outliers in a dataset by randomly dividing a space until each point is isolated from the other. After repeating this procedure several times, the Isolation Forest identifies points that are quickly isolated from other points as outliers. Isolation Forest explicitly identifies anomalies instead of profiling normal data points. An anomalous point could be separated in a few steps while normal points which are closer could take significantly more steps to be segregated.

The illustration below attempts to illustrate the method by which these outliers are quickly identified. Isolated points are colored green and labeled with the iteration on which they were isolated. If you repeat the procedure several times, you’ll see the outlier is consistently isolated quickly, which allows the Isolation Forest to identify that point as an outlier.

from IPython.display import IFrame

IFrame(src='https://s3.amazonaws.com/duhaime/blog/visualizations/isolation-forests.html', width=700, height=640)

If we run the simulation above a number of times, we should see the “outlier” point is consistently isolated quickly, while it usually takes more iterations to isolate the other points. This is the chief intuition behind the Isolation Forests outlier classification strategy—outliers are isolated quickly because they are farther from other points in the dataset.

Let’s build a sample dataset and use Isolation Forests to classify the outliers in that dataset.

from sklearn.ensemble import IsolationForest
from sklearn.datasets import make_blobs

# seed a random number generator for consistent random values
rng = np.random.RandomState(1)

# generate 100 "training" data observations
n_training = 500
X, _ = make_blobs(random_state=6, n_samples=n_training)

# create the IsolationForest classifier
clf = IsolationForest(max_samples=500, random_state=1, n_jobs=-1)

# train the classifier on the training data
clf.fit(X)

# generate 100 new observations
new_vals = rng.uniform(low=(-10, -12), high=(10, 4), size=(100, 2))

# get classification results for the new observations; `result` contains
# one observation for each value in `new_vals`: a 1 means the point was
# in the training distribution, -1 means the point is an outlier
result = clf.predict(new_vals)

# plot the classification results
helpers.plot_iforest_decision_boundary(clf, X, new_vals, result)

png

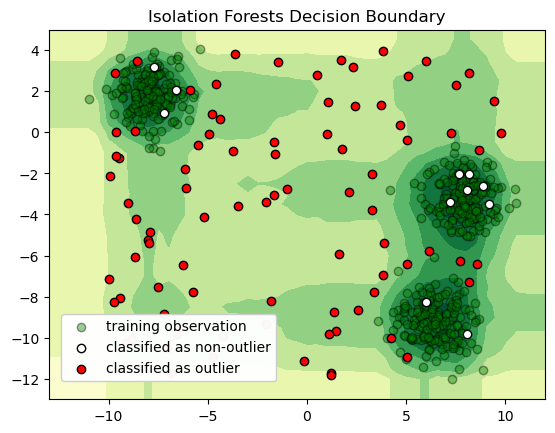
In just a few lines of code, we can create, train, and deploy a machine learning model for detecting outliers in high-dimensional data!

Dimensionality Reduction

In our example above, we used 4 labels (the book type) and 4 words existing in the text (life, quantum, bond, and theorem) to classify new books from the number of occurrences of those words on new books. While each observation in the dataset above has only four components, it is quite challenging to visualize. In more real-world scenarios, the number of features can be tens, hundreds or even thousands of features. We can count more words, we can actually use all the words in those books. The resulting number of features will be on the order of thousands. However, having that extra data does not necessarily mean that the classification will be better, and it can surely make things worst. There are words that are not specific to any discipline so counting its number will be irrelevant. There are other words, like atom that are probably shared in equal numbers by books on Chemistry and Physics so those words will not help either.

“High-dimensional” datasets can be quite hard to work with and also very hard to understand. High dimensional datasets also pose specific challenges to many machine learning models (see The Curse of Dimensionality). To work around these challenges, it’s often helpful to reduce the number of dimensions required to express a given dataset. This proposed reduction is trying to solve two problems. The dimensionality reduction itself and the focus on more relevant features that maximize the probability of successful classifications.

One popular way to reduce the dimensionality of a dataset is to use a technique called Principal Component Analysis. PCA tries to find a lower dimensional representation of a dataset by projecting that dataset down into a smaller dimensional space in a way that minimizes loss of information.

To get an intuition about PCA, suppose you have points in two dimensions, and you wish to reduce the dimensionality of your dataset to a single dimension. To do so, you could find the center of the points then create a line $L$ with a random orientation that passes through that center. One can then project each point onto $L$ such that an imaginary line between the point and $L$ form a right angle. Within this “projection”, each 2D point can be represented with just its position along the 1D $L$, effectively giving us a 1D representation of the point’s position in its original space. Furthermore, we can use the difference between the largest and smallest values of points projected onto $L$ as a measure of the amount of “variance” or “spread” within the data captured in $L$—the greater this spread, the greater the amount of “signal” from the original dataset is represented in the projection. Therefore, PCA tries to maximize the sum of the square distances from the projected points to the “centroid” of the data or the center of the line. Another feature obtained from the analysis is the relative importance of the different variables. From the slope of the line, we can correlate the relevance and importance of the variables. In the example below, if the line has a slope of 0.1, it means that the first variable (along the X-axis) is more sensitive to the measurements than the second variable.

If one were to slowly rotate $L$ and continue measuring the delta between the greatest and smallest values on $L$ at each orientation, one could find the orientation of the projection line that minimizes information loss. (This line of minimal information loss is shown in pink below.) Once that line is discovered, we can actually project all of our points onto that lower-dimensional embedding (see the red points below when the black line is colinear with the pink line):

For a beginner-friendly deep dive into the mechanics behind this form of dimension reduction, check out Josh Starmer’s step-by-step guide to PCA.

What makes this kind of dimension reduction useful for research? There are two primary uses for dimension reduction: data exploration and data analysis.

Clustering

Clustering is a powerful unsupervised machine learning technique, and one that often requires some kind of distance metric. A cluster refers to a collection of data points aggregated together because of certain similarities. Typically, unsupervised algorithms make inferences from datasets using only input vectors without referring to known, or labelled, outcomes.

There are a variety of methods for clustering vectors, including density-based clustering, hierarchical clustering, and centroid clustering. One of the most intuitive and most commonly used centroid-based methods is K-Means Clustering. Given a collection of points in space, K-Means selects K “centroid” points which are equidistant from all points and the other centroids. The target number k is the number of centroids needed to classify the dataset (this value can be optimized but following the reduction in variation as K increases). A centroid is the imaginary or real location representing the center of the cluster. Every data point is allocated to each of the clusters by reducing the in-cluster sum of squares. In practice, we select the positions of the centroids randomly (colored green below), then each data point is assigned to the closest centroid. Using these preliminary groupings, the next step is to find the geometric center of each group (the cluster mean). These group centers become the new centroids, and again each point is assigned to the centroid to which it’s closest. This process continues until centroid movement falls below some minimal movement threshold, after which the clustering is complete. An assessment over the quality is done by calculating the cluster spread. By repeating the process with different initial conditions, we can get a simple approach to identify the lowest spread of all. Here’s a nice visual description of K-Means:

Let’s get a taste of K-means clustering by using the technique to cluster some high-dimensional vectors. For this demo, we can use Stanford University’s GloVe vectors, which provide a vector representation of each word in a corpus. The basic training is performed on aggregated global word-word co-occurrence statistics from a corpus. In what follows below, we’ll read in the GloVe file, split out the first n words and their corresponding 50 dimensional vectors, then examine the first word and its corresponding vector.

from zipfile import ZipFile
from collections import defaultdict
from urllib.request import urlretrieve
import numpy as np
import json, os, codecs

# download the vector files we'll use
if not os.path.isdir("data"):
    os.mkdir("data")
if not os.path.exists('./data/glove.6B.zip'):
  urlretrieve('http://nlp.stanford.edu/data/glove.6B.zip', './data/glove.6B.zip')
# unzip the downloaded zip archive
zf = ZipFile('./data/glove.6B.zip')

zf.filelist

[<ZipInfo filename='glove.6B.50d.txt' compress_type=deflate filemode='-rw-rw-r--' file_size=171350079 compress_size=69182485>,
 <ZipInfo filename='glove.6B.100d.txt' compress_type=deflate filemode='-rw-rw-r--' file_size=347116733 compress_size=134300389>,
 <ZipInfo filename='glove.6B.200d.txt' compress_type=deflate filemode='-rw-rw-r--' file_size=693432828 compress_size=264336891>,
 <ZipInfo filename='glove.6B.300d.txt' compress_type=deflate filemode='-rw-rw-r--' file_size=1037962819 compress_size=394362180>]

data = zf.read("glove.6B.50d.txt").decode("utf-8")

#zf.extract("glove.6B.50d.txt")
#data = codecs.open('glove.6B.50d.txt', 'r', 'utf8')
#os.remove('glove.6B.50d.txt')

# get the first n words and their vectors
vectors = []
words = []
n = 50000
for row_idx, row in enumerate(data.split('\n')):
  if row_idx > n: break
  split_row = row.split()
  word, vector = ' '.join(split_row[:-50]), [float(i) for i in split_row[-50:]]
  words += [word]
  vectors += [vector]

# check out a sample word and its vector
print(words[1700], vectors[1700], '\n')

jersey [-0.58799, 0.5237, -0.43901, 0.20235, -0.24809, 0.83891, -1.8201, -0.24394, -0.042007, -0.88241, -0.31837, -0.62089, -0.065572, -0.23857, -0.43266, -0.22669, -0.48063, -0.25786, -1.0126, -0.43651, -0.32772, -0.31723, -0.78414, 0.2991, -1.4958, -1.8041, 0.053844, 0.62729, -0.044872, -1.3678, 1.4082, 0.52184, -0.15919, -1.0641, 0.63164, -0.66726, -0.1372, 0.26659, 0.57591, -0.65129, -0.34107, -0.015463, 0.56549, 0.096276, -0.6589, 0.37402, -0.22312, -0.67946, 0.27789, 0.51315] 

As we can see above, words is just a list of words. For each of those words, vectors contains a corresponding 50-dimensional vector (or list of 50 numbers). Those vectors indicate the semantic meaning of a word. In other words, if the English language were a 50-dimensional vector space, each word in words would be positioned in that space by virtue of its corresponding vector.

Words that have similar meanings should appear near one another within this vector space. To test this hypothesis, let’s use K-Means clustering to identify 20 clusters of words within the 50-dimensional vector space discussed above. After building a K-Means model, we’ll create a map named groups whose keys will be cluster ids (0-19) and whose values will be lists of words that belong to a given cluster number. After creating that variable, we’ll print the first 10 words from each cluster:

from sklearn.cluster import KMeans

# cluster the word vectors
kmeans = KMeans(n_clusters=20, random_state=0).fit(np.array(vectors))

# `kmeans.labels_` is an array whos `i-th` member identifies the group to which
# the `i-th` word in `words` is assigned
groups = defaultdict(list)
for idx, i in enumerate(kmeans.labels_):
  groups[i] += [words[idx]]

# print the top 10 words contained in each group
selected=0
for i in groups:
  print(groups[i][:10])
  if 'attack' in groups[i]:
    selected=i

['the', ',', '.', 'of', 'to', 'and', 'in', 'a', '"', "'s"]
['percent', '%', 'rose', 'fell', 'index', 'yen', 'cents', 'percentage', 'benchmark', 'jumped']
['$', 'million', 'billion', 'dollars', 'total', 'per', '100', 'average', 'miles', '50']
['company', 'stock', 'shares', '&amp;', 'inc.', 'buy', 'firm', 'corp.', 'co.', 'owned']
['minister', 'leader', 'prime', 'secretary', 'chairman', 'deputy', 'afp', 'quoted', 'premier', 'ambassador']
['police', 'killed', 'israel', 'al', 'army', 'forces', 'troops', 'israeli', 'attack', 'palestinian']
['game', 'season', 'points', 'won', 'games', 'league', 'win', 'played', 'cup', 'round']
['–', 'born', 'died', 'church', 'century', 'son', 'king', 'published', 'ii', 'st.']
['/', 'e', 'p.m.', '=', 'magazine', 'mail', 'journal', 'ap', 'x', 'editor']
['john', 'george', 'david', 'michael', 'james', 'robert', 'paul', 'william', 'lee', 'daughter']
['town', 'near', 'district', 'county', 'river', 'park', 'village', 'located', 'airport', 'lake']
['de', 'spain', 'la', 'el', 'francisco', 'argentina', 'jose', 'jean', 'madrid', 'santa']
['water', 'species', 'plant', 'hot', 'ice', 'rice', 'plants', 'bowl', 'fish', 'leaves']
['drug', 'heart', 'cause', 'disease', 'treatment', 'blood', 'drugs', 'patients', 'cancer', 'doctors']
['love', 'character', 'songs', 'god', 'girl', 'guy', 'novel', 'artist', 'musical', 'characters']
['charges', 'justice', 'judge', 'rules', 'constitution', 'ban', 'supreme', 'denied', 'illegal', 'filed']
['systems', 'software', 'type', 'optional', 'c', 'structure', 'uses', 'engine', 'simple', 'digital']
['blue', 'feet', 'floor', 'bus', 'streets', 'door', 'covered', 'foot', 'stone', 'steel']
['fears', 'poverty', 'recession', 'tensions', 'risks', 'racial', 'blame', 'extreme', 'calm', 'emotional']
['ah', 'oh', 'ee', 'uh', 'hah', 'dee', 'ahl', 'tee', 'kah', 'nee']

Notice for example this case (GloVe 6B was created from Wikipedia 2014, it is not updated with current world events)

for i in range(10):
  for j in range(5):
    print("%15s" % groups[selected][i+10*j],end='')
  print("")

         police       southern       fighting           arab       conflict
         killed        attacks        eastern          armed        taliban
         israel       northern    afghanistan      coalition   independence
             al       province        accused         turkey      terrorist
           army       pakistan       arrested           gaza      militants
         forces       soldiers           nato         muslim        wounded
         troops          iraqi        islamic           camp         ethnic
        israeli       violence        injured   palestinians          fired
         attack         border         rebels           bomb      indonesia
    palestinian           dead        killing        baghdad     supporters

The output above shows the top 10 words in each of the 20 clusters identified by K-Means. Examining each of these word lists, we can see each has a certain topical coherence. For example, some of the word clusters contain financial words, while others contain medical words. These clusters work out nicely because K-Means is able to cluster nearby word vectors in our vector space!

Loss Functions in Machine Learning

In reality, machines learn by means of a loss function. This function evaluates how the created model fits the given data. As we optimize our procedure, the loss function is able to reduce the prediction error. Before, we go specifically into some models of Machine Learning, let me give you some details about the used loss functions.

1) Mean Square Error (MSE). This function measures the average of squared difference between predictions and actual observations as

\begin{equation} \text{MSE} = \frac{\sum^N (y_i - \hat{y}_i)^2}{N} \end{equation}

where $N$ is the total available data, $\hat{y}$ is the predicted outcome and $y$ is the actual result.

2) Mean Absolute Error (MAE). This function measures the average of sum of absolute differences between predictions and actual observations. MAE is more robust to outliers since it does not make use of the square function, which penalize these differences.

\begin{equation} \text{MSE} = \frac{\sum^N |y_i - \hat{y}_i|}{N} \end{equation}

3) Hinge Loss/Multi class Loss. It is useful for classification problems and it is based on the assumption that the score of the correct category should be greater than the sum of the scores of all incorrect categories by some safety margin.

\begin{equation} \text{SVMLoss}i = \sum{j \neq y_i} \max(0, s_j - s_{y_i} +1) \end{equation}

where $s_j$ is a scoring of a particular data for the $j$ class, $SVMLoss_i$ is the loss for the $i-$data point, $y_i$ is the true class and the sum is performed over all possible classes.

4) Cross Entropy Loss/Negative Log Likelihood. This method uses the idea of information or entropy as the main function and increases as the predicted probability diverges from the actual label.

\begin{equation} \text{CrossEntropyLoss} = - \left( y_i \log \hat{y_i} + (1- y_i) \log ( 1- \hat{y_i} ) \right) \end{equation}

Acknowledgments

This notebook is based on a variety of sources, usually other notebooks, the material was adapted to the topics covered during lessons. In some cases, the original notebooks were created for Python 2.x or older versions of Scikit-learn or Tensorflow and they have to be adapted to at least Python 3.7.

We acknowledge the support of the National Science Foundation and the US Department of Energy under projects: DMREF-NSF 1434897, NSF OAC-1740111 and DOE DE-SC0016176 is recognized.

References

The snippets above are meant only to give a brief introduction to some of the most popular techniques in machine learning so you can decide whether this kind of analysis might be useful in your research. If it seems like machine learning will be important in your work, you may want to check out some of the resources listed below (arranged roughly from least to most technical):

This list is by no means an exhaustive list of books and resources. I am listing the books from which I took inspiration. Also, I am listing materials where I found better ways to present topics. Often I am amazed by how people can create approachable materials for seemingly dry subjects.

The order of the books goes from divulgation and practical to the more rigorous and mathematical. Slides, blogs, and videos are those I have found over the internet or suggested by others.

Selection of Books on Machine Learning

Hands-On Machine Learning with Scikit-Learn and TensorFlow (First Edition [There is a second edition])
Auréleien Géron
2017

Machine Learning, a Probabilistic Perspective
Sebastian Raschka and Vahid Mirjalili
2017

Foundations of Machine Learning (Second Edition)
Mehryar Mohri, Afshin Rostamizadeh and Ameet Talwalkar
2018

Introduction to Machine Learning - Alpaydin

Introduction to Machine Learning (Fourth Edition)
Ethem Alpaydin
2020

Machine Learning, a Probabilistic Perspective - Murphy

Machine Learning, a Probabilistic Perspective
Kevin P. Murphy
2012

Elements of Statistical Learning - Hastie

Elements of Statistical Learning
Trevor Hastie, Robert Tibshirani, and Jerome Friedman
2008

Jupyter Notebooks

Yale Digital Humanities Lab
Aurelien Geron Hands-on Machine Learning with Scikit-learn First Edition and Second Edition
A progressive collection notebooks of the Machine Learning course by the University of Turin
A curated set of jupyter notebooks about many topics

Videos

In this 30-minute video, Luis Serrano (head of machine learning at Udacity) offers intuitive, user-friendly introductions to the mechanics that drive several machine learning models, including Naive Bayes, Decision Tree, Logistic Regression, Neural Network, and Support Vector Machine classifiers. This video is a great place to start for those looking for quick intuitions about the ways these algorithms work.

Hands-On Machine Learning with Scikit-Learn and TensorFlow (OREILLY)

This OREILLY book offers a great high-level introduction to machine learning with Python. Aurélien Géron guides readers through ways one can use scikit-learn and other popular libraries to build machine learning models in Python. This is a great choice for those who just want to get work done, without necessarily unlocking the insights that would allow one to build models from scratch.

Machine Learning Cheatsheets

This collection of “cheat sheets” gives concise overviews of the API’s and models behind many of the most prominent packages and concepts in machine learning and its allied fields, including different neural network architectures, numerical optimization techniques, algorithms appropriate for different tasks, scikit-learn, pandas, scikit-learn, scipy, ggpot2, dplyr and tidyr, big O notation, and several other topics. Recently identified as the “most popular” article on machine learning in Medium.

Mining of Massive Datasets

This Stanford University course and digital publication offer introductions to a wide array of subtopics in machine learning. The authors focus on helping readers gain an intuitive understanding of how machine learning models work. One of the most lucid and concise treatments of machine learning available on the web.

Convolutional Neural Networks for Visual Recognition

This Stanford University course offers a spectacular introduction to Convolutional Neural Networks, the cornerstone of modern machine learning in the domain of computer vision. If your work involves images or video materials, and you’d like to apply machine learning techniques to your data, this course will help you get up and running with state-of-the-art techniques in convnets.

Machine Learning (Andrew Ng, Coursera)

Andrew Ng’s Coursera course on machine learning will help you master many of the fundamentals involved in modern machine learning. Professor Ng will guide you through a great deal of the math involved in contemporary machine learning, starting with simple linear classifiers and building up into complex neural network architectures. This class is ideal for those who like to understand the math behind the models they use.

Back of the Book

plt.figure(figsize=(3,3))
n = chapter_number
maxt=(2*(n-1)+3)*np.pi/2
t = np.linspace(np.pi/2, maxt, 1000)
tt= 1.0/(t+0.01)
x = (maxt-t)*np.cos(t)**3
y = t*np.sqrt(np.abs(np.cos(t))) + np.sin(0.3*t)*np.cos(2*t)
plt.plot(x, y, c="green")
plt.axis('off');

png

end = time.time()
print(f'Chapter {chapter_number} run in {int(end - start):d} seconds')

Chapter 1 run in 179 seconds

Key Points

tmux allows you to keep terminal sessions on the cluster that persist in case of network disconnection.

Introduction to Deep Learning

Overview

Teaching: 60 min
Exercises: 30 min

Topics

What is Machine Learning?

How I can use tmux?

Objectives

Learn about Sessions, Windows and Panes

Machine Learning for Scientists in a hurry

Boilerplate

!if [ ! -f helpers.py ]; then wget "https://raw.githubusercontent.com/romerogroup/Notebooks_4SIAH/main/Machine_Learning/helpers.py"; fi

# import some custom helper code
import helpers
from helpers import set_css_in_cell_output
get_ipython().events.register('pre_run_cell', set_css_in_cell_output)

!pip install watermark

Defaulting to user installation because normal site-packages is not writeable
Requirement already satisfied: watermark in /Users/guilleaf/Library/Python/3.11/lib/python/site-packages (2.4.3)
Requirement already satisfied: ipython>=6.0 in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from watermark) (8.14.0)
Requirement already satisfied: importlib-metadata>=1.4 in /Users/guilleaf/Library/Python/3.11/lib/python/site-packages (from watermark) (6.8.0)
Requirement already satisfied: setuptools in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from watermark) (68.2.2)
Requirement already satisfied: zipp>=0.5 in /Users/guilleaf/Library/Python/3.11/lib/python/site-packages (from importlib-metadata>=1.4->watermark) (3.16.2)
Requirement already satisfied: backcall in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (0.2.0)
Requirement already satisfied: decorator in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (5.1.1)
Requirement already satisfied: jedi>=0.16 in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (0.19.1)
Requirement already satisfied: matplotlib-inline in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (0.1.6)
Requirement already satisfied: pickleshare in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (0.7.5)
Requirement already satisfied: prompt-toolkit!=3.0.37,<3.1.0,>=3.0.30 in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (3.0.38)
Requirement already satisfied: pygments>=2.4.0 in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (2.15.1)
Requirement already satisfied: stack-data in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (0.6.2)
Requirement already satisfied: traitlets>=5 in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (5.9.0)
Requirement already satisfied: pexpect>4.3 in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (4.8.0)
Requirement already satisfied: appnope in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from ipython>=6.0->watermark) (0.1.3)
Requirement already satisfied: parso<0.9.0,>=0.8.3 in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from jedi>=0.16->ipython>=6.0->watermark) (0.8.3)
Requirement already satisfied: ptyprocess>=0.5 in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from pexpect>4.3->ipython>=6.0->watermark) (0.7.0)
Requirement already satisfied: wcwidth in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from prompt-toolkit!=3.0.37,<3.1.0,>=3.0.30->ipython>=6.0->watermark) (0.2.12)
Requirement already satisfied: executing>=1.2.0 in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from stack-data->ipython>=6.0->watermark) (1.2.0)
Requirement already satisfied: asttokens>=2.1.0 in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from stack-data->ipython>=6.0->watermark) (2.2.1)
Requirement already satisfied: pure-eval in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from stack-data->ipython>=6.0->watermark) (0.2.2)
Requirement already satisfied: six in /opt/local/Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from asttokens>=2.1.0->stack-data->ipython>=6.0->watermark) (1.16.0)

%%html
<div style="clear: both; display: table;" class="div-1">
  <div style="border: none; float: left; width: 60%; padding: 5px">
  <h1 id="subtitle">Chapter 2. The Iris Classification Problem</h1>
  <h2 id="subtitle">Guillermo Avendaño Franco<br>Aldo Humberto Romero</h2>
  <br>
  <img src="../fig/1-line%20logotype124-295.png" alt="Scientific Computing with Python" style="width:50%" align="left">
  </div>
  <div style="border: none; float: left; width: 30%; padding: 5px">
  <img src="../fig/SCPython.png" alt="Scientific Computing with Python" style="width:100%">
  </div>
</div>

Chapter 2. The Iris Classification Problem

Guillermo Avendaño Franco
Aldo Humberto Romero

Chapter 2. The Iris Classification Problem

Guillermo Avendaño Franco
Aldo Humberto Romero

Setup

%load_ext watermark

%watermark

Last updated: 2024-08-01T20:52:10.629385-04:00

Python implementation: CPython
Python version       : 3.11.7
IPython version      : 8.14.0

Compiler    : Clang 12.0.0 (clang-1200.0.32.29)
OS          : Darwin
Release     : 20.6.0
Machine     : x86_64
Processor   : i386
CPU cores   : 8
Architecture: 64bit

import time
start = time.time()
chapter_number = 2
import matplotlib
%matplotlib inline
%load_ext autoreload
%autoreload 2
import matplotlib.pyplot as plt

import numpy as np
import sklearn

%watermark -iv

sklearn   : 1.3.0
numpy     : 1.26.2
matplotlib: 3.8.2

The Anderson’s Iris Dataset
Handwritten Digits Data Set

The Anderson’s Iris Dataset

The Iris flower data set or Fisher’s Iris dataset or Anderson’s Iris Dataset is a multivariate data set introduced by the British statistician and biologist Ronald Fisher in his 1936 paper “The use of multiple measurements in taxonomic problems as an example of linear discriminant analysis.

It is also called Anderson’s Iris data set because Edgar Anderson collected the data to quantify the morphologic variation of Iris flowers of three related species. Two of the three species were collected in the Gaspé Peninsula

To emphasise the quality of the data acquired, he wrote:

“all from the same pasture, and picked on the same day and measured at the same time by the same person with the same apparatus”.

The data set consists of $50$ samples from each of three species of Iris (Iris setosa, Iris virginica and Iris versicolor). With 3 sets of $50$ samples the dataset contains $150$ instances of iris flowers all collected in Hawaii.

Four features were measured from each sample: the length and the width of the sepals and petals, in centimeters. Based on the combination of these four features, Fisher developed a linear discriminant model to distinguish the species from each other.

Fisher’s paper was published in the Annals of Eugenics, the old name of the now called Annals of Human Genetics and includes a discussion of the contained techniques’ applications to the field of phrenology. There is a dark side behind the journal and the role of Ronald Fisher in the area of Eugenics.

Ronald Fisher was not the only contributor to the journal, but he also became editor of Annals of Eugenics a scientific journal that advocates for practices that aim to improve the genetic quality of a human population.

Ronald Fisher himself, held strong views on race and eugenics, insisting on racial differences. In his own words: “Available scientific knowledge provides a firm basis for believing that the groups of mankind differ in their innate capacity for intellectual and emotional development”. All this is an example of how techniques used today in Machine Learning have roots in past and for good or bad will change our future.

The Iris dataset is by far the earliest and the most commonly used in the literature on pattern recognition and today’s Machine Learning.


Iris Setosa	Iris Versicolor	Iris Virginica

Each flower is distinguished based on 4 measures of sepal’s width and length, and petal’s width and length. These measures are taken for each iris flower:

Iris Setosa

Detailed information of the dataset is listed next:

4 features with numerical values, with no missing data
    sepal length in cm
    sepal width in cm
    petal length in cm
    petal width in cm
3 classes, including Iris Setosa, Iris Versicolour, Iris Virginica
data size: 150 entries
data distribution: 50 entries for each class

There are numerous technical papers that use Iris dataset. Here is a partial list:

Fisher,R.A. The use of multiple measurements in taxonomic problems Annual of Eugenics, 7, Part II, 179-188 (1936); also in “Contributions to Mathematical Statistics” (John Wiley, NY, 1950).
Duda,R.O., & Hart,P.E. Pattern Classification and Scene Analysis (1973) (Q327.D83) John Wiley & Sons. ISBN 0-471-22361-1. See page 218.
Dasarathy, B.V. Nosing Around the Neighborhood: A New System Structure and Classification Rule for Recognition in Partially Exposed Environments. (1980) IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. PAMI-2, No. 1, 67-71.
Gates, G.W. The Reduced Nearest Neighbor Rule. (1972) IEEE Transactions on Information Theory, May 1972, 431-433.

In the dataset, Iris Setosa is easier to be distinguished from the other two classes, while the other two classes are partially overlapped and harder to be separated.

More information about this data set and its historical roots:

On Iris flower data set
On Ronald Fisher
On Eugenics
Description of Iris Dataset by Roger Jang as part of an online book on Data Clustering and Pattern Recognition

The purpose of this notebook is to use the Iris dataset to explore several of the methods used in Machine Learning.

For doing that we will use one popular package in Python called Scikit-learn

Representation of Data

Most machine learning algorithms implemented in scikit-learn expect data to be stored in a two-dimensional array or matrix. The arrays can be either numpy.ndarray, or in some cases scipy.sparse matrices. The size of the array is expected to be [n_samples, n_features]

n_samples: The number of samples: each sample is an item to process (e.g. classify). A sample can be a document, a picture, a sound, a video, an astronomical object, a row in database or CSV file, or whatever you can describe with a fixed set of quantitative traits.
n_features: The number of features or distinct traits that can be used to describe each item in a quantitative manner. Features are generally real-valued, but may be boolean or discrete-valued in some cases.

The number of features must be fixed in advance. However it can have a large dimension (e.g. millions of features) with most of them being zeros for a given sample. This is a case where scipy.sparse matrices can be useful, in that they are much more memory-efficient than numpy arrays.

A classification algorithm, for example, expects the data to be represented as a feature matrix and a label vector:

[{\rm feature~matrix:~~~} {\bf X}~=~\left[ \begin{matrix} x_{11} & x_{12} & \cdots & x_{1D}
x_{21} & x_{22} & \cdots & x_{2D}
x_{31} & x_{32} & \cdots & x_{3D}
\vdots & \vdots & \ddots & \vdots
\vdots & \vdots & \ddots & \vdots
x_{N1} & x_{N2} & \cdots & x_{ND}
\end{matrix} \right]]

[{\rm label~vector:~~~} {\bf y}~=~ [y_1, y_2, y_3, \cdots y_N]]

Here there are $N$ samples and $D$ features.

Loading the Iris Data with Scikit-Learn

Scikit-learn has a very straightforward set of data on these iris species. The data consist of The following:

Features in the Iris dataset:
1. sepal length in cm
2. sepal width in cm
3. petal length in cm
4. petal width in cm
Target classes to predict:
1. Iris Setosa
2. Iris Versicolour
3. Iris Virginica

scikit-learn embeds a copy of the iris CSV file along with a helper function to load it into NumPy arrays:

from sklearn.datasets import load_iris
iris = load_iris()

The dataset from scikit-learn is well organized into a dictionary

iris.keys()

dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module'])

print(iris.DESCR)

.. _iris_dataset:

Iris plants dataset
--------------------

**Data Set Characteristics:**

    :Number of Instances: 150 (50 in each of three classes)
    :Number of Attributes: 4 numeric, predictive attributes and the class
    :Attribute Information:
        - sepal length in cm
        - sepal width in cm
        - petal length in cm
        - petal width in cm
        - class:
                - Iris-Setosa
                - Iris-Versicolour
                - Iris-Virginica
                
    :Summary Statistics:

    ============== ==== ==== ======= ===== ====================
                    Min  Max   Mean    SD   Class Correlation
    ============== ==== ==== ======= ===== ====================
    sepal length:   4.3  7.9   5.84   0.83    0.7826
    sepal width:    2.0  4.4   3.05   0.43   -0.4194
    petal length:   1.0  6.9   3.76   1.76    0.9490  (high!)
    petal width:    0.1  2.5   1.20   0.76    0.9565  (high!)
    ============== ==== ==== ======= ===== ====================

    :Missing Attribute Values: None
    :Class Distribution: 33.3% for each of 3 classes.
    :Creator: R.A. Fisher
    :Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
    :Date: July, 1988

The famous Iris database, first used by Sir R.A. Fisher. The dataset is taken
from Fisher's paper. Note that it's the same as in R, but not as in the UCI
Machine Learning Repository, which has two wrong data points.

This is perhaps the best known database to be found in the
pattern recognition literature.  Fisher's paper is a classic in the field and
is referenced frequently to this day.  (See Duda & Hart, for example.)  The
data set contains 3 classes of 50 instances each, where each class refers to a
type of iris plant.  One class is linearly separable from the other 2; the
latter are NOT linearly separable from each other.

.. topic:: References

   - Fisher, R.A. "The use of multiple measurements in taxonomic problems"
     Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to
     Mathematical Statistics" (John Wiley, NY, 1950).
   - Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.
     (Q327.D83) John Wiley & Sons.  ISBN 0-471-22361-1.  See page 218.
   - Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System
     Structure and Classification Rule for Recognition in Partially Exposed
     Environments".  IEEE Transactions on Pattern Analysis and Machine
     Intelligence, Vol. PAMI-2, No. 1, 67-71.
   - Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule".  IEEE Transactions
     on Information Theory, May 1972, 431-433.
   - See also: 1988 MLC Proceedings, 54-64.  Cheeseman et al"s AUTOCLASS II
     conceptual clustering system finds 3 classes in the data.
   - Many, many more ...

iris.feature_names

['sepal length (cm)',
 'sepal width (cm)',
 'petal length (cm)',
 'petal width (cm)']

iris.target_names

array(['setosa', 'versicolor', 'virginica'], dtype='<U10')

n_samples, n_features = iris.data.shape
print("Number of Samples:", n_samples)
print("Number of features:", n_features)

Number of Samples: 150
Number of features: 4

Both data and target are objects numpy.ndarray with the shapes below

print(type(iris.data))
print(iris.data.shape)
print(iris.target.shape)

<class 'numpy.ndarray'>
(150, 4)
(150,)

One example from the first 5 elements, each row is one entry:

iris.data[:5]

array([[5.1, 3.5, 1.4, 0.2],
       [4.9, 3. , 1.4, 0.2],
       [4.7, 3.2, 1.3, 0.2],
       [4.6, 3.1, 1.5, 0.2],
       [5. , 3.6, 1.4, 0.2]])

The target contains 150 digits corresponding to the 3 classes of Iris flowers

print (iris.target)

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2]

This data is four-dimensional, but we can visualize two of the dimensions at a time using a simple scatter-plot:

x_index = 2
y_index = 3

# this formatter will label the colorbar with the correct target names
formatter = plt.FuncFormatter(lambda i, *args: iris.target_names[int(i)])

plt.scatter(iris.data[:, x_index], iris.data[:, y_index],
            c=iris.target)
plt.colorbar(ticks=[0, 1, 2], format=formatter)
plt.xlabel(iris.feature_names[x_index])
plt.ylabel(iris.feature_names[y_index]);

png

All the relations can be shown as a grid of 4x4 subplots in matplotlib

# this formatter will label the colorbar with the correct target names
formatter = plt.FuncFormatter(lambda i, *args: iris.target_names[int(i)])
fig, axes=plt.subplots(nrows=4, ncols=4, figsize=(16,16))

for i in range(4):
    for j in range(4):
        axes[i,j].scatter(iris.data[:, j], iris.data[:, i], c=iris.target)
        if i==3: axes[i,j].set_xlabel(iris.feature_names[j])
        if j==0: axes[i,j].set_ylabel(iris.feature_names[i]);

#plt.colorbar(ticks=[0, 1, 2], format=formatter)

png

From the figure is clear that setosa variety is fairly separated from the versicolor and virginica and those two in turn are difficult to separate but for some features the distinction is clear.

Classification (Logistic Regression)

Logistic regression is a statistical method that is used to analyze datasets in which there are one or more independent variables that determine a binary outcome (True/False, 1/0). The goal of this methodology is to find the best fitting model to describe the relationship between the independent input variables and the dichotomous outcome. The probability distribution would have the form of an s-shape as:

[\log \left( \frac{p}{1-p} \right) = a + b_1 x_1 + b_2 x_2 \cdots]

where p is the probability of presence of the characteristic of interest, $x_1, x_2, \cdots$ are the independent input variables and $a, b_1, b_2, \cdots$ are the model fitted parameters. As here we want to optimize the probability distribution, we do not use the square error minimization but to maximize the likelihood of observing the sample values. This statistical process can be found in many different machine learning books or Logistic Regression lecture.

X = iris["data"][:, 3:]  # petal width
y = (iris["target"] == 2).astype(np.int64)  # 1 if Iris-Virginica, else 0

Note: LogisticRegression implements several solvers such as “liblinear”, “newton-cg”, “lbfgs”, “sag” and “saga”. “lbfgs” is used to converge faster on high-dimensional data. In reality, 4 dimensions are not really high-dimensional.

from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(solver="lbfgs", random_state=42)
log_reg.fit(X, y)

LogisticRegression(random_state=42)

X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)

plt.plot(X_new, y_proba[:, 1], "g-", linewidth=2, label="Iris-Virginica")
plt.plot(X_new, y_proba[:, 0], "b--", linewidth=2, label="Not Iris-Virginica")

[<matplotlib.lines.Line2D at 0x144785b90>]

png

X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
decision_boundary = X_new[y_proba[:, 1] >= 0.5][0]

decision_boundary[0]

1.6606606606606606

We can add more to the plot to show how samples are classified under our logistic curve.

plt.figure(figsize=(10, 6))
plt.plot(X[y==0], y[y==0], "bs")
plt.plot(X[y==1], y[y==1], "g^")
plt.plot([decision_boundary, decision_boundary], [-1, 2], "k:", linewidth=2)
plt.plot(X_new, y_proba[:, 1], "g-", linewidth=2, label="Iris-Virginica")
plt.plot(X_new, y_proba[:, 0], "b--", linewidth=2, label="Not Iris-Virginica")
plt.text(decision_boundary+0.02, 0.15, "Decision  boundary", fontsize=14, color="k", ha="center")
plt.arrow(decision_boundary[0], 0.08, -0.3, 0, head_width=0.05, head_length=0.1, fc='b', ec='b')
plt.arrow(decision_boundary[0], 0.92, 0.3, 0, head_width=0.05, head_length=0.1, fc='g', ec='g')
plt.xlabel("Petal width (cm)", fontsize=14)
plt.ylabel("Probability", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.axis([0, 3, -0.02, 1.02]);

png

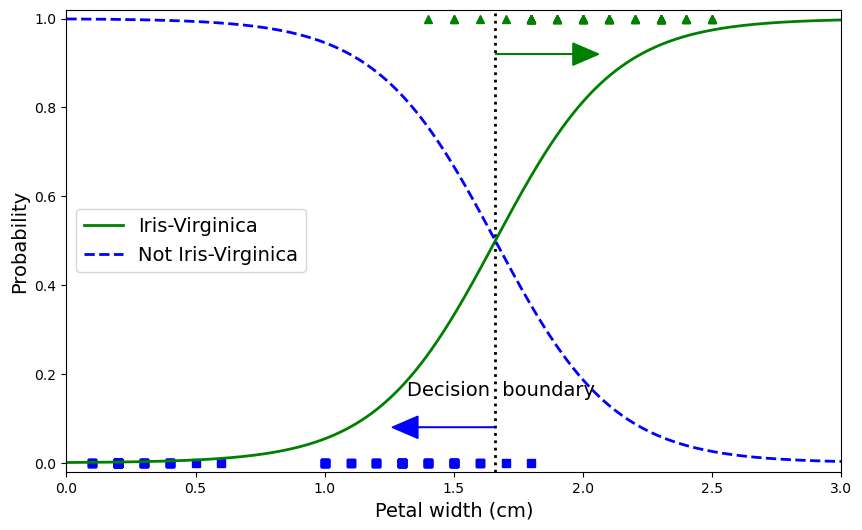
decision_boundary

array([1.66066066])

log_reg.predict([[1.7], [1.5]])

array([1, 0])

from sklearn.linear_model import LogisticRegression

X = iris["data"][:, (2, 3)]  # petal length, petal width
y = (iris["target"] == 2).astype(np.int64)

log_reg = LogisticRegression(solver="lbfgs", C=10**10, random_state=42)
log_reg.fit(X, y)

x0, x1 = np.meshgrid(
        np.linspace(2.9, 7, 500).reshape(-1, 1),
        np.linspace(0.8, 2.7, 200).reshape(-1, 1),
    )
X_new = np.c_[x0.ravel(), x1.ravel()]

y_proba = log_reg.predict_proba(X_new)

plt.figure(figsize=(10, 6))
plt.plot(X[y==0, 0], X[y==0, 1], "bs")
plt.plot(X[y==1, 0], X[y==1, 1], "g^")

zz = y_proba[:, 1].reshape(x0.shape)
contour = plt.contour(x0, x1, zz, cmap=plt.cm.brg)


left_right = np.array([2.9, 7])
boundary = -(log_reg.coef_[0][0] * left_right + log_reg.intercept_[0]) / log_reg.coef_[0][1]

plt.clabel(contour, inline=1, fontsize=12)
plt.plot(left_right, boundary, "k--", linewidth=3)
plt.text(3.5, 1.5, "Not Iris-Virginica", fontsize=14, color="b", ha="center")
plt.text(6.5, 2.3, "Iris-Virginica", fontsize=14, color="g", ha="center")
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.axis([2.9, 7, 0.8, 2.7]);

png

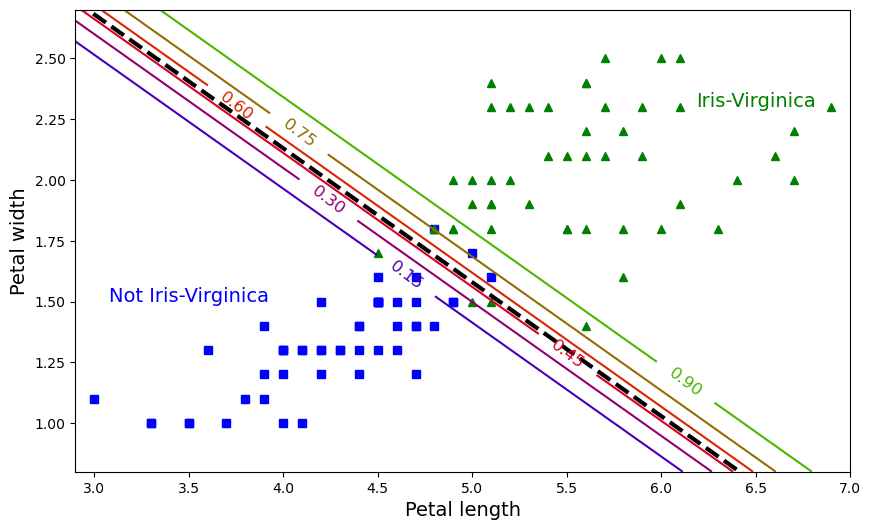
X = iris["data"][:, (2, 3)]  # petal length, petal width
y = iris["target"]

softmax_reg = LogisticRegression(multi_class="multinomial", solver="lbfgs", C=10, random_state=42)
softmax_reg.fit(X, y)

LogisticRegression(C=10, multi_class='multinomial', random_state=42)

# logistic but 3 classes, where the largest is defined by the statistical analysis of occurrence
# of the training data
x0, x1 = np.meshgrid(
        np.linspace(0, 8, 500).reshape(-1, 1),
        np.linspace(0, 3.5, 200).reshape(-1, 1),
    )
X_new = np.c_[x0.ravel(), x1.ravel()]


y_proba = softmax_reg.predict_proba(X_new)
y_predict = softmax_reg.predict(X_new)

zz1 = y_proba[:, 1].reshape(x0.shape)
zz = y_predict.reshape(x0.shape)

plt.figure(figsize=(10, 4))
plt.plot(X[y==2, 0], X[y==2, 1], "g^", label="Iris-Virginica")
plt.plot(X[y==1, 0], X[y==1, 1], "bs", label="Iris-Versicolor")
plt.plot(X[y==0, 0], X[y==0, 1], "yo", label="Iris-Setosa")

from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])

plt.contourf(x0, x1, zz, cmap=custom_cmap)
contour = plt.contour(x0, x1, zz1, cmap=plt.cm.brg)
plt.clabel(contour, inline=1, fontsize=12)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.axis([0, 7, 0, 3.5])

(0.0, 7.0, 0.0, 3.5)

png

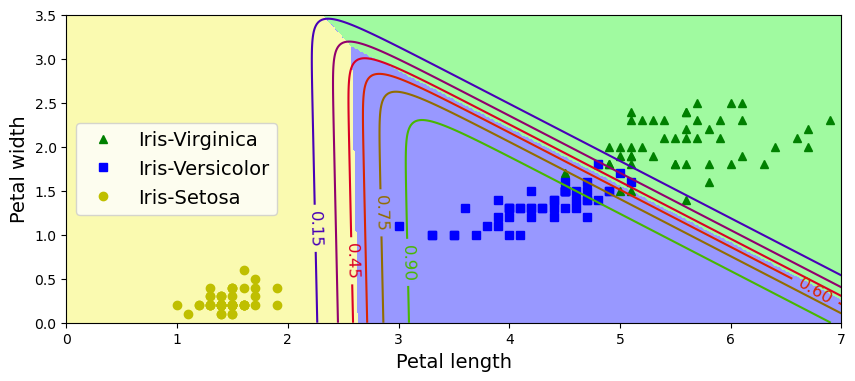
softmax_reg.predict([[5, 2]])

array([2])

softmax_reg.predict_proba([[5, 2]])

array([[6.38014896e-07, 5.74929995e-02, 9.42506362e-01]])

The Scikit-learn estimator, transformations and pipelines

Every algorithm is exposed in scikit-learn via an ‘‘Estimator’’ object (initialization of the model). That means that you first prepare the object with some parameters and later you apply the fit method (in most cases) to process the data. After that predictions can be made. The process in SciKit is always the same: import the model, initialize the model, train or fit the model and use the model to predict.

For instance, consider a linear regression as it is implemented on the linear model of scikit-learn.

Sometimes we need to preprocess the data, for example, normalizing the values or introducing some shifts. When doing that we use in scikit-learn a pipeline. A pipeline is a chain of transforms and estimators. In our case, we will scale the data before feeding the classifier.

from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler

Estimator parameters: All the parameters of an estimator can be set when it is instantiated, and have suitable default values:

model = make_pipeline(StandardScaler(with_mean=False), LinearRegression())

print (model)

Pipeline(steps=[('standardscaler', StandardScaler(with_mean=False)),
                ('linearregression', LinearRegression())])

Estimated Model parameters: When data is fit with an estimator, parameters are estimated from the data at hand. All the estimated parameters are attributes of the estimator object ending by an underscore:

For example consider as five points in the $x$ domain and the function $y=f(x)$ will include some small randomness

x = np.arange(10)
y = 0.9*np.arange(10)+ 1.5*(np.random.rand(10)-0.5)

Let’s plot those points with a quick plot

plt.plot(x, y, 'o')
plt.xlim(-0.5, np.max(x)+0.5)
plt.ylim(-0.5, np.max(y)+0.5);
plt.gca().set_aspect('equal')

png

scikit-learn needs the input data as a 2D array instead of a unidimensional array. The solution is to add a new axis to the original x array using numpy.newaxis

# The input data for sklearn is 2D: (samples == 3 x features == 1)
X = x[:, np.newaxis]
print (X)
print (y)

[[0]
 [1]
 [2]
 [3]
 [4]
 [5]
 [6]
 [7]
 [8]
 [9]]
[0.42997443 0.92424111 2.42936148 2.0983617  3.18032488 3.78568145
 5.20383986 6.90867634 7.93853267 8.12147514]

model.fit(X, y)

Pipeline(steps=[('standardscaler', StandardScaler(with_mean=False)),
                ('linearregression', LinearRegression())])

model['linearregression'].coef_

array([2.6223391])

model['linearregression'].intercept_

-0.006368893054832903

The model found a line with a slope $\approx 1.14$ and intercept $\approx 0.15$, slightly different from the slope $0.9$ and intercept $0.0$ if random numbers were not creating deviations in the data.

Classification (K nearest neighbors)

K nearest neighbors (kNN) is one of the simplest non-parametric learning strategies that can be used for classification.

kNN is one of the simpler algorithms that stores all available cases and predicts the numerical target based on a similarity measure (e.g., distance functions which are based on a metric definition, where the Euclidean, Manhattan, or Minkowski are the most used ones). An important detail to keep in mine is that all features should be measured on the same scale. In case the scale is not the same, the scale should be standarized.

The algorithm can be summarized as follows: given a new, unknown observation, look up in your reference database which ones have the closest features and assign the predominant class.

Let’s try it out on our iris classification problem:

from sklearn import neighbors, datasets

iris = datasets.load_iris()
X, y = iris.data, iris.target

# create the model
knn = neighbors.KNeighborsClassifier(n_neighbors=1)

# fit the model
knn.fit(X, y)

# What kind of iris has 3cm x 5cm sepal and 4cm x 2cm petal?
# call the "predict" method:
result = knn.predict([[3, 5, 4, 2],])

print (iris.target_names[result])

['virginica']

Using this kNN we can create a map of all the different outcomes fixing the values of 3cm x 5cm sepal. Here we will use the linspace function from NumPy that return evenly spaced numbers over a specified interval.

N=100
preds = np.zeros((N,N))
x0 = 3
x1 = 5
minx2=np.min(iris.data[:,2])
maxx2=np.max(iris.data[:,2])
x2 = np.linspace(minx2, maxx2, N, endpoint=True)
minx3=np.min(iris.data[:,3])
maxx3=np.max(iris.data[:,3])
x3 = np.linspace(minx3, maxx3, N, endpoint=True)

for i in range(N):
    for j in range(N):
        preds[i,j]=knn.predict([[x0, x1 , x2[i], x3[j]],])[0] # To prevent deprecation from new Numpy behavior

formatter = plt.FuncFormatter(lambda i, *args: iris.target_names[int(i)])

plt.imshow(preds[::-1], extent=[minx2,maxx2, minx3, maxx3],aspect='auto')
plt.colorbar(ticks=[0, 1, 2], format=formatter)
plt.xlabel(iris.feature_names[2])
plt.ylabel(iris.feature_names[3]);

png

Classification (Support Vector Machines)

The goal of the support vector machine (SVM) algorithm is to find a hyperplane in an N-dimensional space(where N is the number of features) that distinctly classifies the data points. This algorithm receives a given labeled training data (supervised learning), the algorithm outputs an optimal hyperplane which categorizes new examples. In two dimensional space this hyperplane is a line dividing a plane into two parts where each class lay on either side of the plane.

To separate the two classes of data points, there are many possible hyperplanes that could be chosen. Our objective is to find a plane that has the maximum margin, i.e the maximum distance between data points of both classes. Maximizing the margin distance provides some reinforcement so that future data points can be classified with more confidence.

from sklearn.svm import SVC

model = SVC(gamma='scale')
model.fit(X, y)
result = model.predict([[3, 5, 4, 2],])
print (iris.target_names[result])

['versicolor']

a=(5,)
a

(5,)

N=100
preds = np.zeros((N,N))
x0 = 3
x1 = 5
minx2=np.min(iris.data[:,2])
maxx2=np.max(iris.data[:,2])
x2 = np.linspace(minx2, maxx2, N, endpoint=True)
minx3=np.min(iris.data[:,3])
maxx3=np.max(iris.data[:,3])
x3 = np.linspace(minx3, maxx3, N, endpoint=True)

for i in range(N):
    for j in range(N):
        preds[i,j]=model.predict([[x0, x1 , x2[i], x3[j]],])[0] # The [0] prevents deprecation warnings on Numpy 1.25+

formatter = plt.FuncFormatter(lambda i, *args: iris.target_names[int(i)])

plt.imshow(preds[::-1], extent=[minx2,maxx2,minx3,maxx3],aspect='auto')
plt.colorbar(ticks=[0, 1, 2], format=formatter)
plt.xlabel(iris.feature_names[2])
plt.ylabel(iris.feature_names[3]);

png

Regression Example

Simplest possible regression is fitting a line to data:

# Create some simple data
np.random.seed(0)
X = np.random.random(size=(20, 1))
y = 3 * X.squeeze() + 2 + np.random.normal(size=20)

# Fit a linear regression to it
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=True)
model.fit(X, y)
print ("Model coefficient: %.5f, and intercept: %.5f"
       % (model.coef_, model.intercept_))

# Plot the data and the model prediction
X_test = np.linspace(0, 1, 100)[:, np.newaxis]
y_test = model.predict(X_test)

plt.plot(X.squeeze(), y, 'o')
plt.plot(X_test.squeeze(), y_test);

Model coefficient: 3.93491, and intercept: 1.46229

png

Classification (Perceptrons)

The perceptron is an algorithm for learning a binary classifier called a Linear classifier, a function that maps its input $\mathbf{x}$ (a real-valued vector) to an output value $f(\mathbf{x})$ (a single binary value):

[f(\mathbf{x}) = \begin{cases}1 & \text{if }\ \mathbf{w} \cdot \mathbf{x} + b > 0,\0 & \text{otherwise}\end{cases}]

where $\mathbf{w}$ is a vector of real-valued weights, $\mathbf{w} \cdot \mathbf{x}$ is the dot product

$\mathbf{w} \cdot \mathbf{x} = \sum_{i=1}^m w_i x_i$,

where $m$ is the number of inputs to the perceptron, and $b$ is the bias. The bias shifts the decision boundary away from the origin and does not depend on any input value.

The value of $f(\mathbf{x})$ (0 or 1) is used to classify $\mathbf{x}$ as either a positive or a negative instance, in the case of a binary classification problem. If is negative, then the weighted combination of inputs must produce a positive value greater than $

$ to push the classifier neuron over the 0 thresholds. Spatially, the bias alters the position (though not the orientation) of the [[decision boundary]]. The perceptron learning algorithm does not terminate if the learning set is not [[linearly separable]]. If the vectors are not linearly separable learning will never reach a point where all vectors are classified properly. The most famous example of the perceptron’s inability to solve problems with linearly nonseparable vectors is the Boolean [[exclusive-or]] problem.

In the context of neural networks, a perceptron is an artificial neuron using the Heaviside step function as the activation function. The perceptron algorithm is also termed the single-layer perceptron, to distinguish it from a multilayer perceptron, which is a misnomer for a more complicated neural network. As a linear classifier, the single-layer perceptron is the simplest feedforward neural network.

from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron

Let’s recreate the iris dataset and select two variables from it: petal length, petal width.

iris = load_iris()
X = iris.data[:, (2, 3)]  # petal length, petal width
y = (iris.target == 0).astype(np.int32)

axes = [0, 7, 0, 3]
plt.figure(figsize=(10, 4))
plt.plot(X[y==0, 0], X[y==0, 1], "bs", label="Not Iris-Setosa")
plt.plot(X[y==1, 0], X[y==1, 1], "yo", label="Iris-Setosa")

plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14);
plt.axis(axes);

png

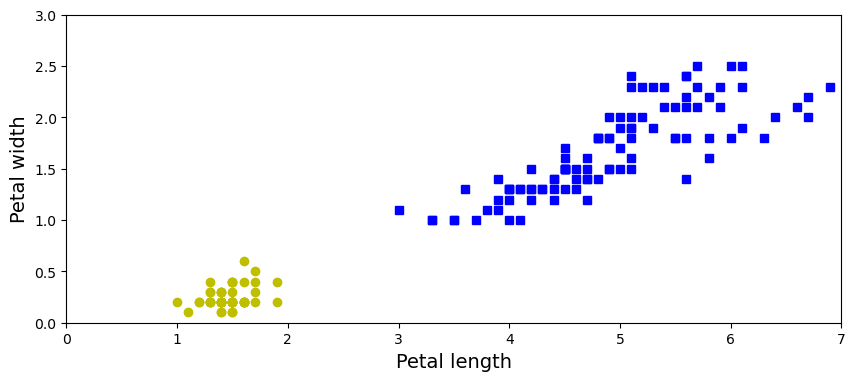
per_clf = Perceptron(max_iter=1000, tol=1e-3, random_state=42) # we set `max_iter` and `tol` explicitly to avoid
                                                               # warnings about the fact that their default value
                                                               # will change in future versions of Scikit-Learn.
per_clf.fit(X, y)

y_pred = per_clf.predict([[2, 0.5]])

y_pred

array([1], dtype=int32)

a = -per_clf.coef_[0][0] / per_clf.coef_[0][1]
b = -per_clf.intercept_ / per_clf.coef_[0][1]

axes = [0, 7, 0, 3]
plt.figure(figsize=(10, 4))
plt.plot(X[y==0, 0], X[y==0, 1], "bs", label="Not Iris-Setosa")
plt.plot(X[y==1, 0], X[y==1, 1], "yo", label="Iris-Setosa")

plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14);
plt.plot([axes[0], axes[1]], [a * axes[0] + b, a * axes[1] + b], "k-", linewidth=3)
plt.axis(axes);

png

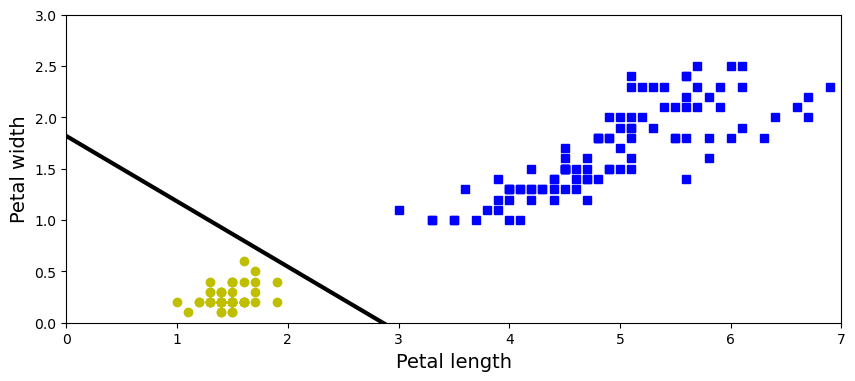
axes = [0, 7, 0, 3]

x0, x1 = np.meshgrid(
        np.linspace(axes[0], axes[1], 500).reshape(-1, 1),
        np.linspace(axes[2], axes[3], 200).reshape(-1, 1),
    )
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = per_clf.predict(X_new)
zz = y_predict.reshape(x0.shape)

plt.figure(figsize=(10, 4))
plt.plot(X[y==0, 0], X[y==0, 1], "bs", label="Not Iris-Setosa")
plt.plot(X[y==1, 0], X[y==1, 1], "yo", label="Iris-Setosa")

plt.plot([axes[0], axes[1]], [a * axes[0] + b, a * axes[1] + b], "k-", linewidth=3)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#9898ff', '#fafab0'])

plt.contourf(x0, x1, zz, cmap=custom_cmap)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="lower right", fontsize=14)
plt.axis(axes);

png

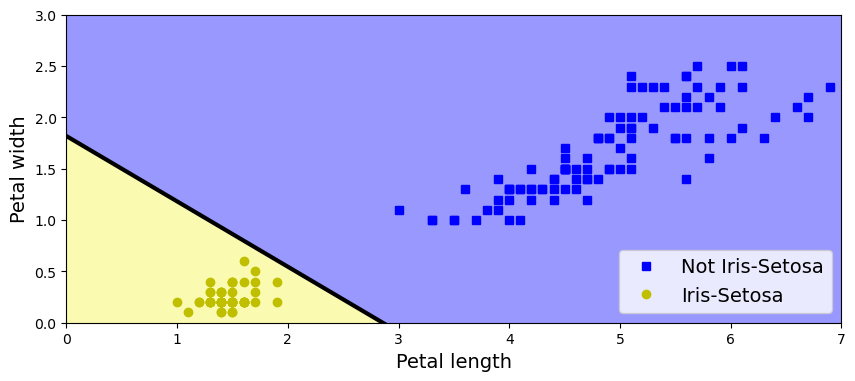
Dimensionality Reduction (PCA)

Unsupervised Learning addresses a different sort of problem. Here the data has no labels, and we are interested in finding a pattern or structure between the objects in question. In a sense, you can think of unsupervised learning as a means of discovering labels from the data itself. Unsupervised learning comprises tasks such as dimensionality reduction, clustering, and density estimation. For example, in the iris data discussed above, we can use unsupervised methods to determine combinations of the measurements which best display the structure of the data. As we’ll see below, such a projection of the data can be used to visualize the four-dimensional dataset in two dimensions. Some more involved unsupervised learning problems are:

given detailed observations of distant galaxies, determine which features or combinations of features best summarize the information.
given a mixture of two sound sources (for example, a person talking over some music), separate the two (this is called the blind source separation problem).
given a video, isolate a moving object and categorize it in relation to other moving objects which have been seen.
A given crystal structure, we can use to predict the stability.

Sometimes the two may even be combined: e.g. Unsupervised learning can be used to find useful features in heterogeneous data, and then these features can be used within a supervised framework.

Principal Component Analysis (PCA) is a dimension reduction technique that can find the combinations of variables that explain the most variance. This method is one of the most popular linear dimension reduction methodologies available in machine learning. Sometimes, it is used alone and sometimes as a starting solution for other dimension reduction methods. PCA is a projection-based method that transforms the data by projecting it onto a set of orthogonal axes.

Consider the iris dataset. It cannot be visualized in a single 2D plot, as it has 4 features. We are going to extract 2 combinations of sepal and petal dimensions to visualize it:

X, y = iris.data, iris.target
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X)
X_reduced = pca.transform(X)
print ("Reduced dataset shape:", X_reduced.shape)

fig,ax=plt.subplots(figsize=(8,6))

ax.scatter(X_reduced[:, 0], X_reduced[:, 1], c=y)

print ("Meaning of the 2 components:")
for component in pca.components_:
    print (" + ".join("%.3f x %s" % (value, name)
                     for value, name in zip(component,
                                            iris.feature_names)))

Reduced dataset shape: (150, 2)
Meaning of the 2 components:
0.361 x sepal length (cm) + -0.085 x sepal width (cm) + 0.857 x petal length (cm) + 0.358 x petal width (cm)
0.657 x sepal length (cm) + 0.730 x sepal width (cm) + -0.173 x petal length (cm) + -0.075 x petal width (cm)

png

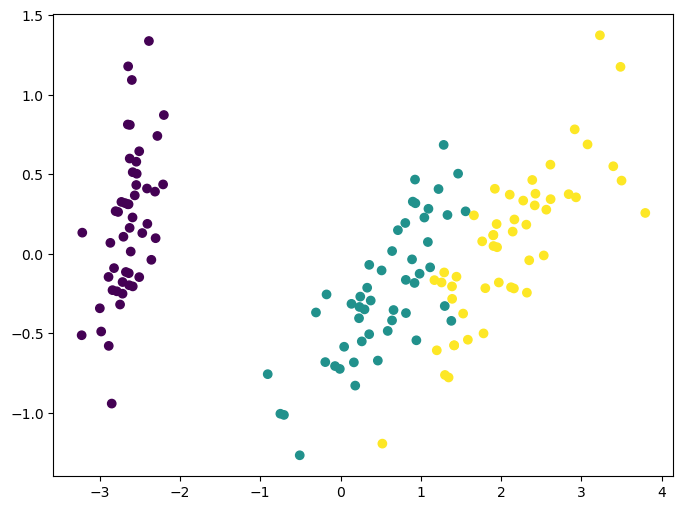
Clustering: K-means

K-means clustering is one of the simplest and most popular unsupervised machine learning algorithms by practicioners. As discussed before, unsupervised algorithms make inferences from datasets using only input vectors without referring to known, or labeled, outcomes. AndreyBu, who has more than 5 years of machine learning experience and currently teaches people his skills, says that “the objective of K-means is simple: group similar data points together and discover underlying patterns. To achieve this objective, K-means looks for a fixed number (k) of clusters in a dataset.”

The main idea with this algorithm is to group similar data into clusters and try to find the underlying developed pattern by looking at how the data clusters into a fixed number of (k) clusters in the dataset.

Note that these clusters will uncover relevant hidden structure of the data only if the criterion used highlights it.

from sklearn.cluster import KMeans
k_means = KMeans(n_clusters=3, random_state=0) # Fixing the RNG in kmeans
k_means.fit(X)
y_pred = k_means.predict(X)

fig,ax=plt.subplots(figsize=(8,6))

ax.scatter(X_reduced[:, 0], X_reduced[:, 1], c=y_pred);

png

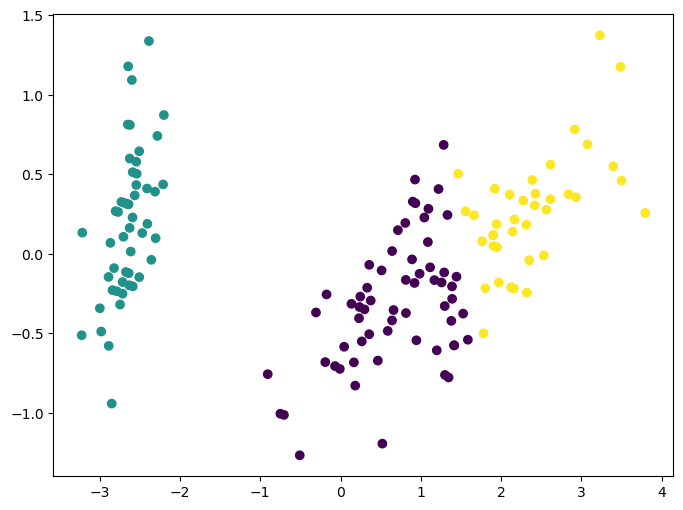
Scikit-learn’s estimator interface

Scikit-learn strives to have a uniform interface across all methods. Given a scikit-learn estimator object named model, the following methods are available:

Available in all Estimators
- model.fit() : fit training data. For supervised learning applications, This accepts two arguments: the data X and the labels y (e.g. model.fit(X, y)). For unsupervised learning applications, this accepts only a single argument, the data X (e.g. model.fit(X)).
Available in supervised estimators
- model.predict() : given a trained model, predict the label of a new set of data. This method accepts one argument, the new data X_new (e.g. model.predict(X_new)), and returns the learned label for each object in the array.
- model.predict_proba() : For classification problems, some estimators also provide This method, returns the probability that a new observation has each categorical label. In this case, the label with the highest probability is returned by model.predict().
- model.score() : for classification or regression problems, most (all?) estimators implement a score method. Scores are between 0 and 1, with a larger score indicating a better fit.
Available in unsupervised estimators
- model.transform() : given an unsupervised model, transform new data into the new basis. This also accepts one argument X_new, and returns the new representation of the data based on the unsupervised model.
- model.fit_transform() : some estimators implement this method, which more efficiently performs a fit and a transform on the same input data.

Other small datasets to explore

Scikit learn offers a collection of small datasets like iris for learning purposes. In addition to that, scikit also includes functions to download and prepare larger datasets. Finally, some datasets can be generated randomly under some models.

Small datasets

These small datasets are packaged with the scikit-learn installation, and can be downloaded using the tools in sklearn.datasets.load_*

[x for x in sklearn.datasets.__dict__.keys() if x[:5]=='load_']

['load_breast_cancer',
 'load_diabetes',
 'load_digits',
 'load_files',
 'load_iris',
 'load_linnerud',
 'load_sample_image',
 'load_sample_images',
 'load_wine',
 'load_svmlight_file',
 'load_svmlight_files']

Dataset fetcher

These larger datasets are available for download (BE CAREFUL WITH THE CONNECTION!), and scikit-learn includes tools that streamline this process. These tools can be found in sklearn.datasets.fetch_*

[x for x in sklearn.datasets.__dict__.keys() if x[:6]=='fetch_']

['fetch_california_housing',
 'fetch_covtype',
 'fetch_kddcup99',
 'fetch_lfw_pairs',
 'fetch_lfw_people',
 'fetch_olivetti_faces',
 'fetch_openml',
 'fetch_rcv1',
 'fetch_species_distributions',
 'fetch_20newsgroups',
 'fetch_20newsgroups_vectorized']

Modeled datasets

Finally, there are several datasets that are generated from models based on a random seed. These are available in the sklearn.datasets.make_*

[x for x in sklearn.datasets.__dict__.keys() if x[:5]=='make_']

['make_biclusters',
 'make_blobs',
 'make_checkerboard',
 'make_circles',
 'make_classification',
 'make_friedman1',
 'make_friedman2',
 'make_friedman3',
 'make_gaussian_quantiles',
 'make_hastie_10_2',
 'make_low_rank_matrix',
 'make_moons',
 'make_multilabel_classification',
 'make_regression',
 'make_s_curve',
 'make_sparse_coded_signal',
 'make_sparse_spd_matrix',
 'make_sparse_uncorrelated',
 'make_spd_matrix',
 'make_swiss_roll']

Handwritten Digits Data Set: Validation and Model Selection

This section focuses on validation and model selection.

The small 8x8 dataset

Features can be any uniformly measured numerical observation of the data. For example, in the digits data, the features are the brightness of each pixel:

digits = sklearn.datasets.load_digits()
digits.data.shape

(1797, 64)

print(digits.DESCR)

.. _digits_dataset:

Optical recognition of handwritten digits dataset
--------------------------------------------------

**Data Set Characteristics:**

    :Number of Instances: 1797
    :Number of Attributes: 64
    :Attribute Information: 8x8 image of integer pixels in the range 0..16.
    :Missing Attribute Values: None
    :Creator: E. Alpaydin (alpaydin '@' boun.edu.tr)
    :Date: July; 1998

This is a copy of the test set of the UCI ML hand-written digits datasets
https://archive.ics.uci.edu/ml/datasets/Optical+Recognition+of+Handwritten+Digits

The data set contains images of hand-written digits: 10 classes where
each class refers to a digit.

Preprocessing programs made available by NIST were used to extract
normalized bitmaps of handwritten digits from a preprinted form. From a
total of 43 people, 30 contributed to the training set and different 13
to the test set. 32x32 bitmaps are divided into nonoverlapping blocks of
4x4 and the number of on pixels are counted in each block. This generates
an input matrix of 8x8 where each element is an integer in the range
0..16. This reduces dimensionality and gives invariance to small
distortions.

For info on NIST preprocessing routines, see M. D. Garris, J. L. Blue, G.
T. Candela, D. L. Dimmick, J. Geist, P. J. Grother, S. A. Janet, and C.
L. Wilson, NIST Form-Based Handprint Recognition System, NISTIR 5469,
1994.

.. topic:: References

  - C. Kaynak (1995) Methods of Combining Multiple Classifiers and Their
    Applications to Handwritten Digit Recognition, MSc Thesis, Institute of
    Graduate Studies in Science and Engineering, Bogazici University.
  - E. Alpaydin, C. Kaynak (1998) Cascading Classifiers, Kybernetika.
  - Ken Tang and Ponnuthurai N. Suganthan and Xi Yao and A. Kai Qin.
    Linear dimensionalityreduction using relevance weighted LDA. School of
    Electrical and Electronic Engineering Nanyang Technological University.
    2005.
  - Claudio Gentile. A New Approximate Maximal Margin Classification
    Algorithm. NIPS. 2000.

digits.target_names

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

N=3
M=6
fig, axs = plt.subplots(N,M,sharex=True, sharey=True, figsize=(12,6))
for i in range(N):
    for j in range(M):
        axs[i,j].imshow(digits['images'][N*j+i], cmap='gray')

png

Gaussian Naive Bayes Estimator

Let’s show a quick classification example, using the simple-and-fast Gaussian Naive Bayes estimator. Naive Bayes methods are a set of supervised learning algorithms based on applying Bayes’ theorem with the “naive” assumption of conditional independence between every pair of features given the value of the class variable. Bayes’ Theorem provides a mathematical procedure where we can calculate the probability of a hypothesis given our prior knowledge. This can be described by this equation

$P[h|d] = \frac{P[d|h] P[h]}{P[d]}$ where $P$ is a probability distribution function, $d$ is the historic data and $h$ is the tested hypothesis. Therefore, this equation can be read as follows: the conditional probability (posterior) of a given hypothesis occurs provided the data $d$ can be obtained as the fraction between the product of the probability that the data $d$ occurs given that $h$ is true with the probability of the hypothesis divided by the probability of the data.

Now, the posterior probability can be obtained from several different hypotheses. Based on this, the maximum probable hypothesis (MAP: maximum probably hypothesis) can be calculated and
After calculating the posterior probability for several different hypotheses, you can select the hypothesis with the highest probability. This is the maximum probable hypothesis and may formally be called the maximum a posteriori (MAP) hypothesis. How we account for the different probability terms gives rise to different methods.

In the so-called naive Bayes, the probabilities for each hypothesis are simplified, such that the calculation becomes easier. This approximation will say that the data realization to obtain $P[d	h]$ is independent, which means that
$P[d	h] = P[d_1	h] P[d_2	h] P[d_3	h] \cdots$.

Now, the method reduces to the following. By entering a set of classified data (training), we can use it to obtain the probabilities of each class and the conditional probabilities of each input value given to each class. This last probability is obtained directly from the training data as the frequency of each feature in a given class is divided by the frequency of instances of that class value.

A very simple case is observed as follows:

from sklearn.naive_bayes import GaussianNB
X = digits.data
y = digits.target

# Instantiate the estimator
clf = GaussianNB()

# Fit the estimator to the data, leaving out the last five samples
clf.fit(X[:-5], y[:-5])

# Use the model to predict the last several labels
y_pred = clf.predict(X[-5:])

print (y_pred)
print (y[-5:])

[9 0 8 9 8]
[9 0 8 9 8]

We see that this relatively simple model leads to a perfect classification of the last few digits!

Let’s use the model to predict labels for the full dataset, and plot the confusion matrix, which is a convenient visual representation of how well the classifier performs.

By definition a confusion matrix $C$ is such that $C_{i, j}$ is equal to the number of observations known to be in $i$ but predicted to be in the group $j$

from sklearn import metrics

clf = GaussianNB()
clf.fit(X, y)
y_pred = clf.predict(X)

def plot_confusion_matrix(y_pred, y):
    plt.imshow(metrics.confusion_matrix(y, y_pred),
               cmap=plt.cm.binary, interpolation='none')
    plt.colorbar()
    plt.xlabel('true value')
    plt.ylabel('predicted value')

print ("classification accuracy:", metrics.accuracy_score(y, y_pred))
plot_confusion_matrix(y, y_pred)

classification accuracy: 0.8580968280467446

png

Interestingly, there is confusion between some values. In particular, the number 2 is often mistaken for the number 8 by this model! But for the vast majority of digits, we can see that the classification looks correct.

Let’s use the metrics submodule again to print the accuracy of the classification:

print (metrics.accuracy_score(y, y_pred))

0.8580968280467446

We have an 82% accuracy rate with this particular model.

But there’s a problem: we are testing the model on the data we used to train the model. As we’ll see later, this is generally not a good approach to model validation! Because of the nature of the Naive Bayes estimator, it’s alright in this case, but we’ll see later examples where this approach causes problems.

Model Validation

An important piece of the learning task is the measurement of prediction performance, also known as model validation. We’ll go into detail about this, but first, motivate the approach with an example.

The Importance of Splitting

Above we looked at a confusion matrix, which can be computed based on the results of any model. Let’s look at another classification scheme here, the K-Neighbors Classifier

from sklearn.neighbors import KNeighborsClassifier
from sklearn import datasets

digits = datasets.load_digits()
X, y = digits.data, digits.target

clf = KNeighborsClassifier(n_neighbors=1)
clf.fit(X, y)
y_pred = clf.predict(X)

print ("classification accuracy:", metrics.accuracy_score(y, y_pred))
plot_confusion_matrix(y, y_pred)

classification accuracy: 1.0

png

Our classifier gives perfect results! Have we settled on a perfect classification scheme?

No! The K-neighbors classifier is an example of an instance-based classifier, which memorizes the input data and compares any unknown sample to it. To accurately measure the performance, we need to use a separate validation set, which the model has not yet seen.

Scikit-learn contains utilities to split data into a training and validation set:

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
print (X_train.shape, X_test.shape)

(1257, 64) (540, 64)

clf = KNeighborsClassifier(n_neighbors=1)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)

print ("classification accuracy:", metrics.accuracy_score(y_test, y_pred))
plot_confusion_matrix(y_test, y_pred)

classification accuracy: 0.9833333333333333

png

This gives us a more accurate indication of how well the model is performing.

For this reason, you should always do a train/test split when validating a model.

Exploring Validation Metrics

Above, we used perhaps the most simple evaluation metric, the number of matches and mismatches. But this is not always sufficient. For example, imagine you have a situation where you’d like to identify a rare class of event from within a large number of background sources.

# Generate an un-balanced 2D dataset
np.random.seed(0)
X = np.vstack([np.random.normal(0, 1, (950, 2)),
               np.random.normal(-1.8, 0.8, (50, 2))])
y = np.hstack([np.zeros(950), np.ones(50)])

plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='none',
            cmap=plt.cm.Accent);

png

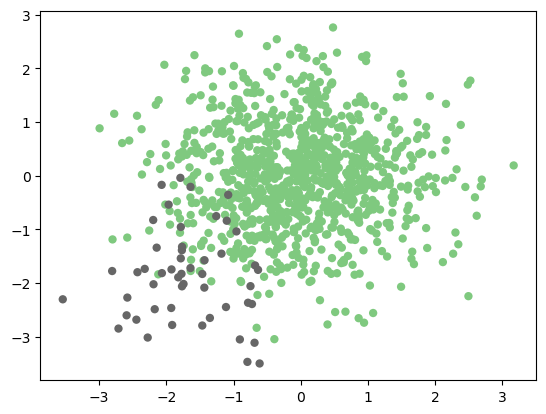
Exploring other Validation Scores

Until now we are using only the accuracy to evaluate our algorithms. We can calculate other scores such as the precision, the recall, and the f1 score:

from sklearn import metrics
from sklearn.svm import SVC

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
clf = SVC(kernel='linear').fit(X_train, y_train)
y_pred = clf.predict(X_test)

print ("accuracy:", metrics.accuracy_score(y_test, y_pred))
print ("precision:", metrics.precision_score(y_test, y_pred))
print ("recall:", metrics.recall_score(y_test, y_pred))
print ("f1 score:", metrics.f1_score(y_test, y_pred))

accuracy: 0.972
precision: 0.8
recall: 0.75
f1 score: 0.7741935483870969

What do these mean?

These are ways of taking into account not just the classification results, but the results relative to the true category.

[{\rm accuracy} \equiv \frac{\rm correct~labels}{\rm total~samples}]

[{\rm precision} \equiv \frac{\rm true~positives}{\rm true~positives + false~positives}]

[{\rm recall} \equiv \frac{\rm true~positives}{\rm true~positives + false~negatives}]

[F_1 \equiv 2 \frac{\rm precision \cdot recall}{\rm precision + recall}]

The accuracy, precision, recall, and f1-score all range from 0 to 1, with 1 being optimal. Here we’ve used the following definitions:

True Positives are those which are labeled 1 which are actually 1
False Positives are those which are labeled 1 which are actually 0
True Negatives are those which are labeled 0 which are actually 0
False Negatives are those which are labeled 0 which are actually 1

We can quickly compute a summary of these statistics using scikit-learn’s provided convenience function:

print (metrics.classification_report(y_test, y_pred,
                                    target_names=['background', 'foreground']))

              precision    recall  f1-score   support

  background       0.98      0.99      0.99       234
  foreground       0.80      0.75      0.77        16

    accuracy                           0.97       250
   macro avg       0.89      0.87      0.88       250
weighted avg       0.97      0.97      0.97       250

This tells us that, though the overall correct classification rate is 97%, we only correctly identify 67% of the desired samples, and those that we label as positives are only 83% correct! This is why you should make sure to carefully choose your metric when validating a model.

Cross-Validation

Using the simple train/test split as above can be useful, but there is a disadvantage: You’re ignoring a portion of your dataset. One way to address this is to use cross-validation.

The simplest cross-validation scheme involves running two trials, where you split the data into two parts, first training on one, then training on the other:

X1, X2, y1, y2 = train_test_split(X, y, test_size=0.5)
print (X1.shape)
print (X2.shape)

(500, 2)
(500, 2)

y2_pred = SVC(kernel='linear').fit(X1, y1).predict(X2)
y1_pred = SVC(kernel='linear').fit(X2, y2).predict(X1)

print (np.mean([metrics.precision_score(y1, y1_pred),
               metrics.precision_score(y2, y2_pred)]))

0.7467320261437909

This is known as two-fold cross-validation, and is a special case of K-fold cross validation.

Because it’s such a common routine, scikit-learn has a K-fold cross-validation scheme built-in:

from sklearn.model_selection import cross_val_score

# Let's do a 2-fold cross-validation of the SVC estimator
print (cross_val_score(SVC(kernel='linear'), X, y, cv=2, scoring='precision'))

[0.75       0.84210526]

It’s also possible to use sklearn.cross_validation.KFold and sklearn.cross_validation.StratifiedKFold directly, as well as other cross-validation models which you can find in the cross_validation module.

Example: The SVC classifier takes a parameter C whose default value is 1. Using 5-fold cross-validation, make a plot of the precision as a function of C, for the SVC estimator on this dataset. For best results, use a logarithmic spacing of C between 0.1 and 100.

Cs = np.logspace(-1.5, 2, 10)
scores = []

for C in Cs:
    score = cross_val_score(SVC(kernel='linear', C=C), X, y, cv=5, scoring='precision')
    scores.append(score.mean())

plt.semilogx(Cs, scores, 'o-');

png

Grid Search

The previous exercise is an example of a grid search for model evaluation. Again, because this is such a common task, Scikit-learn has a grid search tool built-in, which is used as follows. Note that GridSearchCV has a fit method: it is a meta-estimator: an estimator over estimators!

from sklearn.model_selection import GridSearchCV

clf = SVC(kernel='linear')
Crange = np.logspace(-1.5, 2, 10)

grid = GridSearchCV(clf, param_grid={'C': Crange},
                    scoring='precision', cv=5)
grid.fit(X, y)

print ("best parameter choice:", grid.best_params_)

best parameter choice: {'C': 0.03162277660168379}

scores = [g for g in grid.cv_results_['mean_test_score']]
plt.semilogx(Crange, scores, 'o-');

png

Grid search can come in very handy when you’re tuning a model for a particular task.

Acknowledgments

We acknowledge the support of the National Science Foundation and the US Department of Energy under projects: DMREF-NSF 1434897, NSF OAC-1740111 and DOE DE-SC0016176 is recognized.

References

The order of the books goes from divulgation and practical to the more rigorous and mathematical. Slides, blogs, and videos are those I have found over the internet or suggested by others.

Selection of Books on Machine Learning

Hands-On Machine Learning with Scikit-Learn and TensorFlow (First Edition [There is a second edition])
Auréleien Géron
2017

Machine Learning, a Probabilistic Perspective
Sebastian Raschka and Vahid Mirjalili
2017

Foundations of Machine Learning (Second Edition)
Mehryar Mohri, Afshin Rostamizadeh and Ameet Talwalkar
2018

Introduction to Machine Learning (Fourth Edition)
Ethem Alpaydin
2020

Machine Learning, a Probabilistic Perspective
Kevin P. Murphy
2012

Elements of Statistical Learning
Trevor Hastie, Robert Tibshirani, and Jerome Friedman
2008

Jupyter Notebooks

Yale Digital Humanities Lab
Aurelien Geron Hands-on Machine Learning with Scikit-learn First Edition and Second Edition
A progressive collection notebooks of the Machine Learning course by the University of Turin
A curated set of jupyter notebooks about many topics

Videos

Hands-On Machine Learning with Scikit-Learn and TensorFlow (OREILLY)

Machine Learning Cheatsheets

Mining of Massive Datasets

Convolutional Neural Networks for Visual Recognition

Machine Learning (Andrew Ng, Coursera)

Back of the Book

plt.figure(figsize=(3,3))
n = chapter_number
maxt=(2*(n-1)+3)*np.pi/2
t = np.linspace(np.pi/2, maxt, 1000)
tt= 1.0/(t+0.01)
x = (maxt-t)*np.cos(t)**3
y = t*np.sqrt(np.abs(np.cos(t))) + np.sin(0.3*t)*np.cos(2*t)
plt.plot(x, y, c="green")
plt.axis('off');

png

end = time.time()
print(f'Chapter {chapter_number} run in {int(end - start):d} seconds')

Chapter 2 run in 26 seconds

Key Points

tmux allows you to keep terminal sessions on the cluster that persist in case of network disconnection.

Final remarks

Overview

Teaching: min
Exercises: min

Topics

Objectives

Use the break layout for placeholder episodes representing coffee breaks and lunches. These episodes do not have exercises, questions, objectives, or key points in their metadata, but must have a “break” field to show how long the break is (in minutes).

Key Points

Computational Partial Differential Equations

Overview

Teaching: 90 min
Exercises: 30 min

Topics

Day 2: General Relativity and GRMHD

Objectives

Day 2: General Relativity and GRMHD

Computational Partial Differential Equations

Irene S. Nelson, PhD

Day 2: General Relativity and GRMHD

General Relativity Primer

In the early 20th century, physics had a problem. Physicists had hypothesized that light must propagate through some medium known as the aether. However, when Michelson and Morley set out to try and detect this aether by measuring small differences in the speed of light at different points in the Earth’s orbit around the sun. However, much to their surprise, they found that, no matter what, the speed of light remained constant. Albert Einstein followed this startling realization to its logical conclusion: if the speed of light in a vacuum is always constant, then the flow of time and distances between fixed points cannot be constant. Instead, they depend on the speed of the observer. Ultimately, this led to the development of Einstein’s special theory of relativity.

Seeking to incorporate gravity into his theory of relativity, he noted that an observer in a box would be unable to tell whether the box was in a gravitational field or constantly accelerating. This insight, combined with special relativity, showed Einstein that the deeper into a gravitational field an observer is, the slower time passes for them. This eventually led Einstein to the general theory of relativity as we know it today.

In general relativity, space and time are combined into a single concept called spacetime, which is often visualized as a four-dimensional fabric that can stretch and deform in response the distribution of mass and energy in the spacetime. In turn, this distorted spacetime affects the paths of objects moving within it. That is, matter tells spacetime how to bend, and spacetime tells matter how to move. The standard demonstration for this concept imagines spacetime as a stretched rubber sheet. When a bowling ball is placed on the sheet, it bends the sheet, pulling it downwards. Then, when we try to roll a smaller ball on the sheet in a straight line, we find that the ball’s path is bent around the bowling ball. In much the same way, when an asteroid approaches near the Earth, we see its orbit bent around our planet. Less obviously, we can even see light rays bend around the sun, as was first observed by Dyson and Eddington in 1919.

Since then, Einstein’s theory has been experimentally verified over and over again. Of course, in order to experimentally verify a theory, we must first make predictions with that theory. In GR, these predictions are made by finding solutions to the Einstein equations. Unfortunately, this is easier said than done. There are very few known exact solutions to this set of equations, and as mentioned previously, these solutions do not correspond to physically-likely scenarios. As such, we often use approximate computational solutions instead.

A Note on Units

The standard convention in GR is to use what we call “geometrized units”. In this system, define the speed of light $c$ and universal gravitational constant $G$ to both be exactly one. Doing so allows us most quantities of interest (including masses and times) in units of length. When we do this, we find that one second is $2.998 \times 10^8$ meters and one kilogram is $7.426 \times 10^{-28}$ meters.

This will also allow us to express many quantities as multiples of black hole mass. For example, in a simulation, the mass of a black hole is simple called $M$. The masses of other black holes can then be defined defined as a multiple of the first black holes mass, like $2M$ or $M/2$. We can also express the distance between two black holes as a multiple of their mass, e.g. $50M$. The effects we observe are scale invariant: no matter what the value of $M$ is, if we place two black holes with that mass $50M$ apart, we will observe the same effects, whether they are two millimeter-mass black holes 50 mm apart or two kilometer-mass black holes 50 km apart.

Black Hole Simulations

General relativity, and, in particular, the interactions between space, time, gravity, and mass and energy, are described by the Einstein field equations. These equations show us how the distribution of matter and energy in the universe are related to the metric tensor, $g_{\mu \nu}$. The metric tensor describes how spacetime is curved in by detailing how to calculate the distance between different points in space and time.

To determine how any system behaves in general relativity, we must find a solution to the Einstein field equations. Unfortunately, there are very few exact solutions, and the exact solutions that are known are limited to scenarios such as a gravitational wave propagating through empty space or a single black hole. More complicated systems will require us to numerically integrate the equations to find an approximate solution.

To do so, we will use a very powerful code package called the Einstein Toolkit (ETK), which is part of the Cactus Computational Toolkit (CCTK). The CCTK is made up of individual modules known as “thorns” which provide the functionality we need. There are thorns for setting up the numerical grid, for solving for initial data, applying boundary conditions, and so on. Cactus provides a common interface to allow all these thorns to interact with each other and share data.

Below are links to some example simulations for the Toolkit.

https://einsteintoolkit.org/gallery.html

https://einsteintoolkit.org/gallery/bbh/index.html

However, we cannot apply the usual techniques of numerical integration just yet. As discussed previously, those techniques assume that we have a grid of points on space, and that the locations of those points stay constant, and that time flows uniformly everywhere in our computational domain. But as we just mentioned, this is not the case in general relativity. So, we must break up the rank-four metric tensor $g_{\mu \nu}$, slicing up spacetime into layers. When we do so, we get the rank-three metric tensor $\gamma_{i j}$, which describes the curvature of spacetime in a single layer, the shift vector $\beta_{i}$, which describes how a grid cell’s position will change in between slices, and the lapse $\alpha$, which describes how much time will pass at a point in between slices.

There are infinitely many ways we can choose to define our coordinate system in this way. Thus, we must be very careful about how we talk about the numbers that we will pass into our code; not all the parameters we set will have a readily interpretable physical meaning. In general, it is best to focus in invariant quantities like the dimensionless spin parameter. Two observers might not even agree whether two events are simultaneous in general relativity, but they will always agree on the spin of a black hole.

The 3+1 Decomposition:

Rinne, Oliver. (2014). Numerical and analytical methods for asymptotically flat spacetimes.

from IPython.display import Image
from IPython.core.display import HTML 
Path = "shooting_blackholes/"

Image(Path + "3-1-decomposition-with-unit-timelike-normal-n-a-lapse-function-a-and-shift-vector-b-i.png")

png

Induced Black Hole Spin

On Earth, coastal areas experience a tidal cycle twice per day. In many areas, the timing of these tides indicates a clear connection between the tides and the moon: high tide occurs both when the moon is directly overhead, and then again, about twelve hours later, when the moon is directly over the other side of the world.

Classical gravity offers a clear insight into why these things are connected. The gravitational force between any two objects depends on the mass of those objects and the distance between them. Because the gravity from one object pulls on all other objects, the moon is pulling on the planet as well as the oceans. However, the force of this pull decreases quickly the farther you get from the moon. Thus, the part of the ocean directly underneath it (i.e. closest to it) is experiences a stronger pull than Earth does, and the part of the ocean on the other side of the planet experiences a weaker pull. This causes the two tidal bulges to form in Earth’s oceans, giving us the familiar cycle of tides.

But the Earth is also spinning. As the Earth rotates, it pulls the tidal bulges along with it, so the tidal bulges aren’t directly in line with the moon. The moon’s gravity pulls back on them, however. Since the tidal bulges are no longer on the line between the centers of the Earth and moon, the moon exerts a torque on the planet, decreasing its angular momentum. In effect, the moon pulling on the Earth’s tides results in the day on Earth constantly getting a little bit longer.

This doesn’t just apply to the things on the Earth, though. It applies to the Earth itself, as well. This difference in force subtly stretches out the Earth. This effect can also be seen elsewhere in the Solar System, often to much more dramatic effect. Consider the moons of Jupiter. On Io, this constant stretching creates friction within the moon that heats it up, resulting in extreme volcanic activity. The images of the surface of Io taken by the Voyager probes are no longer accurate because the surface is being remodeled all the time. On Europa, this process creates enough heat to maintain a liquid ocean underneath miles of ice.

This leads us to an interesting question. If physical bodies can have their angular momentum changed by tidal effects, can the same thing happen to a black hole? At first, we might think that the answer is no, since all the mass in a black hole is concentrated at a single point called the singularity, and tides involve the gravitational force acting with different strengths at different distances.

However, that is only true in classical mechanics. In general relativity, gravity is a deformation in the fabric of spacetime. When one black hole deforms spacetime around it, it can distort nearby features in spacetime. In fact, when two black holes get close to merging, we can see that their event horizons are distorted by each other, eventually forming a two-lobed structure in the first instant after they merge. So perhaps “black hole tides” are not as unlikely a concept as we first thought?

Terrestrial Tides

https://commons.wikimedia.org/wiki/File:Tide_overview.svg

Image(Path + "Tide_overview.svg.png")

png

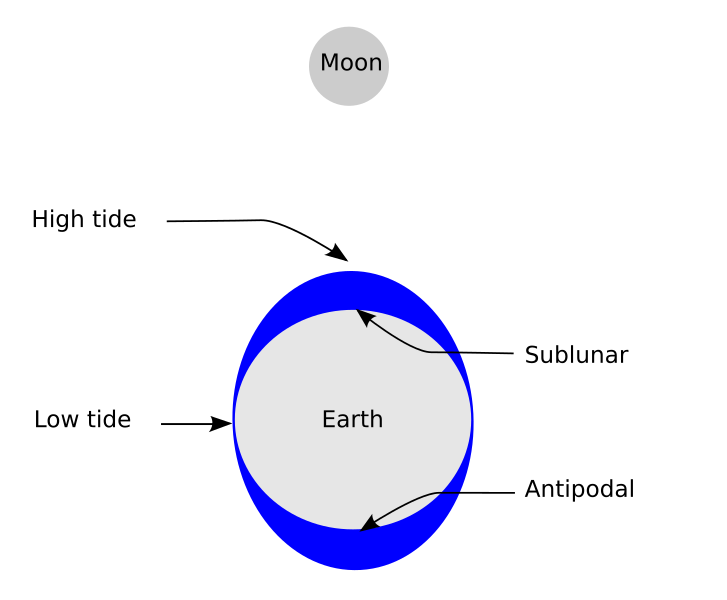
Example: Induced Black Hole Spin

To answer this question, we will set up a simple experiment. We will start with two equal mass, non-spinning black holes. (This sets up the simplest case with which we could answer this question.) We will also give them some initial momentum, shooting them towards each other. Our goal is to set the black holes on scattering trajectories: we want the black holes to interact in the strong-field regime, where the relativistic gravitational fields are strongest, but we also want to be careful not to let them merge.

So, the input parameters that are controlling will be the initial separation of the black holes, their initial speed, and the angle at which we shoot them.

Image(Path + "InitialDataSchematic.jpg")

jpeg

We will choose to set the initial separation of the black holes to $100 M$. It is important to start with the black holes quite far apart. This is because of a peculiarity with how we calculate the initial data. When the toolkit generates our initial data, it will set up two moving black holes and add their metrics together over a background of flat spacetime. However, in reality, the spacetime metric for this scenario would include contributions from their movement from infinite time beforehand.

Fortunately, the evolution equations are programmed in such a way that these inconsistencies will soon be resolved as the simulation advances. However, this also creates unphysical “junk” gravitational waves that propagate outwards (even exceeding the speed of light!); this is part of why it is vitally important to make sure that our boundary conditions are set up correctly. Our simulation’s outer boundary must allow the junk radiation to leave our computational domain, or else it could reflect back and interfere with the simulation.

Thus, while the junk radiation is ultimately inconsequential if we do everything correctly, it is still important to make sure the simulation has time to stabilize before the black holes strongly interact.

We will also set a coordinate velocity of $0.98$. (Ultimately, this number does not represent something observable). We will also choose an angle $\theta = 0.0550$.

Exploring the included parameter file


Thorns of Note:
- ADMBase, ML_BSSN: Solves the Einstein Equations
- AHFinderDirect: Calculates information about the apparent horizons
- Carpet: manages the coordinate grid
    - CarpetIOASCII: Outputs selected quantities
    - CarpetIOScalar: More outputs
- CoordBase: Sets the extent and resolution of the coarsest grid
- CarpetRegrid2: Controls the refinement levels
- MoL: the numerical integrator itself!
- PunctureTracker: Sets the initial position of the black holes and tracks their position
- QuasiLocalMeasures: Calculates the mass and spin of the black holes
- TwoPunctures: Our initial data of choice
- weylscal4: calculates gravitational wave data

#### Adaptive Mesh Refinement
Janiuk, Agnieszka & Charzyński, Szymon. (2016). Simulations of coalescing black holes. 


```python
Image(Path + "Adaptive-mesh-refinement-in-the-simulation-of-merging-black-holes.png")

png

After submitting this parameter file with the included job submission script, we are left with numerous text files.

We will focus on two in particular:

BH_diagnostics.ah1.gp contains information about the apparent horizons of the black holes
qlm_spin[0].norm2.asc has information about the spin of the black holes.

Also of note are the files mp_psi4_*.asc which contain the data we would need to use to analyse any gravitational waves emitted by this system.

We will start by analysing the trajectory of our black holes.

import matplotlib.pyplot as plt
import numpy as np

Path = "shooting_blackholes/ABE../fig/output_directory-Shooting_BlackHoles_using_TwoPunctures_theta_5.5000e-02__vel_9.8000e-01__sepRadius_5.0000e+01.par-mr/"
diagnostics1 = np.loadtxt(Path + "BH_diagnostics.ah1.gp")
diagnostics2 = np.loadtxt(Path + "BH_diagnostics.ah2.gp")
plt.figure()
plt.plot(diagnostics1[:,2],diagnostics1[:,3])
plt.plot(diagnostics2[:,2],diagnostics2[:,3])
plt.axis([-50, 50, -50, 50])
# plt.axis([-10, 10, -10, 10])
plt.gca().set_aspect('equal', adjustable='box')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

png

We will also take a look at the spin data; the time series clearly shows that we do in fact induce a final spin of about $0.03$.

spin = np.loadtxt(Path + "qlm_spin[0].norm2.asc")
plt.figure()
plt.plot(spin[:,1],spin[:,2])
plt.xlabel('time')
plt.ylabel('spin')
plt.show()

png

Array Jobs: Carrying Out a Study

But this is not the end of the story. In answering our first question, we have found many more. We will discuss two in particular:

Does the induced spin change as the black holes interact deeper in the strong field regime (i.e. as we decrease the shooting angle)?
Does the induced spin change as we impart a different initial velocity to the black holes?

To answer the first question we might set up an array job to try many different shooting angles $\theta$ at the same time. When we do so, we will discover that as we decrease the shooting angle, the final induced spin increases. So, to try to find the highest spin, we will want to try and find the angle that gets us as close to a merger as possible while still allowing the final black holes to escape to a greater distance.

This is an ideal case to create an array job.

angles0 = np.arange(0.054,0.066,0.001)
step0 = np.zeros_like(angles0)

angles1 = np.arange(0.054,0.058,0.0002)
step1 = np.zeros_like(angles1)+1

angles2 = np.arange(0.054,0.056,0.0001)
step2 = np.zeros_like(angles2)+2

plt.figure()
plt.plot(step0,angles0,'.')
plt.plot(step1,angles1,'.')
plt.plot(step2,angles2,'.')
plt.plot([0,1,2],[0.0545,0.0545,0.0545],'o')
plt.ylabel("theta")
plt.show()

png

When we want to explore how the induced spin changes with different initial velocities, we will repeat this procedure with a different initial boost.

Challenge: Find a Higher Final Spin

The highest spin that has been found with this setup is $0.20$, which is one-fifth of the maximum spin. However, it is very likely that it is possible to achieve a much higher spin. If you want to try to find a higher spin yourself, you will need to use a $v_0 > 1.5$. At your chosen initial speed, vary the angle to find the smallest $\theta$ that does not result in a merger. You will need to change the following parameters at the bottom of the parameter file.

TwoPunctures::par_P_plus[0]
TwoPunctures::par_P_minus[0]
TwoPunctures::par_P_plus[1]
TwoPunctures::par_P_minus[1]

The above parameters should be set to $\pm \frac{v_0}{2} \cos \theta$ $\pm \frac{v_0}{2} \sin \theta$ in accordance with the initial data schematic above.

Verifying Results

The fanciest simulation you can create is meaningless unless you can show that your results do, in fact, approximate reality, no matter how much memory or how many CPU hours you use. The codes that we have been using have been robustly tested to show that they can produce the expected results.

We will explore one method to do so using an exact solution from general relativistic force-free electrodynamics.

Stellar Remnants

We have already discussed one type of dead star, the black hole; we will briefly touch on the others.

Throughout a star’s life, the inward pull of gravity is balance by the outward pressure from the fusion reactions taking place in its core. However, as a star ages, it begins to run out of hydrogen to fuse in its core and must start fusing heavier and heavier elements together. Eventually, the star will reach a point where the pressure at its core is insufficient to continue the fusion process, and the star dies. The crushing inward pressure from gravity wins, and the star collapses. The final state depends on the star’s mass.

The least massive stars will shed their outer layers, forming a planetary nebula with a white dwarf at its center. More massive stars will explode violently in a supernova; the dense core left behind is more massive, and collapses into a denser neutron star. However, for the most massive stars, the dense remnant left behind becomes so dense that nothing can stop its complete collapse into a black hole.

General Relativistic Magnetohydrodynamics

When we want to study conducting fluids, we must combine Maxwell’s equations of electromagnetism with the equations of fluid dynamics; this field is known as Magnetohydrodynamics (MHD). These equations describe systems like stars, magnetospheres, and the interstellar medium. However, we must take things a step farther if the conducting fluid we want to study involves either extremely fast speeds or extremely dense objects.

In such a case, we must also incorporate the Einstein field equations; the resulting system is called general relativistic magnetohydrodynamics. These equations describe some of the most extreme events in the known universe such as neutron star mergers. Simulations of such events were crucial to deciphering the signals detected on 17 August 2017, when we detected the first neutron star merger simultaneously in gravitational and electromagnetic waves (GW170817 and GRB 170817A), ushering in the era of multi-messenger astrophysics.

We will consider an example from a special case of GRMHD, general relativistics force-free electrodynamics.

General Relativistic Force-Free Electrodynamics

General relativistics force-free electrodynamics (GRFFE) is a special case of GRMHD in which the magnetic pressure dominates the gas pressure. Such systems occur in systems with intense gravitational and magnetic fields. Neutron star magnetospheres are an example of a system that can be well-approximated by GRFFE.

Example: GRFFE Exact Wald

In order to explore one method of verifying that our code works as it should, we will examine the Exact Wald solution to the GRFFE equations. This solutions describes a single spinning black hole in a uniform magnetic field. A similar situation could occur in nature in a black hole-neutron star binary.

For our purposes, the most important thing about this solution is that it is time-independent; if our code were to work perfectly, as the simulation advances, everything should stay exactly the same.

This simulation will use:

ShiftedKerrSchild: initial data for a single spinning black hole
GiRaFFE: GRFFE solver
GiRaFFEfood: GRFFE initial data

Bz = np.loadtxt("Exact_Wald/GiRaFFE_tests_ExactWald/Bz.maximum.asc")
Bz_exact = Bz[0,2]

plt.figure()
plt.plot(Bz[1:,1],1.0-np.log10(2.0*np.abs(Bz[1:,2]-Bz_exact)/(np.abs(Bz[1:,2])+np.abs(Bz_exact))))
plt.ylabel("Significant Digits of Agreement")
plt.xlabel("Time")
plt.show()

png

Naturally, our simulation is not perfect; no simulation ever will be. However, we can see even as the agreement drops off, it is approaching as asymptote at about 3 SDA, which is quite good for the resolution we chose. If we want, we can take the assessment of our code further with convergence analysis.

Exercise: Convergence testing

Included in the materials for this workshop is the parameter file for a very simple code test using the Alfvén wave. You can change the resolution by modifying the following parameters:

CoordBase::dx
CoordBase::dy
CoordBase::dz

The ideal way to do this is by dividing these numbers by 2 to create a medium-resolution simulation, then dividing by 2 again to create a high-resolution simulation. The output quantity of interest is $B^z$. Run the simulation at each of the three resolutions and plot the difference in $B^z$ between the low and medium resolutions and medium and high resolutions to show that that as we increase the resolution, the simulation results are converging.

(Note: you will need to be careful when subtracting the different results from each other because they each have different numbers of points!)

Key Points

Day 2: General Relativity and GRMHD

Final remarks

Overview

Teaching: min
Exercises: min

Topics

Objectives

Use the break layout for placeholder episodes representing coffee breaks and lunches. These episodes do not have exercises, questions, objectives, or key points in their metadata, but must have a “break” field to show how long the break is (in minutes).

Key Points

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	thal	target
0	63	1	3	145	233	1	0	150	0	2.3	0	1	1
1	37	1	2	130	250	0	1	187	0	3.5	0	2	1
2	41	0	1	130	204	0	0	172	0	1.4	2	2	1
3	56	1	1	120	236	0	1	178	0	0.8	2	2	1
4	57	0	0	120	354	0	1	163	1	0.6	2	2	1
5	57	1	0	140	192	0	1	148	0	0.4	1	1	1
6	56	0	1	140	294	0	0	153	0	1.3	1	2	1
7	44	1	1	120	263	0	1	173	0	0.0	2	3	1
8	52	1	2	172	199	1	1	162	0	0.5	2	3	1
9	57	1	2	150	168	0	1	174	0	1.6	2	2	1

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	ca	thal
293	67	1	2	152	212	0	0	150	0	0.8	1	0	3
294	44	1	0	120	169	0	1	144	1	2.8	0	0	1
295	63	1	0	140	187	0	0	144	1	4.0	2	2	3
296	63	0	0	124	197	0	1	136	1	0.0	1	0	2
297	59	1	0	164	176	1	0	90	0	1.0	1	2	1
298	57	0	0	140	241	0	1	123	1	0.2	1	0	3
299	45	1	3	110	264	0	1	132	0	1.2	1	0	3
300	68	1	0	144	193	1	1	141	0	3.4	1	2	3
301	57	1	0	130	131	0	1	115	1	1.2	1	1	3
302	57	0	1	130	236	0	0	174	0	0.0	1	1	2

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	thal	target
0	63	1	3	145	233	1	0	150	0	2.3	0	1	1
1	37	1	2	130	250	0	1	187	0	3.5	0	2	1
2	41	0	1	130	204	0	0	172	0	1.4	2	2	1
3	56	1	1	120	236	0	1	178	0	0.8	2	2	1
4	57	0	0	120	354	0	1	163	1	0.6	2	2	1

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	thal	target
0	64	1	3	145	233	1	0	150	0	2.3	0	1	1
1	38	1	2	130	250	0	1	187	0	3.5	0	2	1
2	42	0	1	130	204	0	0	172	0	1.4	2	2	1
3	57	1	1	120	236	0	1	178	0	0.8	2	2	1
4	58	0	0	120	354	0	1	163	1	0.6	2	2	1

	41	0	1	130	204	0.2	172	0.3	1.4	2	2.1	1.1
0	56	1	1	120	236	1	178	0	0.8	2	2	1
1	57	0	0	120	354	1	163	1	0.6	2	2	1
2	57	1	0	140	192	1	148	0	0.4	1	1	1
3	56	0	1	140	294	0	153	0	1.3	1	2	1
4	44	1	1	120	263	1	173	0	0.0	2	3	1

	0	1	130	204	0.1	0.2	172	0.3	1.4	2	0.4	2.1	1.1
41
56	1	1	120	236	0	1	178	0	0.8	2	0	2	1
57	0	0	120	354	0	1	163	1	0.6	2	0	2	1
57	1	0	140	192	0	1	148	0	0.4	1	0	1	1
56	0	1	140	294	0	0	153	0	1.3	1	0	2	1
44	1	1	120	263	0	1	173	0	0.0	2	0	3	1

	index	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	thal	target
0	0	63	1	3	145	233	1	0	150	0	2.3	0	1	1
1	1	37	1	2	130	250	0	1	187	0	3.5	0	2	1
2	2	41	0	1	130	204	0	0	172	0	1.4	2	2	1
3	3	56	1	1	120	236	0	1	178	0	0.8	2	2	1
4	4	57	0	0	120	354	0	1	163	1	0.6	2	2	1

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	oldpeak	slope	thal	target
0	63	1	3	145	233	1	0	150	2.3	0	1	1
1	37	1	2	130	250	0	1	187	3.5	0	2	1
2	41	0	1	130	204	0	0	172	1.4	2	2	1

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	ca	thal
300	68	1	0	144	193	1	1	141	0	3.4	1	2	3
301	57	1	0	130	131	0	1	115	1	1.2	1	1	3
302	57	0	1	130	236	0	0	174	0	0.0	1	1	2

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	thal	target
0	63	1	3	145	233	1	0	150	0	2.3	0	1	1
1	37	1	2	130	250	0	1	187	0	3.5	0	2	1
2	41	0	1	130	204	0	0	172	0	1.4	2	2	1
3	56	1	1	120	236	0	1	178	0	0.8	2	2	1
4	57	0	0	120	354	0	1	163	1	0.6	2	2	1
5	57	1	0	140	192	0	1	148	0	0.4	1	1	1
6	56	0	1	140	294	0	0	153	0	1.3	1	2	1
7	44	1	1	120	263	0	1	173	0	0.0	2	3	1
8	52	1	2	172	199	1	1	162	0	0.5	2	3	1
9	57	1	2	150	168	0	1	174	0	1.6	2	2	1

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	ca	thal
293	67	1	2	152	212	0	0	150	0	0.8	1	0	3
294	44	1	0	120	169	0	1	144	1	2.8	0	0	1
295	63	1	0	140	187	0	0	144	1	4.0	2	2	3
296	63	0	0	124	197	0	1	136	1	0.0	1	0	2
297	59	1	0	164	176	1	0	90	0	1.0	1	2	1
298	57	0	0	140	241	0	1	123	1	0.2	1	0	3
299	45	1	3	110	264	0	1	132	0	1.2	1	0	3
300	68	1	0	144	193	1	1	141	0	3.4	1	2	3
301	57	1	0	130	131	0	1	115	1	1.2	1	1	3
302	57	0	1	130	236	0	0	174	0	0.0	1	1	2

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	thal	target
0	63	1	3	145	233	1	0	150	0	2.3	0	1	1
1	37	1	2	130	250	0	1	187	0	3.5	0	2	1
2	41	0	1	130	204	0	0	172	0	1.4	2	2	1
3	56	1	1	120	236	0	1	178	0	0.8	2	2	1
4	57	0	0	120	354	0	1	163	1	0.6	2	2	1

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	thal	target
0	64	1	3	145	233	1	0	150	0	2.3	0	1	1
1	38	1	2	130	250	0	1	187	0	3.5	0	2	1
2	42	0	1	130	204	0	0	172	0	1.4	2	2	1
3	57	1	1	120	236	0	1	178	0	0.8	2	2	1
4	58	0	0	120	354	0	1	163	1	0.6	2	2	1

	41	0	1	130	204	0.2	172	0.3	1.4	2	2.1	1.1
0	56	1	1	120	236	1	178	0	0.8	2	2	1
1	57	0	0	120	354	1	163	1	0.6	2	2	1
2	57	1	0	140	192	1	148	0	0.4	1	1	1
3	56	0	1	140	294	0	153	0	1.3	1	2	1
4	44	1	1	120	263	1	173	0	0.0	2	3	1

	0	1	130	204	0.1	0.2	172	0.3	1.4	2	0.4	2.1	1.1
41
56	1	1	120	236	0	1	178	0	0.8	2	0	2	1
57	0	0	120	354	0	1	163	1	0.6	2	0	2	1
57	1	0	140	192	0	1	148	0	0.4	1	0	1	1
56	0	1	140	294	0	0	153	0	1.3	1	0	2	1
44	1	1	120	263	0	1	173	0	0.0	2	0	3	1

	index	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	thal	target
0	0	63	1	3	145	233	1	0	150	0	2.3	0	1	1
1	1	37	1	2	130	250	0	1	187	0	3.5	0	2	1
2	2	41	0	1	130	204	0	0	172	0	1.4	2	2	1
3	3	56	1	1	120	236	0	1	178	0	0.8	2	2	1
4	4	57	0	0	120	354	0	1	163	1	0.6	2	2	1

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	oldpeak	slope	thal	target
0	63	1	3	145	233	1	0	150	2.3	0	1	1
1	37	1	2	130	250	0	1	187	3.5	0	2	1
2	41	0	1	130	204	0	0	172	1.4	2	2	1

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	ca	thal
300	68	1	0	144	193	1	1	141	0	3.4	1	2	3
301	57	1	0	130	131	0	1	115	1	1.2	1	1	3
302	57	0	1	130	236	0	0	174	0	0.0	1	1	2

Introduction to High-Performance Computing

Introduction to Supercomputing

Overview

High-Performance Computing

Anatomy of an HPC Cluster

What are the specifications of my computer?

KDE Info Center

Linux Mint Cinnamon System Info

Linux Mint Cinnamon System Info

Advantages of using an HPC cluster for research

Compute nodes

Central Processing Units

CPU Brands and Product lines

Cores

Hyperthreading

CPU Frequency

Cache

Learn to read computer specifications

Intel

AMD

Storage

Network

WVU High-Performance Computer Clusters

Thorny Flat

Dolly Sods

Command Line

Secure Connections

Exercise 1

High-Performance Computing and Geopolitics

Key Points

Command Line Interface

Overview

Command Line Interface

The Shell

The prompt

Why use the Command Line Interface?

Flexibility and automation

Starting with the shell

Arguments

The Unix directory file structure (a.k.a. where am I?)

The “root” directory!

Paths

Using paths with commands

Tab completion

Relative paths

Synopsis of Full versus Relative paths

Copying, creating, moving, and removing data

Copying

Creating

Moving

Renaming

Removing

Exiting from the cluster

10 Unix/Linux commands to learn and use

The echo and cat commands

Folder commands

Commands for copy and move

Delete files and Folders

Summary of Basic Commands

Exercise 1

Command not found

Exercise 2

Exercise 3

Exercise 4

Hint

Grabbing files from the internet

Downloading the Drosophila genome

Working with compressed files, using unzip and gunzip

Wildcards, shortcuts, and other time-saving tricks

Wild cards

Shortcuts

Home directory or “~”

Parent directory or “..”

Current directory or “.”

Command History

Cancel a command or task

Summary: Commands, options, and keystrokes covered

Advanced Bash Commands and Utilities

Configuring your shell

.bashrc versus .bash_profile

The `echo` and `cat` commands

`.bashrc` versus `.bash_profile`

Transferring files with `rsync`

Guillermo Avendaño Franco
Aldo Humberto Romero

Old style String Formatting (The `%` operator)

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	thal	target
0	63	1	3	145	233	1	0	150	0	2.3	0	1	1
1	37	1	2	130	250	0	1	187	0	3.5	0	2	1
2	41	0	1	130	204	0	0	172	0	1.4	2	2	1
3	56	1	1	120	236	0	1	178	0	0.8	2	2	1
4	57	0	0	120	354	0	1	163	1	0.6	2	2	1
5	57	1	0	140	192	0	1	148	0	0.4	1	1	1
6	56	0	1	140	294	0	0	153	0	1.3	1	2	1
7	44	1	1	120	263	0	1	173	0	0.0	2	3	1
8	52	1	2	172	199	1	1	162	0	0.5	2	3	1
9	57	1	2	150	168	0	1	174	0	1.6	2	2	1

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	ca	thal
293	67	1	2	152	212	0	0	150	0	0.8	1	0	3
294	44	1	0	120	169	0	1	144	1	2.8	0	0	1
295	63	1	0	140	187	0	0	144	1	4.0	2	2	3
296	63	0	0	124	197	0	1	136	1	0.0	1	0	2
297	59	1	0	164	176	1	0	90	0	1.0	1	2	1
298	57	0	0	140	241	0	1	123	1	0.2	1	0	3
299	45	1	3	110	264	0	1	132	0	1.2	1	0	3
300	68	1	0	144	193	1	1	141	0	3.4	1	2	3
301	57	1	0	130	131	0	1	115	1	1.2	1	1	3
302	57	0	1	130	236	0	0	174	0	0.0	1	1	2

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	thal	target
0	63	1	3	145	233	1	0	150	0	2.3	0	1	1
1	37	1	2	130	250	0	1	187	0	3.5	0	2	1
2	41	0	1	130	204	0	0	172	0	1.4	2	2	1
3	56	1	1	120	236	0	1	178	0	0.8	2	2	1
4	57	0	0	120	354	0	1	163	1	0.6	2	2	1

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	thal	target
0	64	1	3	145	233	1	0	150	0	2.3	0	1	1
1	38	1	2	130	250	0	1	187	0	3.5	0	2	1
2	42	0	1	130	204	0	0	172	0	1.4	2	2	1
3	57	1	1	120	236	0	1	178	0	0.8	2	2	1
4	58	0	0	120	354	0	1	163	1	0.6	2	2	1

	41	0	1	130	204	0.2	172	0.3	1.4	2	2.1	1.1
0	56	1	1	120	236	1	178	0	0.8	2	2	1
1	57	0	0	120	354	1	163	1	0.6	2	2	1
2	57	1	0	140	192	1	148	0	0.4	1	1	1
3	56	0	1	140	294	0	153	0	1.3	1	2	1
4	44	1	1	120	263	1	173	0	0.0	2	3	1

	0	1	130	204	0.1	0.2	172	0.3	1.4	2	0.4	2.1	1.1
41
56	1	1	120	236	0	1	178	0	0.8	2	0	2	1
57	0	0	120	354	0	1	163	1	0.6	2	0	2	1
57	1	0	140	192	0	1	148	0	0.4	1	0	1	1
56	0	1	140	294	0	0	153	0	1.3	1	0	2	1
44	1	1	120	263	0	1	173	0	0.0	2	0	3	1

	index	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	thal	target
0	0	63	1	3	145	233	1	0	150	0	2.3	0	1	1
1	1	37	1	2	130	250	0	1	187	0	3.5	0	2	1
2	2	41	0	1	130	204	0	0	172	0	1.4	2	2	1
3	3	56	1	1	120	236	0	1	178	0	0.8	2	2	1
4	4	57	0	0	120	354	0	1	163	1	0.6	2	2	1

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	oldpeak	slope	thal	target
0	63	1	3	145	233	1	0	150	2.3	0	1	1
1	37	1	2	130	250	0	1	187	3.5	0	2	1
2	41	0	1	130	204	0	0	172	1.4	2	2	1

	age	sex	cp	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	slope	ca	thal
300	68	1	0	144	193	1	1	141	0	3.4	1	2	3
301	57	1	0	130	131	0	1	115	1	1.2	1	1	3
302	57	0	1	130	236	0	0	174	0	0.0	1	1	2