Matlab: Running Matlab scripts on a HPC cluster¶
This simple tutorial explains how to use Matlab without launching the graphical interface and using the submission script.
Executing Matlab scripts¶
Consider this simple script that computes first and second derivatives of a function to find extrema and inflection points of a given function.
You can create a directory for this, for example MATLAB and uncompress there the file derivatives.zip:
unzip derivatives.zip
It will uncompress a file called “derivatives.m”, that is the actual matlab code that we would like to execute on the cluster.
The submission script is very simple, for this example we will use a single core:
#!/bin/sh
#PBS -N MATLAB
#PBS -l nodes=1:ppn=1
#PBS -l walltime=1:00:00
#PBS -m ae
#PBS -q debug
module purge
module load statistics/matlab/2014a
cd $PBS_O_WORKDIR
matlab -nodisplay -r derivatives
Store this lines into a file called runjob.pbs
This submission script is telling the PBS system that we are creating a job called “MATLAB”, that will use one node (nodes=1) and one core per node (ppn=1), during one hour (walltime=1:00:00). I will be notified by email (-m ae) either for the job being aborted or ended. The queue were the job is submitted is called “debug” but you can also choose other queues such as “comm_mmem_week” or “comm_mmem_day”. that will offer extended periods of time.
The lines module purge and module load statistics/matlab/2014a will prepare the environment for executing Matlab on the HPC cluster.
Finally, the script will execute the matlab script “derivatives.m” without opening the graphical user interface (GUI). Notive that you should execute matlab -nodisplay -r derivatives without adding the “.m”. Matlab will always search for a file called “derivatives.m”
You submit the job from the command line executing:
$qsub runjob.pbs
987788.srih0001.hpc.wvu.edu
You should get like above the JobID, an identifier that allow you to keep track of your execution. You can monitor the execution like this: When in queue, ie, waiting for execution:
$ qstat 987788
Job ID Name User Time Use S Queue
------------------------- ---------------- --------------- -------- - ------
987788.srih0001 MATLAB gufranco 0 Q debug
When running:
$ qstat 987788
Job ID Name User Time Use S Queue
------------------------- ---------------- --------------- -------- - ------
987788.srih0001 MATLAB gufranco 0 R debug
When finished:
$ qstat 987788
Job ID Name User Time Use S Queue
------------------------- ---------------- --------------- -------- - -----
987788.srih0001 MATLAB gufranco 00:00:07 C debug
When the job concludes, you will get the files:
derivatives.fig
derivatives.m
derivatives.png
MATLAB.e987788
MATLAB.o987788
runjob.pbs``
The figures where generated and save on the same folder you submit your job. The output of your execution is stored at MATLAB.o987788
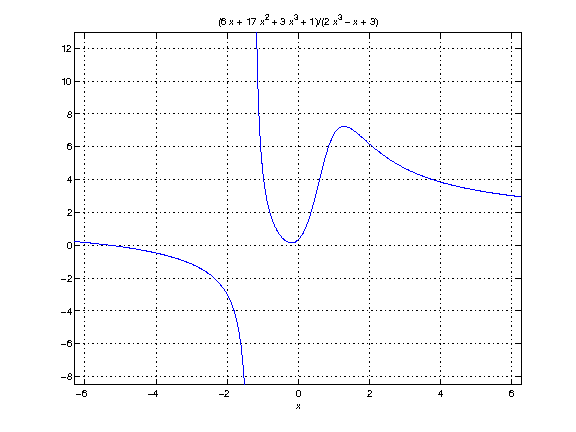
derivatives.png
< M A T L A B (R) >
Copyright 1984-2014 The MathWorks, Inc.
R2014a (8.3.0.532) 64-bit (glnxa64)
February 11, 2014
To get started, type one of these: helpwin, helpdesk, or demo.
For product information, visit www.mathworks.com.
First Derivatives: Finding Local Minima and Maxima
==================================================
f =
(3*x^3 + 17*x^2 + 6*x + 1)/(2*x^3 - x + 3)
ans =
3/2
ans =
3/2
ans =
- 1/(6*(3/4 - (241^(1/2)*432^(1/2))/432)^(1/3)) - (3/4 - (241^(1/2)*432^(1/2))/432)^(1/3)
ans =
-1.2896
First Derivative: Local extremum Points
=======================================
g =
(9*x^2 + 34*x + 6)/(2*x^3 - x + 3) - ((6*x^2 - 1)*(3*x^3 + 17*x^2 + 6*x + 1))/(2*x^3 - x + 3)^2
ans =
((2841*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(1/3))/1156 + 9*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(2/3) + 361/289)^(1/2)/(6*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(1/6)) + ((337491*6^(1/2)*((3*3^(1/2)*178939632355^(1/2))/9826 + 2198209/9826)^(1/2))/39304 + (2841*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(1/3)*((2841*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(1/3))/1156 + 9*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(2/3) + 361/289)^(1/2))/578 - 9*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(2/3)*((2841*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(1/3))/1156 + 9*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(2/3) + 361/289)^(1/2) - (361*((2841*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(1/3))/1156 + 9*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(2/3) + 361/289)^(1/2))/289)^(1/2)/(6*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(1/6)*((2841*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(1/3))/1156 + 9*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(2/3) + 361/289)^(1/4)) - 15/68
((2841*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(1/3))/1156 + 9*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(2/3) + 361/289)^(1/2)/(6*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(1/6)) - ((337491*6^(1/2)*((3*3^(1/2)*178939632355^(1/2))/9826 + 2198209/9826)^(1/2))/39304 + (2841*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(1/3)*((2841*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(1/3))/1156 + 9*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(2/3) + 361/289)^(1/2))/578 - 9*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(2/3)*((2841*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(1/3))/1156 + 9*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(2/3) + 361/289)^(1/2) - (361*((2841*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(1/3))/1156 + 9*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(2/3) + 361/289)^(1/2))/289)^(1/2)/(6*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(1/6)*((2841*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(1/3))/1156 + 9*((3^(1/2)*178939632355^(1/2))/176868 + 2198209/530604)^(2/3) + 361/289)^(1/4)) - 15/68
ans =
1.2860
-0.1892
Second Derivatives: Finding Inflection Points
=============================================
h =
(18*x + 34)/(2*x^3 - x + 3) - (2*(6*x^2 - 1)*(9*x^2 + 34*x + 6))/(2*x^3 - x + 3)^2 - (12*x*(3*x^3 + 17*x^2 + 6*x + 1))/(2*x^3 - x + 3)^2 + (2*(6*x^2 - 1)^2*(3*x^3 + 17*x^2 + 6*x + 1))/(2*x^3 - x + 3)^3
ans =
1.8651543689917122385037075917613
0.57871842655441748319601085860196
Using the Matlab Compiler¶
The first step is to load matlab to get access to its executables:
module load statistics/matlab/2014a
Prepare the compilation environment with:
$ mbuild -setup``
MBUILD configured to use 'gcc' for C language compilation.``
To choose a different language, execute one from the following:``
mex -setup C++ -client MBUILD ``
mex -setup FORTRAN -client MBUILD``
You cannot compile matlab scripts that uses the symbolic toolbox
https://www.mathworks.com/products/ineligible_programs.html
So we will use another script for this tutorial.
After uncompress the file “mandelbrot.m”:
mcc -m mandelbrot.m
It takes a while, when finished you will get some extra files:
mandelbrot
run_mandelbrot.sh
The submission script changes to:
#!/bin/sh
#PBS -N MATLAB
#PBS -l nodes=1:ppn=1
#PBS -l walltime=1:00:00
#PBS -m ae
#PBS -q debug
module purge
module load statistics/matlab/2014a
cd $PBS_O_WORKDIR
./run_mandelbrot.sh /shared/software/MATLAB/R2014a
After submit the job with:
qsub runjob.pbs
You get the results on “MATLAB.o#######” with the corresponding JobID
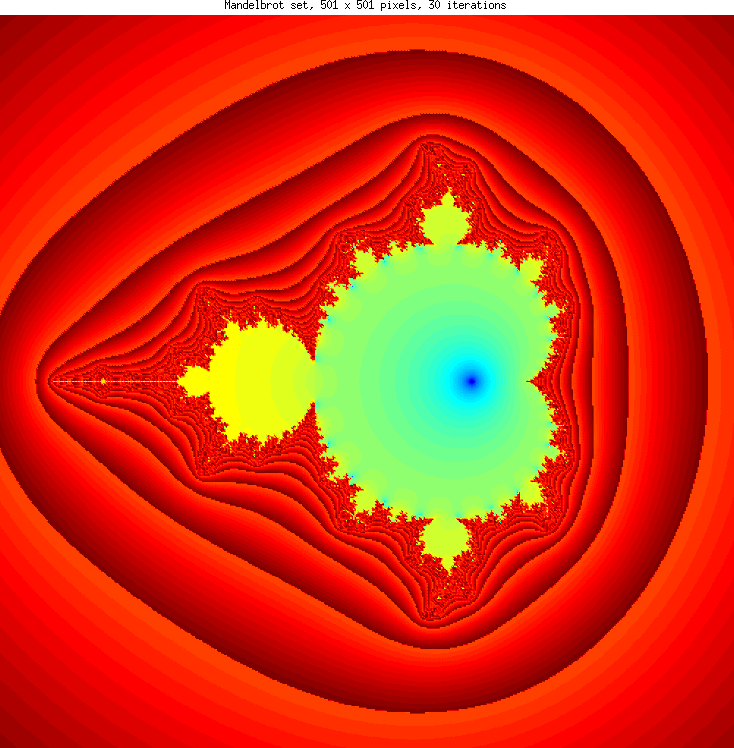
Mandelbrot fractal generated from Matlab