This lesson is being piloted (Beta version)

Interactive Applications in Python

Shiny for Python

Overview

Teaching: 60 min
Exercises: 0 min
Questions

  • Create highly interactive visualizations, realtime dashboards, data explorers, model demos, all in pure Python

Objectives

  • First learning objective. (FIXME)

Introduction

Shiny is a software package for building interactive web applications. Originally created for the R language, it has been now expanded to support Python Language. We will focus here on Shiny for Python. Most of the internals of Shiny are shared between the two implementations.

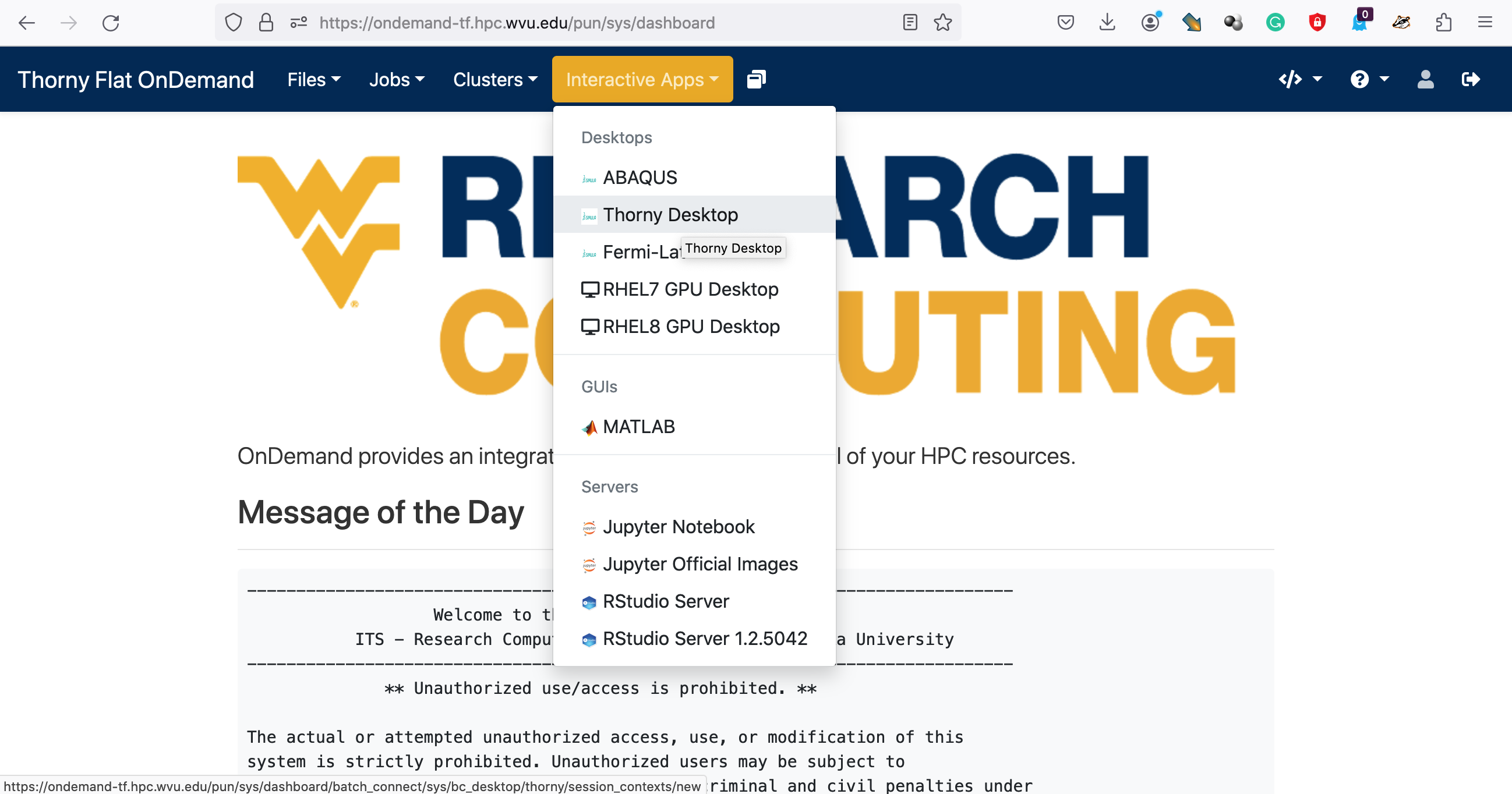
We start our exploration of shiny creating a virtual desktop on Thorny Flat using Open On-demand. Goto to Open On-Demand portal for Thorny Flat. Enter your credentials. From the dashboard select “Interactive Apps” and “Thorny Desktop”

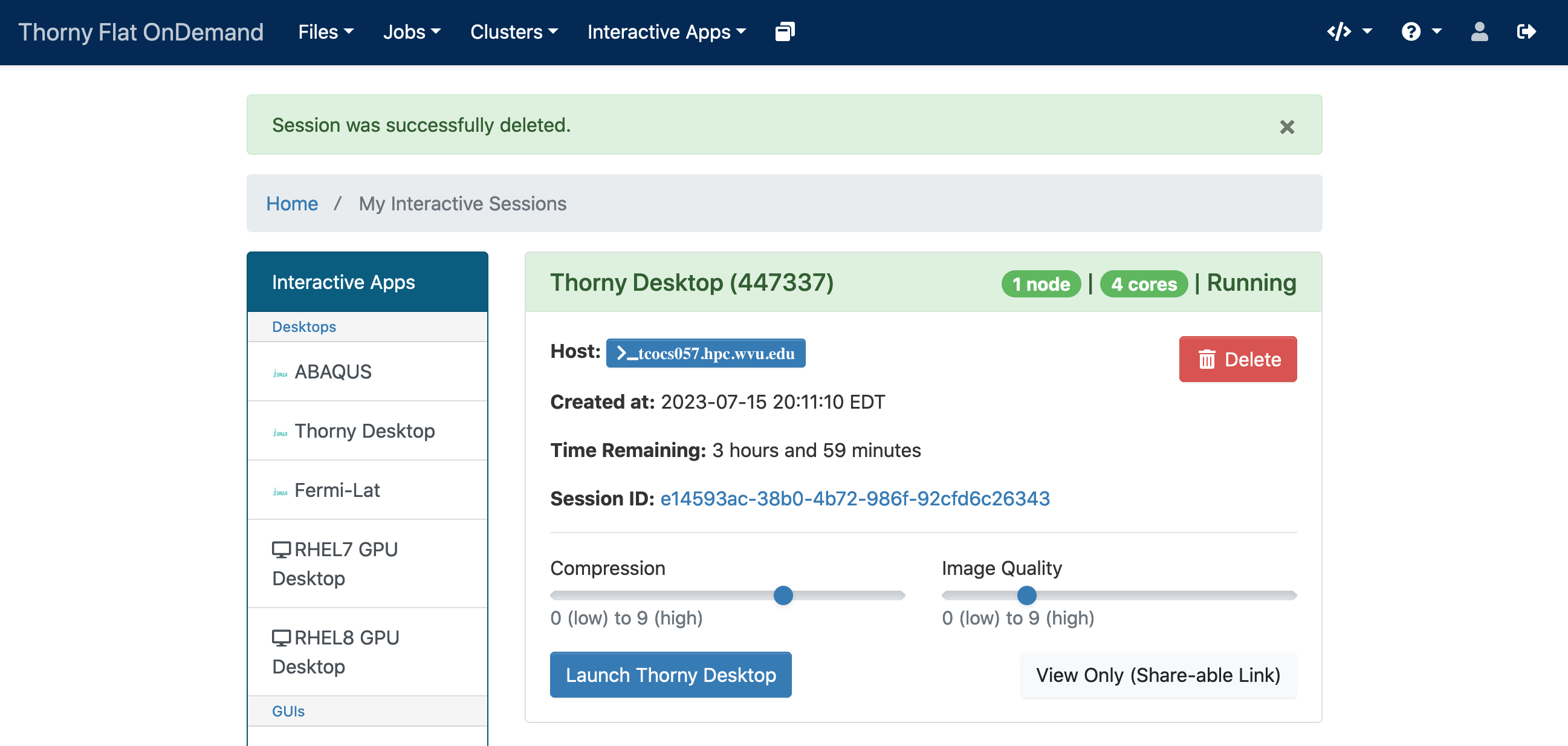
Open On-Demand

Select minimal requests such as “standby” for partition, 4 hours walltime, 4 CPU cores. A new job will be created

Open On-Demand

Click on “Launch Thorny Desktop” and open 2 windows, a terminal, and a web browser.

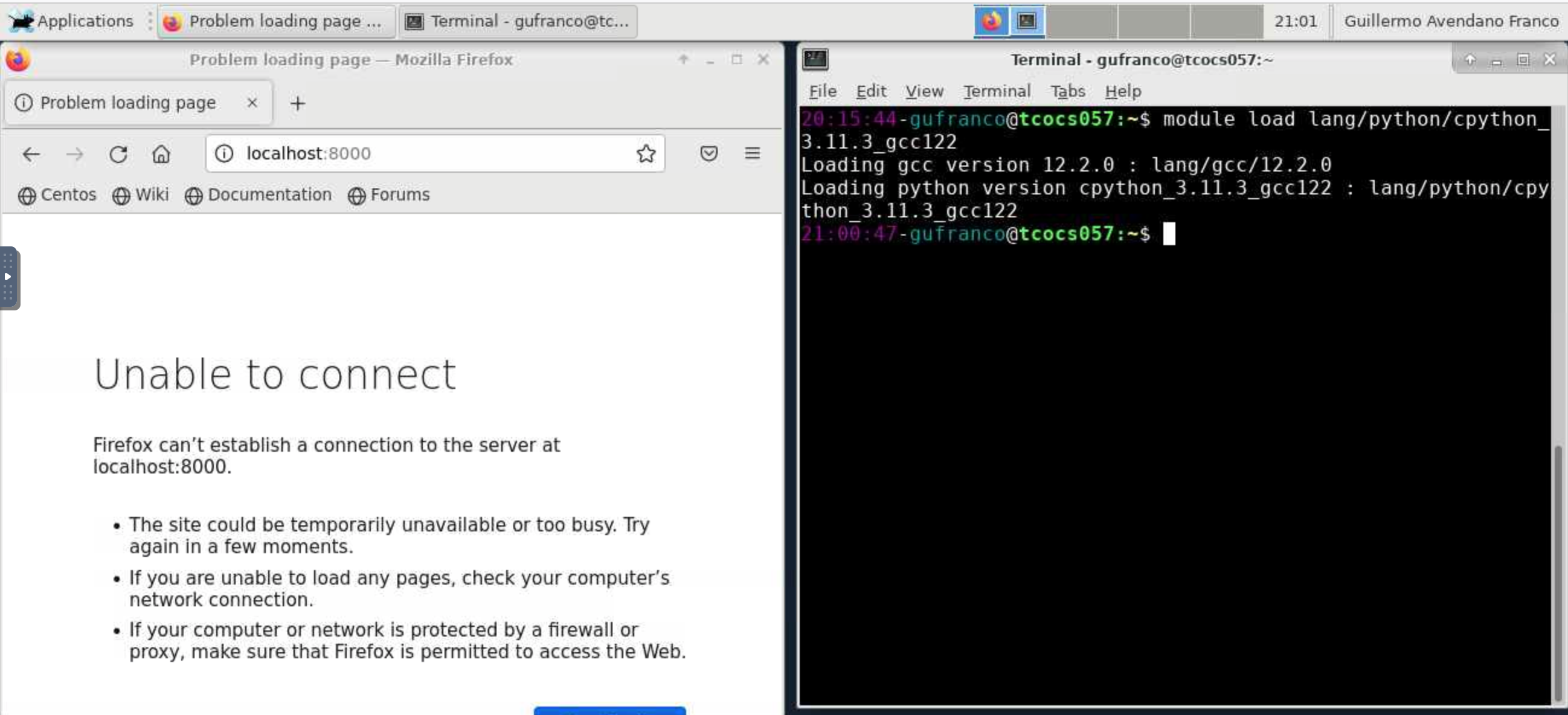
Open On-Demand

Load the module for Python on the terminal

$> module load lang/python/cpython_3.11.3_gcc122

Now we are ready to create our first shiny app.

Create a folder for our shiny apps. Lets call it SHINY and inside create a folder app1

$> mkdir -p SHINY/app1
$> cd SHINY/app1

Now we can create a simple example app with the command::

$> shiny create .

Run the first app with:

$> shiny run --reload

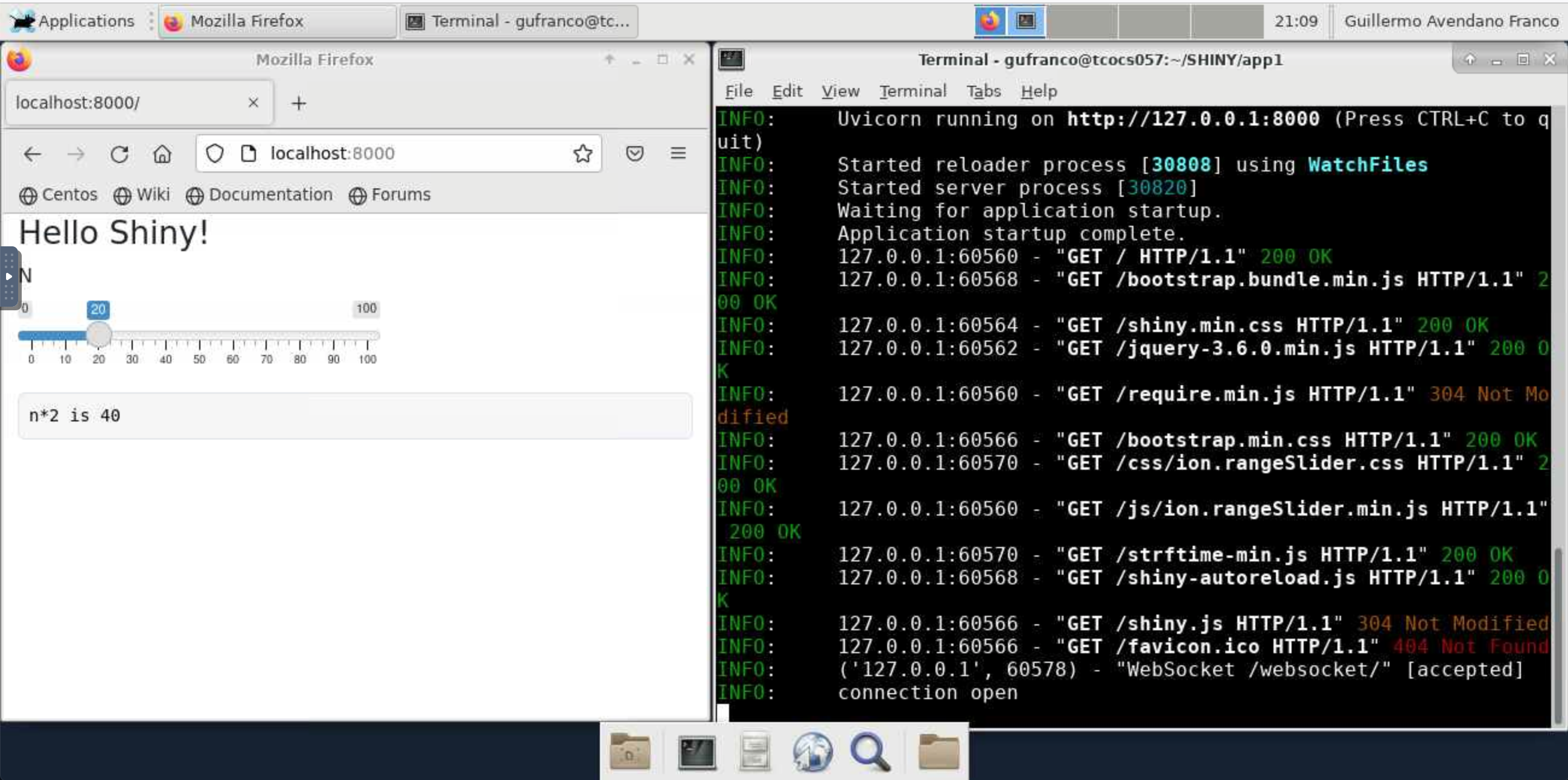
On the web browser go to https://localhost:8000 to visualize the app

Open On-Demand

When we execute shiny create . a python file called app.py is created. This file is as follows:

from shiny import App, render, ui

app_ui = ui.page_fluid(
  ui.h2("Hello Shiny!"),
  ui.input_slider("n", "N", 0, 100, 20),
  ui.output_text_verbatim("txt"),
)

def server(input, output, session):
  @output
  @render.text
  def txt():
      return f"n*2 is {input.n() * 2}"

app = App(app_ui, server)

This file contains the main ingredients of a shiny app. Shiny applications consist of two parts: the user interface (or UI), and the server function. These are combined using a shiny.App object.

Adding UI inputs and outputs

Note the two UI pieces added:

These elements have been added to the app_ui()

We can now copy this app and start adding modifications to it to construct our second app. Cancel the execution of the first app executing ^C, move one folder up, and copy the folder under a new name.

$> cd ..
$> cp -r app1 app2
$> cd app2

Change the file app.py inside app2 as follows:

from shiny import App, render, ui

app_ui = ui.page_fluid(
    ui.h2("Sum Shiny!"),
    ui.input_slider("a", "A", 0, 100, 20),
    ui.input_slider("b", "B", 0, 100, 20),
    ui.output_text_verbatim("txt"),
)

def server(input, output, session):
    @output
    @render.text
    def txt():
        return f"a+b is {input.a() + input.b()}"

app = App(app_ui, server)

Now we have two sliders and one verbatim text. These elements are created as part of the app_ui() function.

The UI part defines what visitors will see on their web page. The dynamic parts of our app happen inside the server function.

Inside the server function, we define an output function named txt. This output function provides the content for the output_text_verbatim(“txt”) in the UI.

Note that inside the server function, we do the following:

Finally, notice our txt() function takes the value of our sliders a and b, and returns its sum computed inside the txt function. To access the value of the sliders, we use input.a() and input.b(). Notice that these are callable objects (like a function) that must be invoked to get the value.

Reactivity

This reactive flow of data from UI inputs to server code, and back out to UI outputs is central to how Shiny works.

When you moved the sliders in the app, a series of actions were kicked off, resulting in the output on the screen changes. This is called reactivity.

Inputs, like our sliders a and b, are reactive values: when they change, they automatically cause any of the reactive functions that use them (like txt()) to recalculate.

Layouts

So far, our UI has consisted of two inputs and one output. Shiny also has layout components that can contain other components and visually arrange them. Examples of these are sidebar layouts, tab navigation, and cards.

For our next example, we’ll use a common layout strategy for simple Shiny apps. We will have input controls in a narrow sidebar on the left and a plot on the right.

In the following code, we use the function ui.layout_sidebar() to separate the page into two panels. This function takes two arguments: a ui.panel_sidebar and a ui.panel_main, which each can contain whatever components you want to display on the left and right, respectively.

import matplotlib.pyplot as plt
import numpy as np
from shiny import ui, render, App

# Create some random data
t = np.linspace(0, 2 * np.pi, 1024)
data2d = np.sin(t)[:, np.newaxis] * np.cos(t)[np.newaxis, :]

app_ui = ui.page_fixed(
    ui.h2("Playing with colormaps"),
    ui.markdown("""
	This app is based on a [Matplotlib example][0] that displays 2D data
	with a user-adjustable colormap. We use a range slider to set the data
	range that is covered by the colormap.

	[0]: https://matplotlib.org/3.5.3/gallery/userdemo/colormap_interactive_adjustment.html
    """),
    ui.layout_sidebar(
	ui.panel_sidebar(
	    ui.input_radio_buttons("cmap", "Colormap type",
		dict(viridis="Perceptual", gist_heat="Sequential", RdYlBu="Diverging")
	    ),
	    ui.input_slider("range", "Color range", -1, 1, value=(-1, 1), step=0.05),
	),
	ui.panel_main(
	    ui.output_plot("plot")
	)
    )
)

def server(input, output, session):
    @output
    @render.plot
    def plot():
	fig, ax = plt.subplots()
	im = ax.imshow(data2d, cmap=input.cmap(), vmin=input.range()[0], vmax=input.range()[1])
	fig.colorbar(im, ax=ax)
	return fig


app = App(app_ui, server)

Notice how Shiny uses nested function calls to indicate parent/child relationships. In this example, ui.input_radio_buttons() is inside of ui.panel_sidebar(), and ui.panel_sidebar() is in ui.layout_sidebar(), and so on.

app_ui = ui.page_fixed(
  ui.h2(...),
  ui.markdown(...),
  ui.layout_sidebar(
    ui.panel_sidebar(
      ui.input_radio_buttons(...),
      ui.input_slider(...),
      ),
    ui.panel_main(
      ui.output_plot(...)
    )
  )
)

This example also includes a title and some explanatory text written in a Markdown string literal, and uses the ui.markdown() function to render it to HTML.

UI elements for inputs

Now we will explore in more detail the creation of UI elements separated from the server logic.

Each input control on a page is created by calling a Python function. All such functions take the same first two string arguments:

Note that many inputs take additional arguments. Lets see some of the UI elements from our previous apps:

  ui.input_slider("a", "A", 0, 100, 20),
  
  ui.input_slider("b", "B", 0, 100, 20),

  ui.input_radio_buttons("cmap", "Colormap type",
		  dict(viridis="Perceptual", gist_heat="Sequential", RdYlBu="Diverging"))

  ui.input_slider("range", "Color range", 
    -1, 1, value=(-1, 1), step=0.05),

So far we have only use input_slider and , input_radio_buttons, but there are many other UI elements. We’ll show some common input objects.

Number inputs

ui.input_numeric creates a text box where a number (integer or real) can be entered, plus up/down buttons. This is most useful when you want the user to be able to enter an exact value.

ui.input_slider creates a slider. Compared to a numeric input, a slider makes it easier to scrub back and forth between values, so it may be more appropriate when the user does not have an exact value in mind to start with. You can also provide more restrictions on the possible values, as the min, max, and step size are all strictly enforced.

ui.input_slider can also be used to select a range of values. To do so, pass a tuple of two numbers as the value argument instead of a single number.

Example (4.Number_Inputs/app.py):

from shiny import ui, App

app_ui = ui.page_fluid(
    ui.input_numeric("x1", "Number", value=10),
    ui.input_slider("x2", "Slider", value=10, min=0, max=20),
    ui.input_slider("x3", "Range slider", value=(6, 14), min=0, max=20)
)

app = App(app_ui, None)

Text inputs

Shiny includes three inputs for inputting string values.

ui.input_text This is a simple textfield. Use it for shorter, single-line values.

ui.input_text_area displays multiple lines, soft-wraps the text, and lets the user include line breaks, so is more appropriate for longer runs of text or multiple paragraphs.

ui.input_password is for passwords and other values that should not be displayed in the clear. (Note that Shiny does not apply any encryption to the password, so if your app involves passing sensitive information, make sure your deployed app uses https, not http, connections.)

Example (5.Text_Inputs/app.py):

from shiny import ui, App

app_ui = ui.page_fluid(
    ui.input_text("x1", "Text", placeholder="Enter text"),
    ui.input_text_area("x2", "Text area", placeholder="Enter text"),
    ui.input_password ("x3", "Password", placeholder="Enter password"),
)

app = App(app_ui, None)

Selection inputs

There are two options for single and multiple selection from a list of values ui.input_selectize and ui.input_select

You can choose whether the user can select multiple values or not, using the multiple argument. ui.input_selectize uses the Selectize JavaScript library. ui.input_select inserts a standard HTML <select> tag.

ui.input_radio_buttons and ui.input_checkbox_group are useful for cases where you want the choices to always be displayed. Radio buttons force the user to choose one and only one option, while checkbox groups allow zero, one, or multiple choices to be selected.

Example (6.Selection_inputs/app.py):

from shiny import ui, App

choices = ["Tetrahedron", "Cube", "Octahedron", "Dodecahedron", "Icosahedron"]

app_ui = ui.page_fluid(
    ui.h2("Platonic Solids"),
    ui.input_selectize("x1", "Selectize (single)", choices),
    ui.input_selectize("x2", "Selectize (multiple)", choices, multiple = True),
    ui.input_select("x3", "Select (single)", choices),
    ui.input_select("x4", "Select (multiple)", choices, multiple = True),
    ui.input_radio_buttons("x5", "Radio buttons", choices),
    ui.input_checkbox_group("x6", "Checkbox group", choices),
)

app = App(app_ui, None)

Toggle inputs

Toggles allow the user to specify whether something is true/false (or on/off, enabled/disabled, included/excluded, etc.).

ui.input_checkbox shows a simple checkbox, while ui.input_switch shows a toggle switch. These are functionally identical, but by convention, checkboxes should be used when part of a form that has a Submit or Continue button, while toggle switches should be used when they take immediate effect.

Example (7.Toggle_inputs/app.py)

from shiny import ui, App

app_ui = ui.page_fluid(
    ui.input_checkbox("x1", "Checkbox"),
    ui.input_switch("x2", "Switch")
)

app = App(app_ui, None)

Date inputs

There are two inputs for dates:

Example (8.Date_inputs/app.py):

from shiny import ui, App

app_ui = ui.page_fluid(
    ui.input_date("x1", "Date input"),
    ui.input_date_range("x2", "Date range input"),
)

app = App(app_ui, None)

Action inputs

ui.input_action_button and ui.input_action_link let the user invoke specific actions on the server side.

Use ui.input_action_button for actions that feels effectual: recalculating, fetching new data, applying settings, etc. Add class_=”btn-primary” to highlight important actions (like Submit or Continue), and class_=”btn-danger” to highlight dangerous actions (like Delete).

Use ui.input_action_link for actions that feel more like navigation, like exposing a new UI panel, navigating through paginated results, or bringing up a modal dialog.

Example (9.Action_inputs/app.py):

from shiny import ui, App

app_ui = ui.page_fluid(
    ui.p(ui.input_action_button("x1", "Action button")),
    ui.p(ui.input_action_button("x2", "Action button (Primary)", class_="btn-primary")),
    ui.p(ui.input_action_button("x3", "Action button (Danger)", class_="btn-danger")),
    ui.p(ui.input_action_link("x4", "Action link")),
)

app = App(app_ui, None)

UI elements for outputs

Outputs create a spot on the webpage to put results from the server.

At a minimum, all UI outputs require an id argument, which corresponds to the server’s output ID.

For example if you create this UI output:

ui.output_text("my_func")

You need a decorated function my_func on the server side. Something like:

def server(input, output, session):
    @output
    @render.text
    def my_func():
        return "The result of simulation is ..."

Notice that the name of the function my_func() matches the output ID; this is how Shiny knows how to connect each of the UI’s outputs with its corresponding logic in the server.

Notice also the relationship between the names ui.output_text() and the decorator @render.text. Shiny outputs generally follow this pattern of ui.output_XXX() for the UI and @render.XXX to decorate the output logic.

There are two kinds of renderings. Static and Interactive. With Static outputs you will not react to user interaction while for interactive outputs, the user can trigger reactions on the element.

Static plot output

Render static plots based on Matplotlib with ui.output_plot() and @render.plot. Plotting libraries built on Matplotlib, like seaborn and plotnine are also supported.

The function that @render.plot decorates typically returns a Matplotlib Figure or plotnine ggplot object, but @render.plot does support other less common return types, and also supports plots generated through side-effects.

Example (10.Static_plot/app.py):

import numpy as np
from shiny import ui, render, App
from matplotlib import pyplot as plt

app_ui = ui.page_fluid(
        ui.h2("Random points on scatter plot"),
        ui.input_slider("n", "Number of Points", value=50, min=10, max=100, step=10),
        ui.output_plot("a_scatter_plot"),
)

def server(input, output, session):
        @output
        @render.plot
        def a_scatter_plot():
                x = np.random.rand(input.n())
                y = np.random.rand(input.n())
                return plt.scatter(x,y)

app = App(app_ui, server)

Simple table output

Render various kinds of data frames into an HTML table with ui.output_table() and @render.table.

The function that @render.table decorates typically returns a pandas.DataFrame, but object(s) that can be coerced to a pandas.DataFrame via an obj.to_pandas() method are also supported (this includes Polars data frames and Arrow tables).

Example (11.Table_outpu/app.py):

from pathlib import Path
import pandas as pd
from shiny import ui, render, App

df = pd.read_csv(Path(__file__).parent / "iris.csv")

app_ui = ui.page_fluid(
    ui.h2("Iris Dataset"),
    ui.output_table("iris_dataset"),
)

def server(input, output, session):
    @output
    @render.table
    def iris_dataset():
        return df

app = App(app_ui, server)

This example requires the packages pandas for converting the CSV file into a pandas dataframe and jinja2 displaying the table.

Interactive plots

Shiny supports interactive plotting libraries such as plotly. Here’s a basic example using plotly:

from shiny import ui, App
from shinywidgets import output_widget, render_widget
import plotly.express as px
import plotly.graph_objs as go

df = px.data.iris()

app_ui = ui.page_fluid(
    ui.h2("Iris Dataset"),
    ui.div(
        ui.input_select(
            "x", label="Variable",
            choices=['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
        ),
        ui.input_select(
            "color", label="Color",
            choices=["species"]
        ),
        class_="d-flex gap-3"
    ),
    output_widget("my_widget")
)

def server(input, output, session):
    @output
    @render_widget
    def my_widget():
        fig = px.histogram(
            df, x=input.x(), color=input.color(),
            marginal="rug"
        )
        fig.layout.height = 275
        return fig

app = App(app_ui, server)

For running this example we need the packages plotly and shinywidgets.

Interactive maps

Shiny supports interactive mapping libraries such as ipyleaflet, pydeck, and more. Here’s a basic example using ipyleaflet with a few basemaps:

Example (13.Interactive_maps/app.py):

from shiny import *
from shinywidgets import output_widget, render_widget
import ipyleaflet as L

basemaps = {
  "OpenStreetMap": L.basemaps.OpenStreetMap.Mapnik,
  "Stamen.Toner": L.basemaps.Stamen.Toner,
  "Stamen.Terrain": L.basemaps.Stamen.Terrain,
  "Stamen.Watercolor": L.basemaps.Stamen.Watercolor,
  "Esri.WorldImagery": L.basemaps.Esri.WorldImagery,
  "Esri.NatGeoWorldMap": L.basemaps.Esri.NatGeoWorldMap,
}

app_ui = ui.page_fluid(
    ui.h2("West Virginia - Mountaineer Country"),
    ui.input_select(
        "basemap", "Choose a basemap",
        choices=list(basemaps.keys())
    ),
    output_widget("map")
)

def server(input, output, session):
    @output
    @render_widget
    def map():
        basemap = basemaps[input.basemap()]
        return L.Map(basemap=basemap, center=[39.6, -79.9], zoom=10)

app = App(app_ui, server)

Text output

Use ui.output_text() and the correspoding decorators @render.text to render a block of text. Your server logic should return a Python string. No HTML markup or Markdown can be used, the text will be displayed without processing.

Example (14.Text_output/app.py`):

from shiny import ui, render, App

app_ui = ui.page_fluid(
    ui.output_text("my_cool_text")
)

def server(input, output, session):
    @output
    @render.text
    def my_cool_text():
        return "hello, world!"

app = App(app_ui, server)

There is also the variant ui.output_text_verbatim with the same decorator @render.text. This is similar to text output, but renders text in a monospace font, and respects newlines and multiple spaces (unlike ui.output_text(), which collapses all whitespace into a single space, in accordance with HTML’s normal whitespace rule).

Example (15.Text_verbatim_output/app.py):

from shiny import ui, render, App
import scipy.special

app_ui = ui.page_fluid(
    ui.output_text_verbatim("a_code_block"),
    # The p-3 CSS class is used to add padding on all sides of the page
    class_="p-3"
)

def server(input, output, session):
    @output
    @render.text
    def a_code_block():
        # This function should return a string
        return scipy.special.__doc__

app = App(app_ui, server)

HTML and UI output

ui.output_ui() and decorator @render.ui are used to render HTML and UI from the server.

You’ll need to use output_ui if you want to render HTML/UI dynamically–that is, if you want the HTML to change as inputs and other reactives change.

Example (16.HTML_UI_output/app.py):

from shiny import ui, render, App

app_ui = ui.page_fluid(
    ui.input_text("message", "Message", value="Hello, world!"),
    ui.input_checkbox_group("styles", "Styles", choices=["Bold", "Italic"]),
    ui.input_selectize("size", "HTML font size", choices=["H1", "H2", "H3", "H4"]),
    # The class_ argument is used to enlarge and center the text
    ui.output_ui("some_html", class_="display-3 text-center")
)

def server(input, output, session):
    @output
    @render.ui
    def some_html():
        x = input.message()
        if "Bold" in input.styles():
            x = ui.strong(x)
        if "Italic" in input.styles():
            x = ui.em(x)
        if "H1" in input.size():
            x = ui.h1(x)
        if "H2" in input.size():
            x = ui.h2(x)
        if "H3" in input.size():
            x = ui.h3(x)
        if "H4" in input.size():
            x = ui.h4(x)
        return x

app = App(app_ui, server)

The function under the decorator @render.ui can return any of the following:

Server logic

In Shiny, the server logic is defined within a function which takes three arguments: input, output, and session. It looks something like this:

def server(input, output, session):
    # Server code goes here
    ...

All of the server logic we’ll discuss, such as using inputs and define outputs, happens within the server function.

Each time a user connects to the app, the server function executes once — it does not re-execute each time someone moves a slider or clicks on a checkbox. So how do updates happen? When the server function executes, it creates a number of reactive objects that persist as long as the user stays connected — in other words, as long is their session is active. These reactive objects are containers for functions that automatically re-execute in response to changes in inputs.

Defining outputs

To define the logic for an output, create a function with no parameters whose name matches a corresponding output ID in the UI. Then apply a render decorator and the @output decorator.

As the function is inside the server and the server has input and output objects, these objects are visible inside the server. However, input values can not be read at the top level of the server function. If you try to do that, you’ll get an error that says RuntimeError: No current reactive context. The input values are reactive and, as the error suggests, are only accessible within reactive code.

Consider this example (``17.server_logic/app.py`):

from shiny import App, render, ui

app_ui = ui.page_fluid(
    ui.input_checkbox("enable", "Enable?"),
    ui.h3("Is it enabled?"),
    ui.output_text_verbatim("txt"),
)

def server(input, output, session):
    @output
    @render.text
    def txt():
        if input.enable():
            return "Yes!"
        else:
            return "No!"

app = App(app_ui, server)

When you define an output function, Shiny makes it reactive, and so it can be used to access input values.

Key Points

  • First key point. Brief Answer to questions. (FIXME)

PyVista

Overview

Teaching: 60 min
Exercises: 0 min
Questions

  • 3D plotting and mesh analysis with Python

Objectives

  • First learning objective. (FIXME)

FIXME

Key Points

  • First key point. Brief Answer to questions. (FIXME)

PyMunk

Overview

Teaching: 60 min
Exercises: 0 min
Questions

  • Pythonic 2d physics library for physics demos

Objectives

  • Learn the foundations of pymunk for creating 2D physical simulations of interacting bodies

Introduction to Pymunk

This lesson is intended to provide educators an introduction to Pymunk, a Python package that can create interactive kinematics simulations in two dimensions. Using this package, an educator can create simulations that demonstrate basics physics concepts like energy and momentum; these simulations can be modified by students in order to gain a deeper understanding of the underlying concepts. By using computer simulations, it is possible to let students explore more intricate systems than they might otherwise due to factors such as a limited number of physical setups. It can be especially helpful simulating systems that tend to produce incredibly noisy data when done with physical equipment.

Pymunk

Pymunk is a software package that provides accessible tools to perform simulations of classical physical systems in two dimension. It is object-oriented; that is, it has classes like Space, Body, Shape, and Constraint. We will be thus be constructing objects that belong to these classes. These objects then have properties (e.g. Body has properties like mass and moment of intertia) as well as methods that will allow us to access and change those properties.

A note on units

The units in Pymunk do not represent anything physical but are merely arbitrary units. As such, it is not critical to use familiar values from real-world physics. It is often much more useful to use arbitrary values, adjusting them as we test our code to ensure that a viewer can readily understand the visualized output of the simulation.

The basics

Space

One of the most important concepts in Pymunk is the Space object. This is the two-dimensional region in which our simulation will take place, and almost every simulation will start by constructing this object:

space = pymunk.Space() # This does not usually take in arguments

Next it is important to set the gravity in the space:

space.gravity = (x,y)

Note that this function takes in two arguments, representing the strength of a uniform gravitational field in the $x$ and $y$ directions, respectively. Typically, if we are representing a top-down view of a system, both of these values will be zero; if we are representing a side-on view of a system, $x$ will be 0 and $y$ will be negative, representing a downward pull.

Bodies

Once we have a Space, we will populate it with bodies. When we construct these, we can provide their mass, moment of inertia. By default, these bodies are DYNAMIC, moving around and reacting to forces. However, we can also make STATIC bodies that cannot move.

Shapes

Unless a body is a point mass, we must construct a shape associated with it. This shape defines the physical extent of the body, which is important for collisions. This object also has the friction property, allowing control over the coefficient of kinetic friction. Pymunk uses the Coulomb friction model that is commonly taught in introductory physics courses, where the force due to friction is $F_f = \mu_k F_N$, where $\mu_k$ is the coefficient of kinetic friction and $F_N$ is the normal force.

Installing Pymunk

This notebook assumes that the user has already installed Python as well as Pymunk and its requirements. If this is being used on WVU’s Thorny Flat cluster using OnDemand with the most recent version of Python, this will already be the case. Otherwise, you must install it yourself.

Once python is installed, Pymunk can be installed with pip install pymunk

If you want to use Pymunk with Conda, use the command conda install -c conda-forge pymunk

Getting Started

We will start with a basic simulation of two balls colliding to introduce the essential functions in Pymunk. By doing this experiment computationally, we are able to eliminate several common sources of error that we would encounter in the real world, such as friction or performing the experiment on an uneven surface.

Here, we will establish the basic approach that we will follow throughout the other examples.

  1. Establish the space
  2. Define bodies, give them shapes, and then add them to the space
  3. Step the simulation forward in time, animating it
%reset -f
%matplotlib notebook
import pymunk as pm
from pymunk.vec2d import Vec2d
import matplotlib.pyplot as plt
import pymunk.matplotlib_util as pmplt
from matplotlib import animation as anm

space = pm.Space()
# space.gravity = (-500,0)
collision_elasticity = 1.0 # ranges from 0 (perfectly inelastic) to 1 (perfectly elastic)

mass1 = 10
radius1 = 10
ball1_body = pm.Body(mass=mass1,moment=pm.moment_for_circle(mass1, 0, radius1, (0,0)))
ball1_body.position = (100,100)
ball1_body.start_position = Vec2d(*ball1_body.position)
# ball1_body.apply_impulse_at_local_point(Vec2d(+12000, 0))
ball1_shape = pm.Circle(ball1_body,radius1)
ball1_shape.elasticity = collision_elasticity
space.add(ball1_body,ball1_shape)

mass2 = 10
radius2 = 10
ball2_body = pm.Body(mass=mass2,moment=pm.moment_for_circle(mass2, 0, radius2, (0,0)))
ball2_body.position = (250,100)
ball2_body.start_position = Vec2d(*ball2_body.position)
ball2_shape = pm.Circle(ball2_body,radius2)
ball2_shape.elasticity = collision_elasticity
space.add(ball2_body,ball2_shape)

fig = plt.figure()
ax = plt.axes(xlim=(0, 500), ylim=(0, 200))
ax.set_aspect("equal")
o = pmplt.DrawOptions(ax)
# space.debug_draw(o)
space.shapes[0].body.apply_impulse_at_local_point((5000,0))


def init():
    space.debug_draw(o)
    return []

steps_per_second = 200
substeps = 10
def animate(dt):
    for x in range(substeps):
        space.step(1/steps_per_second/substeps)
    ax.clear()
    ax.set_xlim(0,500)
    ax.set_ylim(0,200)
    space.debug_draw(o)
    return []

frames = 150
anim = anm.FuncAnimation(fig, animate, init_func=init,
                               frames=frames, interval=20, blit=False, repeat=False)

<IPython.core.display.Javascript object>

While we can ignore factors like friction and sloped surfaces if we want, we also have the power the change the simulation an environment to mimic these if we so choose.

For example, suppose we wanted to examine how the collision changes if our “table” were sloped to the left. We can simulate this by applying gravity in the $-x$ direction.

We can also use the elasticity parameter of the bodies to explore inelastic, perfectly elastic, and super elastic collisions.

Simple pendulum

Next, we’ll introduce the idea of connecting objects together by making a simple pendulum. We accomplish this using a constraint object, specifically the PinJoint. This allows us to connect two bodies together with a perfectly rigid, massless rod. For this example, we will connect our circle to a static point in space. It is important to note that we must supply coordinates for where on each body we attach the PinJoint; these coordinates are in each bodies own coordinate system. That is, the coordinates for the the connection to space.static_body are the same as for the space as a whole, but the coordinates for the connection to the circle are measured from the center of that circle.

We can also easily explore the damped oscillator by applying damping to the whole space. When we change the damping property of Space, we are periodically reducing the velocity of every body in the space.

%reset -f
%matplotlib notebook
import matplotlib.pyplot as plt
from matplotlib import animation as anm
import pymunk as pm
from pymunk.vec2d import Vec2d
import pymunk.matplotlib_util as pmplt

space = pm.Space()
space.gravity = 0,-9820
# space.damping = 0.2

mass = 10
radius = 25
body = pm.Body(mass,pm.moment_for_circle(mass, 0, radius, (0,0)))
body.position = (300, 175)
body.start_position = Vec2d(*body.position)
shape = pm.Circle(body, radius)
space.add(body, shape)
pj = pm.PinJoint(space.static_body, body, (300, 425), (0,0))
space.add(pj)
        
fig = plt.figure()
ax = plt.axes(xlim=(0, 600), ylim=(0, 600))
ax.set_aspect("equal")
o = pmplt.DrawOptions(ax)

space.shapes[0].body.apply_impulse_at_local_point((-12000,0))
    
def init():
    space.debug_draw(o)
    return []

steps_per_second = 200
substeps = 10
def animate(dt):
    for x in range(substeps):
        space.step(1/steps_per_second/substeps)
    ax.clear()
    ax.set_xlim(0,600)
    ax.set_ylim(0,600)
    space.debug_draw(o)
    return []

frames = 500
anim = anm.FuncAnimation(fig, animate, init_func=init,
                               frames=frames, interval=20, blit=False, repeat=False)

<IPython.core.display.Javascript object>

Coupled Oscillators

One possible use of Pymunk is to simulate coupled oscillators like the double pendulum. While this system is straightforward to build physically, it can be tricky to reliably start the pendulum in a way that demonstrates the principles you’re covering. Students are frequently first taught the math behind the double pendulum in two dimension, and the focus is usually on the fundamental modes of the system. However, it can be difficult to reliably get the pendulum swinging in a way that demonstrates these principles. It’s very easy to accidentally to start the pendulum in a way that swings in three dimensions, and some of the fundamental modes can require precise angles.

Pymunk can help solve both of these problems. We can simulate a basic double pendulum by modifying our example from above, adding another circle below the first and placing a second PinJoint between them.

%reset -f
# %matplotlib notebook
import matplotlib.pyplot as plt
from matplotlib import animation as anm
import pymunk as pm
from pymunk.vec2d import Vec2d
import pymunk.matplotlib_util as pmplt

space = pm.Space()
space.gravity = (0,-9820)

mass = 10
radius = 25
body1 = pm.Body(mass,pm.moment_for_circle(mass, 0, radius, (0,0)))
body1.position = (300, 375)
# body1.position = (275, 350)
body1.start_position = Vec2d(*body1.position)
shape1 = pm.Circle(body1, radius)
space.add(body1, shape1)
pj1 = pm.PinJoint(space.static_body, body1, (300, 550), (0,0))
space.add(pj1)

mass = 10
radius = 25
body2 = pm.Body(mass,pm.moment_for_circle(mass, 0, radius, (0,0)))
body2.position = (300, 175)
# body2.position = (250, 150)
body2.start_position = Vec2d(*body2.position)
shape2 = pm.Circle(body2, radius)
space.add(body2, shape2)
pj2 = pm.PinJoint(body1, body2, (0,0), (0,0))
space.add(pj2)

        
fig = plt.figure()
ax = plt.axes(xlim=(0, 600), ylim=(0, 600))
ax.set_aspect("equal")
o = pmplt.DrawOptions(ax)

space.shapes[0].body.apply_impulse_at_local_point((-12000,0))
space.shapes[1].body.apply_impulse_at_local_point((20000,0))
    
def init():
    space.debug_draw(o)
    return []

steps_per_second = 100
substeps = 10
def animate(dt):
    for x in range(substeps):
        space.step(1/steps_per_second/substeps)
    ax.clear()
    ax.set_xlim(0,600)
    ax.set_ylim(0,600)
    space.debug_draw(o)
    return []

frames = 1000
anim = anm.FuncAnimation(fig, animate, init_func=init,
                               frames=frames, interval=20, blit=False, repeat=False)

<IPython.core.display.Javascript object>

This is an example of a chaotic system; that is, the exact path that the masses will change dramatically with only a small change to our initial conditions. There are also fundamental modes to this system, in which the pendulum will oscillate in a very predictable manner.

##

Projectile Motion

Next, we’ll simulate a common projectile motion demo that demonstrates the equal pull of gravity on all objects, regardless of their mass. This is sometimes called “Monkey and Hunter”; the premise is that some projectile is being aimed at a target, but the target is released from rest at the same moment that the projectile is being released. However, the person aiming the projectile is aware of this, and wants to know where they should aim to still hit the target. When analyzing this scenario, we find that if the projectile is aimed at the starting location of the target, then the projectile will hit the target.

%reset -f
%matplotlib notebook
import pymunk as pm
from pymunk.vec2d import Vec2d
import matplotlib.pyplot as plt
import pymunk.matplotlib_util as pmplt
from matplotlib import animation as anm

space = pm.Space()
space.gravity = (0,-9800)

mass1 = 10
radius1 = 10
ball1_body = pm.Body(mass=mass1,moment=pm.moment_for_circle(mass1, 0, radius1, (0,0)))
ball1_body.position = (100,100)
ball1_body.start_position = Vec2d(*ball1_body.position)
ball1_body.apply_impulse_at_local_point(Vec2d(17500, 17500))
ball1_shape = pm.Circle(ball1_body,radius1)
space.add(ball1_body,ball1_shape)

mass2 = 50
radius2 = 20
ball2_body = pm.Body(mass=mass2,moment=pm.moment_for_circle(mass2, 0, radius2, (0,0)))
ball2_body.position = (500,500)
ball2_body.start_position = Vec2d(*ball2_body.position)
ball2_shape = pm.Circle(ball2_body,radius2)
space.add(ball2_body,ball2_shape)

fig = plt.figure()
ax = plt.axes(xlim=(0, 600), ylim=(0, 600))
ax.set_aspect("equal")
o = pmplt.DrawOptions(ax)

def init():
    space.debug_draw(o)
    return []

steps_per_second = 200
substeps = 10
def animate(dt):
    for x in range(substeps):
        space.step(1/steps_per_second/substeps)
    ax.clear()
    ax.set_xlim(0,600)
    ax.set_ylim(0,600)
    space.debug_draw(o)
    return []

frames = 50
anim = anm.FuncAnimation(fig, animate, init_func=init,
                               frames=frames, interval=20, blit=False, repeat=False)

<IPython.core.display.Javascript object>

Mass on a Spring

Here, we will demonstrate another constraint object, the damped spring. This is another example of an oscillator, although there are many other demos that can be done using springs. This constraint object works similarly to the previous PinJoint; it connects two objects from user-defined points on those objects and limits how the distance between them can change. However, because springs provide a restoring force instead of simply forcing the objects to stay a fixed difference apart, we must provide some extra parameters to this object. We must define the rest_length (the length of the spring when no force is applied); the stiffness (how much the spring stretches or compresses when a force is applied); and the damping, which will gradually slow our oscillating mass down.

%reset -f
%matplotlib notebook
import pymunk as pm
from pymunk.vec2d import Vec2d
import matplotlib.pyplot as plt
import pymunk.matplotlib_util as pmplt
from matplotlib import animation as anm

space = pm.Space()
# space.gravity = (0,-9000)

mass1 = 10
radius1 = 10
body = pm.Body(mass=mass1,moment=pm.moment_for_circle(mass1, 0, radius1, (0,0)))
body.position = (250,100)
body.start_position = Vec2d(*body.position)
body.apply_impulse_at_local_point(Vec2d(12000, 0))
shape = pm.Circle(body,radius1)
space.add(body,shape)

spring = pm.DampedSpring(space.static_body, body, (50, 100), (0,0), rest_length=200,stiffness=1500,damping=10)
# spring = pm.DampedSpring(space.static_body, body, (50, 100), (0,0), rest_length=200,stiffness=1500,damping=500) # overdamped
space.add(spring)

fig = plt.figure()
ax = plt.axes(xlim=(0, 500), ylim=(0, 200))
ax.set_aspect("equal")
o = pmplt.DrawOptions(ax)
# space.debug_draw(o)
space.shapes[0].body.apply_impulse_at_local_point((5000,0))

def init():
    space.debug_draw(o)
    return []

steps_per_second = 200
substeps = 10
def animate(dt):
    for x in range(substeps):
        space.step(1/steps_per_second/substeps)
    ax.clear()
    ax.set_xlim(0,500)
    ax.set_ylim(0,200)
    space.debug_draw(o)
    return []

frames = 1000
anim = anm.FuncAnimation(fig, animate, init_func=init,
                               frames=frames, interval=20, blit=False, repeat=False)

<IPython.core.display.Javascript object>

By changing the damping value, we can explore undamped systems, as well as underdamping, critical damping, and overdamping.

Key Points

  • The main concepts in pymunk are the space, body, shape and joint

  • Pymunk take charge of the physical simulations leaving the representation to other libraries