The Sieve of Eratosthenes
Overview
Teaching: 45 min
Exercises: 15 minQuestions
How one algorithm looks in 7 different languages?
Objectives
Learn basic syntax from several languages used in scientific computing
Programming Languages for Scientific Computing
There are literally hundreds of programming languages. However, not all of them are suitable or commonly used for Scientific Computing. On this lesson we will present a selection of the most prominent languages for Scientific Computing today.
Without entering in subtle details, we can classify programming languages in several ways, with some shadow zones in between. Programming languages can be:
-
Interpreted or Compiled
-
Static Typed or Dynamic Typed.
In general compiled languages are also static typed and interpreted languages are dynamically typed. Examples of compiled languages are C/C++ and Fortran, in the category of interpreted we can mention Python, R and Julia. Java is an special case where code is compiled in a intermediate representation called “bytecode” that is interpreted by the Java Virtual Machine during execution.
The difference is even more diffuse by technologies like Just-in-Time compilation that uses compilation during runtime for an usually interpreted language.
There are only 3 languages that we can consider as truly High-Performance Programming Languages (PL), this trinity is made by Fortran, C and C++. Other languages, like Python and R even if used very often in Scientific Computing are not High-Performance at its core. Julia is a newer language filling the gap in this classification.
Fortran, C and C++ are all of them static typed, compiled and the most prominent paradigms for Parallel Computing in CPUs OpenMP and MPI has official support for those 3 languages. Among the list of languages that we will consider today they are also the older ones.
The next table shows the age of several languages used in Scientific Computing.
The Age of Programming Languages (by 2018)
Language First appeared Stable Release Fortran 1957; 61 years ago Fortran 2008 (ISO/IEC 1539-1:2010) / 2010; 8 years ago C 1972; 46 years ago C11 / December 2011; 6 years ago C++ 1985; 33 years ago ISO/IEC 14882:2017 / 1 December 2017; 7 months ago Python 1990; 27 years ago 3.7.0 / 27 June 2018; 2.7.15 / 1 May 2018 R 1993; 24 years ago 3.5.1 (“Feather Spray”)/ July 2, 2018 Java 1995; 23 years ago Java 10, released on March 20, 2018 Julia 2012; 6 years ago 0.6.4 / 9 July 2018
More about programming languages
The figure above was found on this Blog: Languages you should know
The Sieve of Eratosthenes
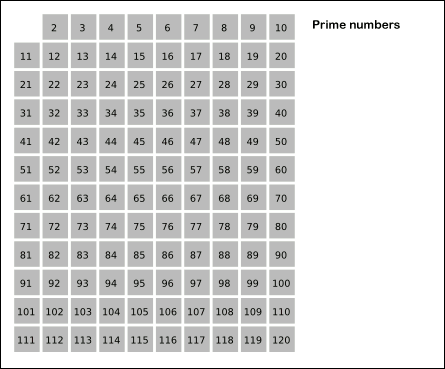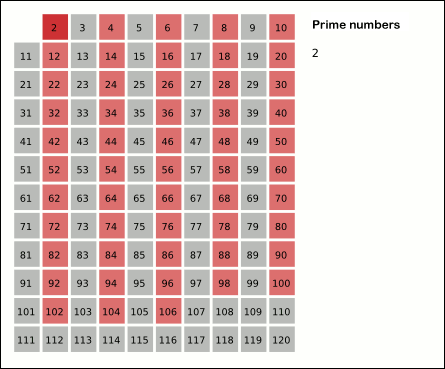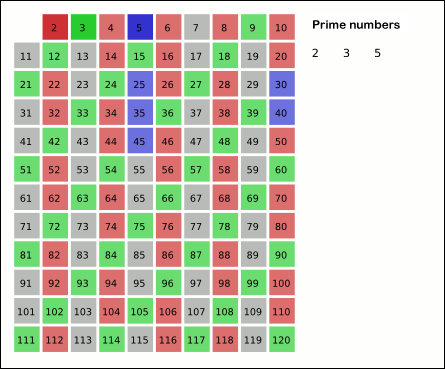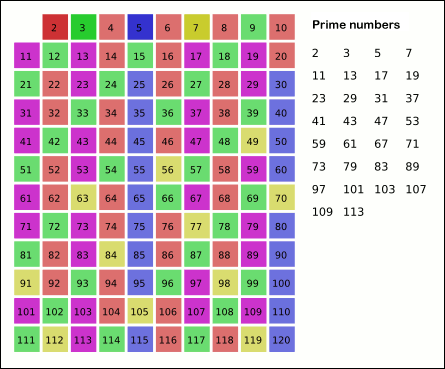
In order to illustrate all those languages in a short glimpse we will be showing how to implement the same algorithm in all those 7 languages. The algorithm is called the Sieve of Eratosthenes and it is a classical algorithm for finding all prime numbers up to any given limit. These are the rules for the implementation.
-
All implementations will be as close as possible to each other. In fact, that is a bad idea from the performance point of view but, for our purpose will facilitate the comparison in syntax rather how to achieve top performance with each PL.
-
No external libraries will be used, with the sole exception of Input/Output routines. Interpreted languages take advantage of external libraries to improve performance, those external languages are usually written in a compiled language, that is the case of several R and Python libraries.
-
The fairly accelerate the algorithm we will skip all even numbers, there is just one prime even number and we know what it is.
For this exercises, please enter in interactive mode as the head node cannot take all users executing at the same time. The Sieve was chosen for being very CPU intensive but with little memory requirements.
R
Lets start with interpreted languages. R is one of the most used languages for statistical analysis. The sieve here is implemented as an Rscript and uses a full dimension for the array. It expects one integer argument as the upper limit for the sieve, otherwise defaults to 100.
#!/usr/bin/env Rscript
SieveOfEratosthenes <- function(n) {
if (n < 2) return(NULL)
primes <- rep(T, n)
sprintf(" Dimension of array %d", length(primes))
# 1 is not prime
primes[1] <- F
for(i in seq(n)) {
if (primes[i]) {
j <- i * i
if (j > n){
if (sum(primes, na.rm=TRUE)<10000) {
# Select just the indices of True values
print(which(primes))
}
return(sum(primes, na.rm=TRUE))
}
primes[seq(j, n, by=i)] <- F
}
}
return()
}
# Collecting arguments from the command
args = commandArgs(trailingOnly=TRUE)
# Default number is n=100
if (length(args)==0) {
n = 100
} else {
n = strtoi(args[1])
}
sprintf(" Prime numbers up to %d", n)
nprimes<-SieveOfEratosthenes(n)
sprintf(" Total number of primes found: %d", nprimes)
Now lets get some timing on how much it takes for the first 100 million integers. This timing was taking on Spruce but your numbers could be different based on which compute node are you running.
$ time ./SieveOfEratosthenes.R 100000000
[1] " Prime numbers up to 100000000"
[1] " Total number of primes found: 5761455"
real 0m24.492s
user 0m23.672s
sys 0m0.823s
Python
Our second interpreted language is Python, the implementation below is not using numpy, the numerical library. This is big handicap for this implementation having to rely only on very flexible but efficient python lists. Lists are part of the core language. Numpy, even not being part of the core or even the standard library is the defacto standard for manipulate arrays as we will see later today.
#!/usr/bin/env python3
import sys
def SieveOfEratosthenes(n):
if n%2 == 0:
imax=int(n/2)
else:
imax=int((n+1)/2)
neff= 2*(imax-1)+1
prime = imax*[True]
print(" Dimension of array: %d\n" % imax)
print(" Array with indices between 0 to %d\n" % (imax-1))
print(" Stores primality of odd numbers in range [1, %d]\n\n" % neff)
# The loop runs over all odd numbers starting at 3
p=3
while (p<n/2+1):
# If prime[p] is true, then it is a prime
if(prime[int((p-1)/2)] == 1):
# Update all multiples of p
i = 2*p
while (i <= neff):
if (i%2!=0):
prime[int((i-1)/2)] = False
i += p
p+=2
counter = 1
nprimes = 0
# Print all prime numbers if the number is small otherwise just count the number of primes found
if (imax < 10000):
print("%8d " % 2, end='')
# Starting with index 1 instead of zero because (2*0)+1 = 1 is not prime
for i in range(1,imax):
if(prime[i] == 1):
print("%8d " % (2*i+1), end='')
counter+=1
if (counter == 15):
print("")
counter=0
print("\n")
for i in range(1,imax):
if(prime[i] is True):
nprimes+=1
return nprimes + 1
if __name__ == "__main__":
if (len(sys.argv) > 1):
n = int(sys.argv[1])
else:
n = 100
print("")
print(" Prime numbers up to %d" % n)
nprimes = SieveOfEratosthenes(n)
print(" Total number of primes found: %d" % nprimes)
And the timing (Obs: it is very slow!), so be patient
$ time ./SieveOfEratosthenes.py 100000000
Prime numbers up to 100000000
Dimension of array: 50000000
Array with indices between 0 to 49999999
Stores primality of odd numbers in range [1, 99999999]
Total number of primes found: 5761455
real 1m21.595s
user 1m21.505s
sys 0m0.111s
Java
The big advantage of Java is being able to run with the same bytecode on machines running different Operating Systems like Linux and Windows. There are a number of scientific packages written in Java and packages for Data Analysis
class SieveOfEratosthenes
{
void sieveOfEratosthenes(int n)
{
// Create a boolean array, we will avoid all even numbers
// so the element i on the array stores true or false if
// the number 2*i+1 is actually prime
int imax, neff, counter=1, nprimes=0;
boolean prime[];
if (n%2==0)
imax=n/2;
else
imax=(n+1)/2;
neff= 2*(imax-1)+1;
prime = new boolean[imax];
// Lets assume that all odd numbers are primes
for(int i=0;i<imax;i++)
prime[i] = true;
System.out.format(" Dimension of array: %d\n", imax);
System.out.format(" Array with indices between 0 to %d\n", imax-1);
System.out.format(" Stores primality of odd numbers in range [1, %d]\n\n", neff);
// The loop runs over all odd numbers starting at 3
for(int p = 3; p <n/2+1; p+=2)
{
// If prime[p] is true, then it is a prime
if(prime[(p-1)/2] == true)
{
// Update all multiples of p
for(int i = p*2; i <= neff; i += p)
{
if (i%2!=0) prime[(i-1)/2] = false;
}
}
}
// Print all prime numbers if the number is small otherwise just count the number of primes found
if (imax < 10000) {
System.out.format("%8d ", 2);
// Starting with index 1 instead of zero because (2*0)+1 = 1 is not prime
for(int i = 1; i < imax; i++){
if(prime[i] == true){
System.out.format("%8d ", 2*i+1);
counter++;
}
if (counter == 15){
System.out.format("\n");
counter=0;
}
}
System.out.format("\n");
}
else {
for(int i = 1; i < imax; i++){
if(prime[i] == true)
nprimes ++;
}
System.out.format(" Total number of primes found: %d\n", nprimes+1);
}
}
// Main program, reads command line to get upper limit for Sieve
public static void main(String args[])
{
int n=1;
if (args.length > 0) {
try {
n = Integer.parseInt(args[0]);
} catch (NumberFormatException e) {
System.err.println("Argument" + args[0] + " must be an integer.");
System.exit(1);
}
}
else
n = 100;
System.out.format("\n");
System.out.format(" Prime numbers up to %d\n", n);
SieveOfEratosthenes g = new SieveOfEratosthenes();
g.sieveOfEratosthenes(n);
}
}
We need to compile the Java code in what is called “bytecode”. That is different from “machine code”. The resulting file has the “.class” extension and is interpreted by the Java Virtual Machine. The same “.class” file can run exactly as it is on another machine.
Load the corresponding module for Java JDK and compile the sources as follows:
$ module load compilers/java/jdk1.8.0
$ javac SieveOfEratosthenes.java
To execute, notice that the extension “.class” is not added on the command line. The java interpreter (JVM) assumes that extension
$ time java SieveOfEratosthenes 100000000
Prime numbers up to 100000000
Dimension of array: 50000000
Array with indices between 0 to 49999999
Stores primality of odd numbers in range [1, 99999999]
Total number of primes found: 5761455
real 0m1.137s
user 0m1.132s
sys 0m0.049s
C
C is a compiled language frequently used as the standard language to write operating systems. It is general purpose in contrast to Fortran that is specific for numerical computing.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int sieveOfEratosthenes(unsigned int n);
int main(int argc, char *argv[])
{
unsigned int n=1, nprimes;
if (argc > 1) n = atoi(argv[1]);
else n = 100;
printf(" Prime numbers up to %d\n", n);
nprimes=sieveOfEratosthenes(n);
printf(" Total number of primes found: %d\n\n", nprimes);
}
int sieveOfEratosthenes(unsigned int n)
{
unsigned int imax, neff, counter=1, nprimes=0;
char *prime;
if (n%2==0)
imax=n/2;
else
imax=(n+1)/2;
neff= 2*(imax-1)+1;
prime = (char *)malloc(imax * sizeof(char));
for(unsigned int i=0; i<imax; i++){
prime[i]=1;
}
printf(" Dimension of array: %d\n", imax);
printf(" Array with indices between 0 to %d\n", imax-1);
printf(" Stores primality of odd numbers in range [1, %d]\n\n", neff);
// The loop runs over all odd numbers starting at 3
for(unsigned int p = 3; p <n/2+1; p+=2)
{
// If prime[p] is true, then it is a prime
if(prime[(p-1)/2] == 1)
{
// Update all multiples of p
for(unsigned int i = p*2; i <= neff; i += p)
{
if (i%2!=0) prime[(i-1)/2] = 0;
}
}
}
// Print all prime numbers if the number is small otherwise just count the number of primes found
if (imax < 10000) {
printf("%10d ", 2);
// Starting with index 1 instead of zero because (2*0)+1 = 1 is not prime
for(unsigned int i = 1; i < imax; i++){
if(prime[i] == 1){
printf("%10d ", 2*i+1);
counter++;
}
if (counter == 15){
printf("\n");
counter=0;
}
}
printf("\n");
}
for(unsigned int i = 1; i < imax; i++){
if(prime[i] == true)
nprimes ++;
}
// Adding one extra due to 2 that is not counted on the list
return nprimes+1;
}
Lets do a simple compilation and timing
$ gcc SieveOfEratosthenes.cxx
$ time ./a.out 100000000
Prime numbers up to 100000000
Dimension of array: 50000000
Array with indices between 0 to 49999999
Stores primality of odd numbers in range [1, 99999999]
Total number of primes found: 5761455
real 0m4.571s
user 0m4.560s
sys 0m0.011s
C++
C++ originally was created very close to C but offering Object-Oriented Programming that C due to its age never had. Nowadays C++ have departed significantly from C, C code for most part still compiles on a C++ compiler but the language itself have grown in complexity, specially with the latest specifications, C++11 and C++14.
#include <inttypes.h>
#include <limits>
#include <cmath>
#include <sstream>
#include <iostream>
#include <iomanip>
#include <algorithm>
#include <vector>
template <typename ForwardIterator>
size_t SieveOfEratosthenes(ForwardIterator start, ForwardIterator end)
{
if (start == end) return 0;
// Filling the entire vector with zeros
std::fill(start, end, 0);
// mark composites with 1
for (ForwardIterator prime_it = start + 1; prime_it != end; ++prime_it)
{
if (*prime_it == 1) continue;
// The variable stride contains the actual prime number that we use to skip across
size_t stride = (prime_it - start) + 1;
// Jumping with stride all elements staring on the current index are marked as non-primes
ForwardIterator mark_it = prime_it;
while ((end - mark_it) > stride)
{
std::advance(mark_it, stride);
// Here is where the non-prime is marked
*mark_it = 1;
}
}
// copy marked primes into container
ForwardIterator out_it = start;
for (ForwardIterator it = start + 1; it != end; ++it)
{
if (*it == 0)
{
*out_it = (it - start) + 1;
++out_it;
}
}
return out_it - start;
}
int main(int argc, const char* argv[])
{
using namespace std;
int n=100, counter=0;
if (argc == 2) {
stringstream ss(argv[--argc]);
ss >> n;
if (n < 1 or ss.fail()) {
cerr << "USAGE:\n SieveOfEratosthenes N\n\nwhere N in the range [1, "
<< numeric_limits<int>::max() << ")" << endl;
return 2;
}
}
std::vector<int> primes(n);
printf(" Prime numbers up to %d\n", n);
size_t nprimes = SieveOfEratosthenes(primes.begin(), primes.end());
if (n <= 10000){
for (size_t i = 0; i < nprimes; ++i)
{
std::cout << std::setw(8) << primes[i] << " ";
counter++;
if (counter==10){
counter = 0;
std::cout << std::endl;
}
}
std::cout << std::endl;
}
std::cout << " Total number of primes found: "<< nprimes<< std::endl;
return 0;
}
The implementation uses vector that is part of the Standard Library. The timing follows:
$ g++ SieveOfEratosthenes.cpp
$ time ./a.out 100000000
Prime numbers up to 100000000
Total number of primes found: 5761455
real 0m21.324s
user 0m21.240s
sys 0m0.091s
Fortran
Fortran is one of the oldest programming languages. It was created to do numerical computations from the very beginning. It have evolved with time from the strict format of Fotran 77 into a modern language that includes modules but still having a appeal for numerical computing. Together with C and C++ constitutes the triad of truly HPC languages.
subroutine SieveOfEratosthenes(n, nprimes)
implicit none
integer, intent(in) :: n
integer, intent(out) :: nprimes
integer :: imax, neff, counter=1
integer, allocatable :: prime(:)
integer :: i,p
if ( mod(n,2) .eq. 0) then
imax=n/2
else
imax=(n+1)/2
end if
neff= 2*(imax-1)+1
allocate(prime(0:imax))
do i=0, imax
prime(i)=1
end do
write(*,*) " Dimension of array: ", imax
write(*,*) " Array with indices between 0 to ", imax-1
write(*,'(1X,A,I0,A,A)') " Stores primality of odd numbers in range [1,", neff, "]", char(0)
! The loop runs over all odd numbers starting at 3
do p = 3, n/2+1, 2
! If prime(p) is 1, then it is a prime
if(prime((p-1)/2) == 1) then
! Update all multiples of p
do i = p*2, neff, p
if (mod(i,2)/=0) then
prime((i-1)/2) = 0
end if
end do
end if
end do
! Print all prime numbers if the number is small otherwise just count the number of primes found
if (imax < 10000) then
write(*,'(I10)', advance="no") 2
! Starting with index 1 instead of zero because (2*0)+1 = 1 is not prime
do i = 1, imax, 1
if(prime(i) == 1) then
write(*,'(I10)', advance="no") 2*i+1
counter = counter + 1
end if
if (counter == 15) then
write(*,*) char(0)
counter=0
end if
end do
write(*,*) char(0)
end if
do i = 1, imax, 1
if(prime(i) == 1) then
nprimes = nprimes + 1
end if
end do
end subroutine SieveOfEratosthenes
program main
implicit none
integer :: n=1, nprimes, count, stat
character(len=32) :: arg
count = command_argument_count()
! print *, count
if (count > 0) then
CALL get_command_argument(1, arg)
read(arg,*,iostat=stat) n
else
n = 100
end if
write(*,*) char(0)
write(*,*) " Prime numbers up to ", n
call SieveOfEratosthenes(n, nprimes)
write(*,*) " Total number of primes found: ", nprimes
end program main
$ gfortran SieveOfEratosthenes.f90
$ time ./a.out 100000000
Prime numbers up to 100000000
Dimension of array: 50000000
Array with indices between 0 to 49999999
Stores primality of odd numbers in range [1,99999999]
Total number of primes found: 5761455
real 0m6.779s
user 0m6.733s
sys 0m0.049s
Julia
Our last programming language is Julia. A modern interpreted language that performs very similar to a compiled language. It offers a lot of modern syntax as we can see from this implementation.
function SieveOfEratosthenes(lim :: Int)
is_prime :: Array = trues(lim)
llim :: Int = isqrt(lim)
result :: Array = [2] #Initial array
for i = 3:2:lim
if is_prime[i]
if i <= llim
for j = i*i:2*i:lim
is_prime[j] = false
end
end
push!(result,i)
end
end
return result
end
n=parse(Int64,ARGS[1])
println("Prime numbers up to " * string(n))
ret=SieveOfEratosthenes(n)
if (size(ret,1)<1000)
println(ret)
end
println("Total number of primes found: " * string(size(ret,1)))
And the timing
$ time julia SieveOfEratosthenes.jl 100000000
Prime numbers up to 100000000
Total number of primes found: 5761455
real 0m1.444s
user 0m1.456s
sys 0m1.297s
Wrapping up
There are a number of programming languages used in Scientific Computing. We have shown a selection of 7 languages with open implementations. This exercise was intended to expose the way each code is compiled and executed. A benchmark is only illustrative of the performance of each language, with the premise that we have avoided the use of external libraries. The table below shows the timings obtained on Spruce by the time this was written.
| Programming Language | Time to compute primes up to 1E8 |
|---|---|
| R | 24.4 s |
| Python | 81.5 s |
| Java | 1.1 s |
| C | 4.5 s |
| C++ | 21.3 s |
| Fortran | 6.7 s |
| Julia | 1.4 s |
In the case of C, C++ and Fortran, no optimization options were used during compilation. The table below shows the timings compiling with optimization option level 3 -O3 and using GCC compilers gcc, g++ and gfortran
| Programming Language | Time to compute primes up to 1E8 |
|---|---|
| C | 0.947 s |
| C++ | 2.661 s |
| Fortran | 1.242 s |
Key Points
A literal translation of an algorithm ends up in a poorly efficient code.
Each language has its own way of doing things. Knowing how to adapt the algorithm to the language is the way to create efficient code.
